
Identify the two modified Lagrange equations and solve for
Answer to Problem 7.50P
Modified Lagrangian equations are
Explanation of Solution
Draw the diagram of given arrangement.
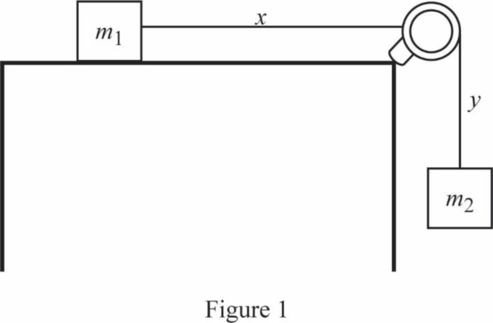
Write the equation for the kinetic energy of the system.
Here,
Assume the potential energy at the height of table is zero. The only potential energy is due to the gravity.
Write the equation for the Lagrangian of the system.
Rewrite the above equation by substituting the previous two equations.
Write the Euler-Lagrange equation with constraints.
Here,
Write the two modified Lagrange equations.
Write the constraint equation.
Differentiate the above function with respect to x.
Differentiate
Differentiate equation (I) with respect to x.
Differentiate equation (I) with respect to y.
Differentiate equation (I) with respect to
Differentiate the above equation with respect to t.
Differentiate equation (I) with respect to
Differentiate the above equation with respect to t.
Rewrite equation (II) by substituting equations (VI) and (VIII).
Rewrite equation (III) by substituting equations (VII) and (IX).
The function
Substitute
Substitute the above equation in
Rewrite the equation
Substitute
Thus, the required equations are
Write the equation for force on string from equation 7.122.
Write the expression for constraint forces associated with the tension on string.
Thus, the
Rewrite the equation
Rewrite the above equation by substituting
Thus, the magnitude of tension on mass
Substitute 1 for
Rewrite the above equation by substituting
Thus, the magnitude of tension on mass
Draw the free body diagram of the system.
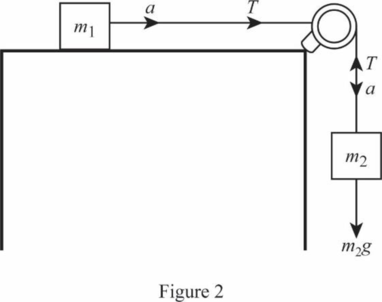
Write the Newton’s equation for net force.
Here,
Write the equation for net horizontal force on mass
Here,
Write the Newton’s equation for mass
Equate the right-hand sides of above two equations.
Write the net vertical force on mass
Write the Newton’s equation for mass
Equate the right-hand sides of above two equations.
Substitute
Substitute the above equation in
The result is same that of obtained from modified Lagrangian equations.
Thus, the modified Lagrangian equations are
Want to see more full solutions like this?
Chapter 7 Solutions
Classical Mechanics
 College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781305952300Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON
University Physics (14th Edition)PhysicsISBN:9780133969290Author:Hugh D. Young, Roger A. FreedmanPublisher:PEARSON Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press
Introduction To Quantum MechanicsPhysicsISBN:9781107189638Author:Griffiths, David J., Schroeter, Darrell F.Publisher:Cambridge University Press Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and EngineersPhysicsISBN:9781337553278Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley
Lecture- Tutorials for Introductory AstronomyPhysicsISBN:9780321820464Author:Edward E. Prather, Tim P. Slater, Jeff P. Adams, Gina BrissendenPublisher:Addison-Wesley College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON
College Physics: A Strategic Approach (4th Editio...PhysicsISBN:9780134609034Author:Randall D. Knight (Professor Emeritus), Brian Jones, Stuart FieldPublisher:PEARSON





