
Calculus (MindTap Course List)
11th Edition
ISBN: 9781337275347
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 8.8, Problem 15E
Evaluating an Improper
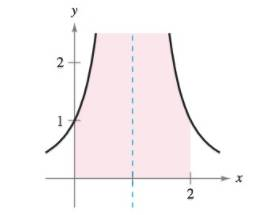
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Using the integral definition, transform the sum into an integral and find the answer.
(CALCULUS 2: IMPROPER INTEGRALS)
Determine all values of p for which the integral is improper.
Evaluating an Improper Integral :- , Determine whether the improper integral diverges or converges. Evaluate the integral if it converges :-
See the equation as attached here
Chapter 8 Solutions
Calculus (MindTap Course List)
Ch. 8.1 - Integration Technique Describe how to integrate a...Ch. 8.1 - Prob. 2ECh. 8.1 - Choosing an Antiderivative In Exercises 3 and 4,...Ch. 8.1 - Choosing an Antiderivative In Exercises 3 and 4,...Ch. 8.1 - Choosing a Formula In Exercises 514, select the...Ch. 8.1 - Prob. 6ECh. 8.1 - Choosing a Formula In Exercises 514, select the...Ch. 8.1 - Prob. 8ECh. 8.1 - Prob. 9ECh. 8.1 - Prob. 10E
Ch. 8.1 - Choosing a Formula In Exercises 514, select the...Ch. 8.1 - Prob. 12ECh. 8.1 - Choosing a Formula In Exercises 514, select the...Ch. 8.1 - Prob. 14ECh. 8.1 - Prob. 15ECh. 8.1 - Prob. 16ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 19ECh. 8.1 - Prob. 20ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 22ECh. 8.1 - Prob. 23ECh. 8.1 - Prob. 24ECh. 8.1 - Prob. 25ECh. 8.1 - Prob. 26ECh. 8.1 - Prob. 27ECh. 8.1 - Prob. 28ECh. 8.1 - Prob. 29ECh. 8.1 - Prob. 30ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 32ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 34ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 36ECh. 8.1 - Prob. 37ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 41ECh. 8.1 - Prob. 42ECh. 8.1 - Finding an indefinite Integral In Exercises 1546,...Ch. 8.1 - Prob. 44ECh. 8.1 - Prob. 45ECh. 8.1 - Prob. 46ECh. 8.1 - Slope Field In Exercises 47 and 48, a differential...Ch. 8.1 - Prob. 48ECh. 8.1 - Prob. 49ECh. 8.1 - Prob. 50ECh. 8.1 - Prob. 51ECh. 8.1 - Prob. 52ECh. 8.1 - Prob. 53ECh. 8.1 - Prob. 54ECh. 8.1 - Prob. 55ECh. 8.1 - Prob. 56ECh. 8.1 - Evaluating a Definite Integral In Exercises 57-72,...Ch. 8.1 - Prob. 58ECh. 8.1 - Prob. 59ECh. 8.1 - Prob. 60ECh. 8.1 - Evaluating a Definite Integral In Exercises 57-72,...Ch. 8.1 - Prob. 62ECh. 8.1 - Prob. 63ECh. 8.1 - Prob. 64ECh. 8.1 - Prob. 65ECh. 8.1 - Prob. 66ECh. 8.1 - Prob. 67ECh. 8.1 - Prob. 68ECh. 8.1 - Evaluating a Definite Integral In Exercises 57-72,...Ch. 8.1 - Prob. 70ECh. 8.1 - Prob. 71ECh. 8.1 - Prob. 72ECh. 8.1 - Area In Exercises 7376, find the area of the given...Ch. 8.1 - Prob. 74ECh. 8.1 - Prob. 75ECh. 8.1 - Prob. 76ECh. 8.1 - Prob. 77ECh. 8.1 - Prob. 78ECh. 8.1 - Prob. 79ECh. 8.1 - Prob. 80ECh. 8.1 - Prob. 81ECh. 8.1 - Prob. 82ECh. 8.1 - Prob. 83ECh. 8.1 - Prob. 84ECh. 8.1 - Comparing Antiderivatives (a) Explain why the...Ch. 8.1 - Prob. 86ECh. 8.1 - Prob. 87ECh. 8.1 - Prob. 88ECh. 8.1 - Prob. 89ECh. 8.1 - Prob. 90ECh. 8.1 - Prob. 91ECh. 8.1 - Prob. 92ECh. 8.1 - Prob. 93ECh. 8.1 - Prob. 94ECh. 8.1 - Prob. 95ECh. 8.1 - Prob. 96ECh. 8.1 - Prob. 97ECh. 8.1 - Prob. 98ECh. 8.1 - Prob. 99ECh. 8.1 - Prob. 100ECh. 8.1 - Finding a Pattern (a) Find cos3xdx. (b) Find...Ch. 8.1 - Prob. 102ECh. 8.1 - Prob. 103ECh. 8.1 - Prob. 104ECh. 8.2 - CONCEPT CHECK Integration by Parts Integration by...Ch. 8.2 - Prob. 2ECh. 8.2 - Prob. 3ECh. 8.2 - Prob. 4ECh. 8.2 - Prob. 5ECh. 8.2 - Setting Up Integration by Parts In Exercises 510,...Ch. 8.2 - Prob. 7ECh. 8.2 - Prob. 8ECh. 8.2 - Prob. 9ECh. 8.2 - Prob. 10ECh. 8.2 - Prob. 11ECh. 8.2 - Using Integration by Parts In Exercises 11-14,...Ch. 8.2 - Prob. 13ECh. 8.2 - Using Integration by Parts In Exercises 11-14,...Ch. 8.2 - Prob. 15ECh. 8.2 - Prob. 16ECh. 8.2 - Prob. 17ECh. 8.2 - Prob. 18ECh. 8.2 - Finding an Indefinite Integral In Exercises 1534,...Ch. 8.2 - Finding an Indefinite Integral In Exercises 1534,...Ch. 8.2 - Prob. 21ECh. 8.2 - Prob. 22ECh. 8.2 - Prob. 23ECh. 8.2 - Finding an Indefinite Integral In Exercises 15-34,...Ch. 8.2 - Prob. 25ECh. 8.2 - Prob. 26ECh. 8.2 - Finding an Indefinite Integral In Exercises 1534,...Ch. 8.2 - Finding an Indefinite Integral In Exercises 15-34,...Ch. 8.2 - Prob. 29ECh. 8.2 - Prob. 30ECh. 8.2 - Prob. 31ECh. 8.2 - Prob. 32ECh. 8.2 - Prob. 33ECh. 8.2 - Prob. 34ECh. 8.2 - Prob. 35ECh. 8.2 - Prob. 36ECh. 8.2 - Prob. 37ECh. 8.2 - Prob. 38ECh. 8.2 - Prob. 39ECh. 8.2 - Prob. 40ECh. 8.2 - Prob. 41ECh. 8.2 - Prob. 42ECh. 8.2 - Prob. 43ECh. 8.2 - Prob. 44ECh. 8.2 - Prob. 45ECh. 8.2 - Prob. 46ECh. 8.2 - Prob. 47ECh. 8.2 - Evaluating a Definite Integral In Exercises 43-52,...Ch. 8.2 - Prob. 49ECh. 8.2 - Prob. 50ECh. 8.2 - Evaluating a Definite Integral In Exercises 4352,...Ch. 8.2 - Evaluating a Definite Integral In Exercises 4352,...Ch. 8.2 - Prob. 53ECh. 8.2 - Prob. 54ECh. 8.2 - Prob. 55ECh. 8.2 - Prob. 56ECh. 8.2 - Prob. 57ECh. 8.2 - Prob. 58ECh. 8.2 - Prob. 59ECh. 8.2 - Prob. 60ECh. 8.2 - Integration by Parts State whether you would use...Ch. 8.2 - Prob. 62ECh. 8.2 - Prob. 63ECh. 8.2 - Prob. 64ECh. 8.2 - Prob. 65ECh. 8.2 - Prob. 66ECh. 8.2 - Prob. 67ECh. 8.2 - Prob. 68ECh. 8.2 - Prob. 69ECh. 8.2 - Finding a General Rule In Exercises 69 and 70, use...Ch. 8.2 - Prob. 71ECh. 8.2 - Prob. 72ECh. 8.2 - Prob. 73ECh. 8.2 - Prob. 74ECh. 8.2 - Prob. 75ECh. 8.2 - Prob. 76ECh. 8.2 - Prob. 77ECh. 8.2 - Prob. 78ECh. 8.2 - Prob. 79ECh. 8.2 - Prob. 80ECh. 8.2 - Prob. 81ECh. 8.2 - Prob. 82ECh. 8.2 - Area In Exercises 83-86, use a graphing utility to...Ch. 8.2 - Prob. 84ECh. 8.2 - Area In Exercises 83-86, use a graphing utility to...Ch. 8.2 - Prob. 86ECh. 8.2 - Prob. 87ECh. 8.2 - Prob. 88ECh. 8.2 - Prob. 89ECh. 8.2 - Prob. 90ECh. 8.2 - Prob. 91ECh. 8.2 - Prob. 92ECh. 8.2 - Prob. 93ECh. 8.2 - Prob. 94ECh. 8.2 - Prob. 95ECh. 8.2 - Prob. 96ECh. 8.2 - Prob. 97ECh. 8.2 - Prob. 98ECh. 8.2 - Finding an Error Find the fallacy in the following...Ch. 8.2 - Find a real number c and a positive number L for...Ch. 8.3 - CONCEPT CHECK Analyzing Indefinite Integrals Which...Ch. 8.3 - Prob. 2ECh. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Prob. 8ECh. 8.3 - Prob. 9ECh. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Finding an Indefinite Integral Involving Sine and...Ch. 8.3 - Prob. 12ECh. 8.3 - Prob. 13ECh. 8.3 - Prob. 14ECh. 8.3 - Using Wallis's Formulas In Exercises 15-20, use...Ch. 8.3 - Using Wallis's Formulas In Exercises 15-20, use...Ch. 8.3 - Using Wallis's Formulas In Exercises 15-20, use...Ch. 8.3 - Using Wallis's Formulas In Exercises 15-20, use...Ch. 8.3 - Using Wallis's Formulas In Exercises 15-20, use...Ch. 8.3 - Using Wallis's Formulas In Exercises 15-20, use...Ch. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Prob. 26ECh. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Prob. 28ECh. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Prob. 30ECh. 8.3 - Prob. 31ECh. 8.3 - Prob. 32ECh. 8.3 - Finding an Indefinite Integral Involving Secant...Ch. 8.3 - Prob. 34ECh. 8.3 - Prob. 35ECh. 8.3 - Prob. 36ECh. 8.3 - Differential Equation In Exercises 35-38, find the...Ch. 8.3 - Prob. 38ECh. 8.3 - Prob. 39ECh. 8.3 - Prob. 40ECh. 8.3 - Slope Field In Exercises 41 and 42, use a computer...Ch. 8.3 - Prob. 42ECh. 8.3 - Using a Product-to-Sum Formula In Exercises 43-48,...Ch. 8.3 - Prob. 44ECh. 8.3 - Prob. 45ECh. 8.3 - Prob. 46ECh. 8.3 - Using a Product-to-Sum Formula In Exercises 43-48,...Ch. 8.3 - Prob. 48ECh. 8.3 - Prob. 49ECh. 8.3 - Prob. 50ECh. 8.3 - Prob. 51ECh. 8.3 - Prob. 52ECh. 8.3 - Prob. 53ECh. 8.3 - Finding an Indefinite Integral In Exercises 4958,...Ch. 8.3 - Finding an Indefinite Integral In Exercises 49-58,...Ch. 8.3 - Prob. 56ECh. 8.3 - Prob. 57ECh. 8.3 - Prob. 58ECh. 8.3 - Prob. 59ECh. 8.3 - Prob. 60ECh. 8.3 - Prob. 61ECh. 8.3 - Prob. 62ECh. 8.3 - Prob. 63ECh. 8.3 - Prob. 64ECh. 8.3 - Prob. 65ECh. 8.3 - Prob. 66ECh. 8.3 - Prob. 67ECh. 8.3 - Prob. 68ECh. 8.3 - Prob. 69ECh. 8.3 - Prob. 70ECh. 8.3 - Prob. 71ECh. 8.3 - Prob. 72ECh. 8.3 - Prob. 73ECh. 8.3 - Prob. 74ECh. 8.3 - Prob. 75ECh. 8.3 - Prob. 76ECh. 8.3 - Volume and Centriod In Exercises 77 and 78, for...Ch. 8.3 - Prob. 78ECh. 8.3 - Prob. 79ECh. 8.3 - Verifying a Reduction Formula In Exercises 79-82,...Ch. 8.3 - Prob. 81ECh. 8.3 - Prob. 82ECh. 8.3 - Prob. 83ECh. 8.3 - Prob. 84ECh. 8.3 - Prob. 85ECh. 8.3 - Prob. 86ECh. 8.3 - Prob. 87ECh. 8.3 - Prob. 88ECh. 8.3 - Prob. 89ECh. 8.4 - CONCEPT CHECK Trigonometric Substitution State the...Ch. 8.4 - Prob. 2ECh. 8.4 - Prob. 3ECh. 8.4 - Prob. 4ECh. 8.4 - Using trigonometric Substitution In Exercises 36,...Ch. 8.4 - Using trigonometric Substitution In Exercises 36,...Ch. 8.4 - Prob. 7ECh. 8.4 - Prob. 8ECh. 8.4 - Using Trigonometric Substitution In Exercises 710,...Ch. 8.4 - Prob. 10ECh. 8.4 - Prob. 11ECh. 8.4 - Prob. 12ECh. 8.4 - Prob. 13ECh. 8.4 - Prob. 14ECh. 8.4 - Prob. 15ECh. 8.4 - Prob. 16ECh. 8.4 - Prob. 17ECh. 8.4 - Special Integration Formulas In Exercises 1518,...Ch. 8.4 - Prob. 19ECh. 8.4 - Prob. 20ECh. 8.4 - Prob. 21ECh. 8.4 - Prob. 22ECh. 8.4 - Finding an Indefinite Integral In Exercises 19-32,...Ch. 8.4 - Finding an Indefinite Integral In Exercises 19-32,...Ch. 8.4 - Prob. 25ECh. 8.4 - Prob. 26ECh. 8.4 - Prob. 27ECh. 8.4 - Prob. 28ECh. 8.4 - Prob. 29ECh. 8.4 - Prob. 30ECh. 8.4 - Prob. 31ECh. 8.4 - Prob. 32ECh. 8.4 - Prob. 33ECh. 8.4 - Prob. 34ECh. 8.4 - Prob. 35ECh. 8.4 - Prob. 36ECh. 8.4 - Prob. 37ECh. 8.4 - Prob. 38ECh. 8.4 - Prob. 39ECh. 8.4 - Prob. 40ECh. 8.4 - Prob. 41ECh. 8.4 - Prob. 42ECh. 8.4 - Prob. 43ECh. 8.4 - Prob. 44ECh. 8.4 - Comparing Methods (a) Find the integral x1x2dx...Ch. 8.4 - Prob. 46ECh. 8.4 - Prob. 47ECh. 8.4 - True or False? In Exercises 47-50, determine...Ch. 8.4 - Prob. 49ECh. 8.4 - Prob. 50ECh. 8.4 - Prob. 51ECh. 8.4 - Prob. 52ECh. 8.4 - Prob. 53ECh. 8.4 - Prob. 54ECh. 8.4 - Volume of a Torus In Exercises 55 and 56, find the...Ch. 8.4 - Prob. 56ECh. 8.4 - Prob. 57ECh. 8.4 - Prob. 58ECh. 8.4 - Prob. 59ECh. 8.4 - Prob. 60ECh. 8.4 - Tractrix A person moves from the origin along the...Ch. 8.4 - Prob. 62ECh. 8.4 - Prob. 63ECh. 8.4 - Prob. 64ECh. 8.4 - Prob. 65ECh. 8.4 - Arc length Show that the arc length of the graph...Ch. 8.4 - Area of a Lune The crescent shaped region bounded...Ch. 8.4 - Prob. 68ECh. 8.4 - Prob. 69ECh. 8.5 - Partial Fraction Decomposition In Exercises 1-4,...Ch. 8.5 - Guidelines for Solving the Basic Equation In your...Ch. 8.5 - Prob. 3ECh. 8.5 - Prob. 4ECh. 8.5 - Prob. 5ECh. 8.5 - Prob. 6ECh. 8.5 - Prob. 7ECh. 8.5 - Prob. 8ECh. 8.5 - Prob. 9ECh. 8.5 - Prob. 10ECh. 8.5 - Using Partial Fractions In Exercises 3-20, use...Ch. 8.5 - Prob. 12ECh. 8.5 - Prob. 13ECh. 8.5 - Prob. 14ECh. 8.5 - Prob. 15ECh. 8.5 - Using Partial Fractions In Exercises 3-20, use...Ch. 8.5 - Prob. 17ECh. 8.5 - Prob. 18ECh. 8.5 - Prob. 19ECh. 8.5 - Prob. 20ECh. 8.5 - Prob. 21ECh. 8.5 - Prob. 22ECh. 8.5 - Prob. 23ECh. 8.5 - Prob. 24ECh. 8.5 - Prob. 25ECh. 8.5 - Prob. 26ECh. 8.5 - Prob. 27ECh. 8.5 - Prob. 28ECh. 8.5 - Prob. 29ECh. 8.5 - Finding an Indefinite Integral In Exercises 25-32,...Ch. 8.5 - Prob. 31ECh. 8.5 - Prob. 32ECh. 8.5 - Prob. 33ECh. 8.5 - Prob. 34ECh. 8.5 - Prob. 35ECh. 8.5 - Prob. 36ECh. 8.5 - Prob. 37ECh. 8.5 - Prob. 38ECh. 8.5 - Prob. 39ECh. 8.5 - Prob. 40ECh. 8.5 - Prob. 41ECh. 8.5 - Prob. 42ECh. 8.5 - Prob. 43ECh. 8.5 - Area In Exercises 41-44, use partial fractions to...Ch. 8.5 - Prob. 45ECh. 8.5 - Prob. 46ECh. 8.5 - Prob. 47ECh. 8.5 - Volume Consider the region bounded by the graph of...Ch. 8.5 - Epidemic Model A single infected individual enters...Ch. 8.5 - Chemical Reaction In a chemical reaction, one unit...Ch. 8.5 - Prob. 51ECh. 8.5 - Prove 227=01x4(1x)41+x2dxCh. 8.5 - Prob. 53ECh. 8.6 - Prob. 1ECh. 8.6 - Prob. 2ECh. 8.6 - Using the Trapezoidal Rule and Simpson's Rule In...Ch. 8.6 - Prob. 4ECh. 8.6 - Prob. 5ECh. 8.6 - Prob. 6ECh. 8.6 - Prob. 7ECh. 8.6 - Prob. 8ECh. 8.6 - Using the Trapezoidal Rule and Simpson's Rule In...Ch. 8.6 - Using the Trapezoidal Rule and Simpson's Rule In...Ch. 8.6 - Prob. 11ECh. 8.6 - Prob. 12ECh. 8.6 - Prob. 13ECh. 8.6 - Prob. 14ECh. 8.6 - Using the Trapezoidal Rule and Simpsonss Rule In...Ch. 8.6 - Prob. 16ECh. 8.6 - Prob. 17ECh. 8.6 - Using the Trapezoidal Rule and Simpsonss Rule In...Ch. 8.6 - Prob. 19ECh. 8.6 - Prob. 20ECh. 8.6 - Using the Trapezoidal Rule and Simpsonss Rule In...Ch. 8.6 - Prob. 22ECh. 8.6 - Prob. 23ECh. 8.6 - Prob. 24ECh. 8.6 - Prob. 25ECh. 8.6 - Estimating Errors In Exercises 25-28, use the...Ch. 8.6 - Prob. 27ECh. 8.6 - Estimating Errors In Exercises 25-28, use the...Ch. 8.6 - Estimating Errors In Exercises 29-32, use the...Ch. 8.6 - Prob. 30ECh. 8.6 - Prob. 31ECh. 8.6 - Prob. 32ECh. 8.6 - Prob. 33ECh. 8.6 - Prob. 34ECh. 8.6 - Finding the Area of a Region Approximate the area...Ch. 8.6 - Prob. 36ECh. 8.6 - Prob. 37ECh. 8.6 - HOW DO YOU SEE IT? The function f is concave...Ch. 8.6 - Prob. 39ECh. 8.6 - Prob. 40ECh. 8.6 - Prob. 41ECh. 8.6 - Prob. 42ECh. 8.6 - Prob. 43ECh. 8.6 - Approximating a Function The table lists several...Ch. 8.6 - Prob. 46ECh. 8.6 - Prob. 47ECh. 8.7 - CONCEPT CHECK Integration by Tables Which formula...Ch. 8.7 - Prob. 2ECh. 8.7 - Integration by Tables In Exercises 3 and 4 use a...Ch. 8.7 - Prob. 4ECh. 8.7 - Prob. 5ECh. 8.7 - Prob. 6ECh. 8.7 - Prob. 7ECh. 8.7 - Prob. 8ECh. 8.7 - Prob. 9ECh. 8.7 - Prob. 10ECh. 8.7 - Prob. 11ECh. 8.7 - Prob. 12ECh. 8.7 - Prob. 13ECh. 8.7 - Prob. 14ECh. 8.7 - Prob. 15ECh. 8.7 - Prob. 16ECh. 8.7 - Prob. 17ECh. 8.7 - Prob. 18ECh. 8.7 - Finding an Indefinite Integral In Exercises 19-40,...Ch. 8.7 - Finding an Indefinite Integral In Exercises 19-40,...Ch. 8.7 - Prob. 21ECh. 8.7 - Prob. 22ECh. 8.7 - Finding an Indefinite Integral In Exercises 19-40,...Ch. 8.7 - Prob. 24ECh. 8.7 - Prob. 25ECh. 8.7 - Prob. 26ECh. 8.7 - Finding an Indefinite Integral In Exercises 19-40,...Ch. 8.7 - Prob. 28ECh. 8.7 - Prob. 29ECh. 8.7 - Prob. 30ECh. 8.7 - Prob. 31ECh. 8.7 - Prob. 32ECh. 8.7 - Prob. 33ECh. 8.7 - Prob. 34ECh. 8.7 - Finding an Indefinite Integral In Exercises 1940,...Ch. 8.7 - Prob. 36ECh. 8.7 - Prob. 37ECh. 8.7 - Prob. 38ECh. 8.7 - Prob. 39ECh. 8.7 - Prob. 40ECh. 8.7 - Prob. 41ECh. 8.7 - Prob. 42ECh. 8.7 - Prob. 43ECh. 8.7 - Prob. 44ECh. 8.7 - Evaluating a Definite Integral In Exercises 4148,...Ch. 8.7 - Prob. 46ECh. 8.7 - Prob. 47ECh. 8.7 - Prob. 48ECh. 8.7 - Prob. 49ECh. 8.7 - Prob. 50ECh. 8.7 - Prob. 51ECh. 8.7 - Prob. 52ECh. 8.7 - Prob. 53ECh. 8.7 - Verifying a Formula In Exercises 49-54, verify the...Ch. 8.7 - Prob. 55ECh. 8.7 - Prob. 56ECh. 8.7 - Prob. 57ECh. 8.7 - Prob. 58ECh. 8.7 - Prob. 59ECh. 8.7 - Prob. 60ECh. 8.7 - Prob. 61ECh. 8.7 - Prob. 62ECh. 8.7 - Prob. 63ECh. 8.7 - Prob. 64ECh. 8.7 - EXPLORING CONCEPTS Finding a Pattern (a) Find...Ch. 8.7 - Prob. 66ECh. 8.7 - Prob. 67ECh. 8.7 - Prob. 68ECh. 8.7 - Prob. 69ECh. 8.7 - Prob. 70ECh. 8.7 - Prob. 71ECh. 8.7 - Building Design The cross section of a precast...Ch. 8.7 - Prob. 73ECh. 8.8 - CONCEPT CHECK Improper Integrals Describe two ways...Ch. 8.8 - Prob. 2ECh. 8.8 - Prob. 3ECh. 8.8 - Prob. 4ECh. 8.8 - Determining Whether an Integral Is Improper In...Ch. 8.8 - Prob. 6ECh. 8.8 - Prob. 7ECh. 8.8 - Determining Whether an Integral Is Improper In...Ch. 8.8 - Prob. 9ECh. 8.8 - Prob. 10ECh. 8.8 - Determining Whether an Integral Is Improper In...Ch. 8.8 - Prob. 12ECh. 8.8 - Prob. 13ECh. 8.8 - Evaluating an Improper Integral In Exercises...Ch. 8.8 - Evaluating an Improper Integral In Exercises...Ch. 8.8 - Prob. 16ECh. 8.8 - Prob. 17ECh. 8.8 - Prob. 18ECh. 8.8 - Prob. 19ECh. 8.8 - Prob. 20ECh. 8.8 - Prob. 21ECh. 8.8 - Prob. 22ECh. 8.8 - Evaluating an Improper Integral In Exercises 1732,...Ch. 8.8 - Prob. 24ECh. 8.8 - Evaluating an Improper Integral In Exercises 1732,...Ch. 8.8 - Evaluating an Improper Integral In Exercises 1732,...Ch. 8.8 - Prob. 27ECh. 8.8 - Prob. 28ECh. 8.8 - Prob. 29ECh. 8.8 - Prob. 30ECh. 8.8 - Prob. 31ECh. 8.8 - Prob. 32ECh. 8.8 - Prob. 33ECh. 8.8 - Prob. 34ECh. 8.8 - Prob. 35ECh. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Prob. 40ECh. 8.8 - Prob. 41ECh. 8.8 - Prob. 42ECh. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Prob. 46ECh. 8.8 - Evaluating an Improper Integral In Exercises 3348,...Ch. 8.8 - Prob. 48ECh. 8.8 - Finding Values In Exercises 49 and 50, determine...Ch. 8.8 - Prob. 50ECh. 8.8 - Prob. 51ECh. 8.8 - Prob. 52ECh. 8.8 - Prob. 53ECh. 8.8 - Convergence or Divergence In Exercises 5360, use...Ch. 8.8 - Prob. 55ECh. 8.8 - Convergence or Divergence In Exercises 5360, use...Ch. 8.8 - Prob. 57ECh. 8.8 - Prob. 58ECh. 8.8 - Convergence or Divergence In Exercises 5360, use...Ch. 8.8 - Prob. 60ECh. 8.8 - Prob. 61ECh. 8.8 - Prob. 62ECh. 8.8 - Prob. 63ECh. 8.8 - Prob. 64ECh. 8.8 - Area In Exercises 63-66, find the area of the...Ch. 8.8 - Area In Exercises 63-66, find the area of the...Ch. 8.8 - Area and Volume In Exercises 67 and 68, consider...Ch. 8.8 - Prob. 68ECh. 8.8 - Prob. 69ECh. 8.8 - Prob. 70ECh. 8.8 - Propulsion In Exercises 71 and 72, use the weight...Ch. 8.8 - Prob. 72ECh. 8.8 - Prob. 73ECh. 8.8 - Prob. 74ECh. 8.8 - Normal Probability The mean height of American men...Ch. 8.8 - Prob. 76ECh. 8.8 - Prob. 77ECh. 8.8 - Prob. 78ECh. 8.8 - Prob. 79ECh. 8.8 - Prob. 80ECh. 8.8 - Prob. 81ECh. 8.8 - Prob. 82ECh. 8.8 - Prob. 83ECh. 8.8 - Prob. 84ECh. 8.8 - Prob. 85ECh. 8.8 - Prob. 86ECh. 8.8 - Prob. 87ECh. 8.8 - Prob. 88ECh. 8.8 - Prob. 89ECh. 8.8 - Prob. 90ECh. 8.8 - Prob. 91ECh. 8.8 - Prob. 92ECh. 8.8 - Prob. 93ECh. 8.8 - Prob. 94ECh. 8.8 - Prob. 95ECh. 8.8 - Prob. 96ECh. 8.8 - Prob. 97ECh. 8.8 - Prob. 98ECh. 8.8 - Prob. 99ECh. 8.8 - Prob. 100ECh. 8.8 - Prob. 101ECh. 8.8 - Prob. 102ECh. 8.8 - Prob. 103ECh. 8.8 - Prob. 104ECh. 8.8 - u -Substitution In Exercises 105 and 106, rewrite...Ch. 8.8 - Prob. 106ECh. 8.8 - Prob. 107ECh. 8 - Using Basic Integration Rules In Exercises 18, use...Ch. 8 - Using Basic Integration Rules In Exercises 18, use...Ch. 8 - Prob. 3RECh. 8 - Prob. 4RECh. 8 - Using Basic Integration Rules In Exercises 18, use...Ch. 8 - Prob. 6RECh. 8 - Prob. 7RECh. 8 - Prob. 8RECh. 8 - Prob. 9RECh. 8 - Prob. 10RECh. 8 - Prob. 11RECh. 8 - Prob. 12RECh. 8 - Prob. 13RECh. 8 - Prob. 14RECh. 8 - Prob. 15RECh. 8 - Prob. 16RECh. 8 - Prob. 17RECh. 8 - Prob. 18RECh. 8 - Prob. 19RECh. 8 - Prob. 20RECh. 8 - Prob. 21RECh. 8 - Prob. 22RECh. 8 - Prob. 23RECh. 8 - Prob. 24RECh. 8 - Prob. 25RECh. 8 - Prob. 26RECh. 8 - Prob. 27RECh. 8 - Prob. 28RECh. 8 - Prob. 29RECh. 8 - Prob. 30RECh. 8 - Prob. 31RECh. 8 - Prob. 32RECh. 8 - Prob. 33RECh. 8 - Prob. 34RECh. 8 - Prob. 35RECh. 8 - Prob. 36RECh. 8 - Prob. 37RECh. 8 - Prob. 38RECh. 8 - Using Partial Fractions In Exercises 3744, use...Ch. 8 - Prob. 40RECh. 8 - Prob. 41RECh. 8 - Prob. 42RECh. 8 - Prob. 43RECh. 8 - Prob. 44RECh. 8 - Prob. 45RECh. 8 - Prob. 46RECh. 8 - Prob. 47RECh. 8 - Prob. 48RECh. 8 - Prob. 49RECh. 8 - Prob. 50RECh. 8 - Prob. 51RECh. 8 - Prob. 52RECh. 8 - Prob. 53RECh. 8 - Prob. 54RECh. 8 - Prob. 55RECh. 8 - Prob. 56RECh. 8 - Prob. 57RECh. 8 - Prob. 58RECh. 8 - Prob. 59RECh. 8 - Prob. 60RECh. 8 - Prob. 61RECh. 8 - Prob. 62RECh. 8 - Prob. 63RECh. 8 - Prob. 64RECh. 8 - Prob. 65RECh. 8 - Prob. 66RECh. 8 - Prob. 67RECh. 8 - Prob. 68RECh. 8 - Prob. 69RECh. 8 - Prob. 70RECh. 8 - Prob. 71RECh. 8 - Prob. 72RECh. 8 - Prob. 73RECh. 8 - Prob. 74RECh. 8 - Prob. 75RECh. 8 - Prob. 76RECh. 8 - Prob. 77RECh. 8 - Prob. 78RECh. 8 - Prob. 79RECh. 8 - Prob. 80RECh. 8 - Prob. 81RECh. 8 - Prob. 82RECh. 8 - Prob. 83RECh. 8 - Prob. 84RECh. 8 - Prob. 85RECh. 8 - Prob. 86RECh. 8 - Present Value The board of directors of a...Ch. 8 - Prob. 88RECh. 8 - Prob. 89RECh. 8 - Prob. 1PSCh. 8 - Prob. 2PSCh. 8 - Prob. 3PSCh. 8 - Prob. 4PSCh. 8 - Area Use the substitution u=tanx2 v to find the...Ch. 8 - Prob. 6PSCh. 8 - Prob. 7PSCh. 8 - Prob. 8PSCh. 8 - Prob. 9PSCh. 8 - Prob. 10PSCh. 8 - Prob. 11PSCh. 8 - Prob. 12PSCh. 8 - Prob. 13PSCh. 8 - Prob. 14PSCh. 8 - Prob. 15PSCh. 8 - Prob. 16PSCh. 8 - Prob. 17PSCh. 8 - Prob. 18PSCh. 8 - Prob. 19PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Computer giving into girl. Show the algebra necessary to convert the integral into a form where you may use one of your integration formulas.arrow_forwardUsing Completing the square evaluate the integral belowarrow_forwarda. Approximate the value of the integral by using rectangles. For your approximation use right endpoints and let n = 4 b. Evaluate the integral by interpreting it in terms of areas. Draw a picture c. Evaluate the integral using the Fundamental Theorem of Calculus Part 2 FTC2)arrow_forward
- General construction of Riemann integral of function f in ℝ³arrow_forwardUsing the Fundamental Theorem of Calculus, evaluate the integral.arrow_forwardEvaluate the integral. Also, discuss or explain the step by step process with the correct mathematical principle behind each step in obtaining the answer.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Evaluating Indefinite Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=-xHA2RjVkwY;License: Standard YouTube License, CC-BY
Calculus - Lesson 16 | Indefinite and Definite Integrals | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=bMnMzNKL9Ks;License: Standard YouTube License, CC-BY