Chapter 9, Problem 9.20P

(a)

To determine

Describe puck’s coordinates x and y using Newton’s second law.

Answer to Problem 9.20P

Using Newton’s second law, the puck’s coordinates are $\underset{\_}{\ddot{x}={\Omega }^{2}x+2\Omega \dot{y}}$ and $\underset{\_}{\ddot{y}={\Omega }^{2}y+2\Omega \dot{x}}$.

Explanation of Solution

Write the expression for the centrifugal force on puck,

    $F_{cf}=m\left(\Omega \times r\right)\times \Omega$        (I)

Here, $F_{cf}$ is the centrifugal force on puck, $\Omega$ is the angular velocity of the turntable, $m$ is mass and $r$ is the position vector.

Write the expression for the Coriolis force on puck,

    $F_c=2m\dot{r}\times \Omega$        (II)

Here, $F_c$ is the Coriolis force on puck and $\dot{r}$ is the linear velocity.

Write the expression for the net force act on the puck,

    $F=F_{cf}+F_c$        (III)

Here, $F$ is the net force act on the puck.

Substitute (I) and (II) in (III),

    $F=m\left(\Omega \times r\right)\times \Omega +2m\dot{r}\times \Omega$        (IV)

Let us consider the turntable is along $xy$ plane and angular velocity along $z$ -direction.

Write the expression for the position vector,

    $r=xi+yj$        (V)

Write the expression for the angular velocity,

    $\Omega =\Omega k$        (VI)

(V) X (VI),

    $\begin{array}{c}\Omega \times r=\left|\begin{array}{ccc}i& j& k\\ 0& 0& \Omega \\ x& y& 0\end{array}\right|\\ =i\left(0-\Omega y\right)-j\left(0-\Omega x\right)+k\left(0-0\right)\\ =-\Omega yi+\Omega xj\end{array}$        (VII)

(VII) X (VI),

    $\begin{array}{c}\left(\Omega \times r\right)\times \Omega =\left|\begin{array}{ccc}i& j& k\\ -\Omega y& \Omega x& 0\\ 0& 0& \Omega \end{array}\right|\\ =i\left({\Omega }^{2}x-0\right)-j\left(-{\Omega }^{2}y-0\right)+k\left(0-0\right)\\ ={\Omega }^{2}xi+{\Omega }^{2}yj\end{array}$        (VIII)

Write the expression for the linear velocity,

    $\dot{r}=\dot{x}i+\dot{y}j$        (IX)

(IX) X (VI),

    $\begin{array}{c}\dot{r}\times \Omega =\left|\begin{array}{ccc}i& j& k\\ \dot{x}& \dot{y}& 0\\ 0& 0& \Omega \end{array}\right|\\ =i\left(\Omega \dot{y}-0\right)-j\left(\Omega \dot{x}-0\right)+k\left(0-0\right)\\ =\Omega \dot{y}i-\Omega \dot{x}j\end{array}$        (X)

Substitute  $m\ddot{r}$ for $F$, ${\Omega }^{2}xi+{\Omega }^{2}yj$ for $\left(\Omega \times r\right)\times \Omega$ and $\Omega \dot{y}i-\Omega \dot{x}j$ for $\dot{r}\times \Omega$ in (IV),

    $\begin{array}{c}m\ddot{r}=m\left({\Omega }^{2}xi+{\Omega }^{2}yj\right)+2m\left(\Omega \dot{y}i-\Omega \dot{x}j\right)\\ \ddot{r}=\left({\Omega }^{2}xi+{\Omega }^{2}yj\right)+2\left(\Omega \dot{y}i-\Omega \dot{x}j\right)\\ =\left({\Omega }^{2}x+2\Omega \dot{y}\right)i+\left({\Omega }^{2}y-2\Omega \dot{x}\right)j\end{array}$        (XI)

Compare the above equation with (IX), and we get the equation for $\ddot{x}$ and $\ddot{y}$,

    $\ddot{x}={\Omega }^{2}x+2\Omega \dot{y}$        (XII)

    $\ddot{y}={\Omega }^{2}y+2\Omega \dot{x}$        (XIII)

Therefore, using Newton’s second law, the puck’s coordinates are $\underset{\_}{\ddot{x}={\Omega }^{2}x+2\Omega \dot{y}}$ and $\underset{\_}{\ddot{y}={\Omega }^{2}y+2\Omega \dot{x}}$.

(b)

To determine

The general solution for the equation $\eta =x+iy$.

Answer to Problem 9.20P

The general solution for the equation $\eta =x+iy$ is $\underset{\_}{\eta \left(t\right)=e^{-i\Omega t}\left(C_1+C_{2}t\right)}$.

Explanation of Solution

Write the given tricky expression,

    $\eta =x+iy$        (XIV)

Differentiate (XIV),

    $\dot{\eta }=\dot{x}+i\dot{y}$        (XV)

Again differentiate,

    $\ddot{\eta }=\ddot{x}+i\ddot{y}$        (XVI)

Substitute ${\Omega }^{2}x+2\Omega \dot{y}$ for $\ddot{x}$ and ${\Omega }^{2}y-2\Omega \dot{x}$ for $\ddot{y}$ in (XVI),

    $\begin{array}{c}\ddot{\eta }=\left({\Omega }^{2}x+2\Omega \dot{y}\right)+i\left({\Omega }^{2}y-2\Omega \dot{x}\right)\\ =\left({\Omega }^{2}x+i{\Omega }^{2}y\right)+2\left(\Omega \dot{y}-i\Omega \dot{x}\right)\\ ={\Omega }^2\left(x+iy\right)+2\Omega \left(\dot{y}-i\dot{x}\right)\\ ={\Omega }^2\left(x+iy\right)+2\Omega \frac{i}{i}\left(\dot{y}-i\dot{x}\right)\end{array}$        (XVII)

    $\begin{array}{c}\eta ={\Omega }^2\left(x+iy\right)+2\Omega i\left(\frac{\dot{y}}{i}-\dot{x}\right)\\ ={\Omega }^2\left(x+iy\right)+2\Omega i\left(\left(\frac{i}{i}\right)\left(\frac{\dot{y}}{i}\right)-\dot{x}\right)\\ ={\Omega }^2\left(x+iy\right)+2\Omega i\left(\left(\frac{i\dot{y}}{i^2}\right)-\dot{x}\right)\\ ={\Omega }^2\left(x+iy\right)+2\Omega i\left(\frac{i\dot{y}}{\left(-1\right)}-\dot{x}\right)\end{array}$

    $\begin{array}{c}\eta ={\Omega }^2\left(x+iy\right)+2\Omega i\left(-i\dot{y}-\dot{x}\right)\\ ={\Omega }^2\left(x+iy\right)-2\Omega i\left(\dot{x}+i\dot{y}\right)\end{array}$

Substitute $\eta$ for $x+iy$ and $\dot{\eta }$ for $\dot{x}+i\dot{y}$ .in (XVII),

    $\ddot{\eta }={\Omega }^2\eta -2\Omega i\dot{\eta }$        (XVIII)

Consider the above equation in the form of $\eta =e^{-i\Omega t}$, so the above equation,

    $\begin{array}{c}\frac{d^2}{d{t}^2}\left(e^{-i\Omega t}\right)={\Omega }^2{e}^{-i\Omega t}-2\Omega i\frac{d}{dt}\left(e^{-i\Omega t}\right)\\ i^2{\alpha }^2{e}^{-i\Omega t}={\Omega }^2{e}^{-i\Omega t}+2\Omega i^2\alpha \left(e^{-i\Omega t}\right)\\ i^2{\alpha }^2={\Omega }^2+2\Omega i^2\alpha \\ -{\alpha }^2={\Omega }^2-2\Omega \alpha \end{array}$

Rewrite the equation,

    $\begin{array}{c}{\Omega }^2-2\Omega \alpha +{\alpha }^2=0\\ {\left(\alpha -\Omega \right)}^2=0\\ \alpha =\Omega ,\Omega \end{array}$

The general solution for this equation,

    $\eta \left(t\right)=e^{-i\Omega t}\left(C_1+C_{2}t\right)$        (XIX)

Here, $C_1$ and $C_2$ are the constants and these constants does not depend on time.

Therefore, the general solution for the equation $\eta =x+iy$ is $\underset{\_}{\eta \left(t\right)=e^{-i\Omega t}\left(C_1+C_{2}t\right)}$.

(c)

To determine

Show that the given equations.

Answer to Problem 9.20P

The given equations are proved here.

Explanation of Solution

From part (b),

    $\eta \left(t\right)=e^{-i\Omega t}\left(C_1+C_{2}t\right)$        (XX)

    $\begin{array}{l}\eta \left(0\right)=e^{-i\Omega \left(0\right)}\left(C_1+C_2\left(0\right)\right)\\ \eta \left(0\right)=C_1\end{array}$

Substitute $x_0+i{y}_0$ for $\eta \left(0\right)$ in the above equation,

    $\begin{array}{c}{C}_1=x_0+i{y}_0\\ =x_0+i{v}_{y_0}t\end{array}$

Since this constant does not depends on time.

So substitute $0$ for $t$ in the above equation,

    $\begin{array}{c}{C}_1=x_0+i{v}_{y_0}\left(0\right)\\ =x_0\end{array}$

Differentiate the equation (XX) with respect to $t$,

    $\begin{array}{c}\dot{\eta }\left(t\right)=-i\Omega e^{-i\Omega t}\left(C_1+C_{2}t\right)+e^{-i\Omega t}\left(0+C_2\right)\\ =e^{-i\Omega t}\left(C_2-i\Omega \left(C_1+C_{2}t\right)\right)\end{array}$

Substitute $0$ for $t$ in the above equation,

    $\begin{array}{c}\dot{\eta }\left(0\right)=e^{-i\Omega \left(0\right)}\left(C_2-i\Omega \left(C_1+C_2\left(0\right)\right)\right)\\ =C_2-i\Omega C_1\end{array}$

Substitute ${\dot{x}}_0+i{\dot{y}}_0$ for $\dot{\eta }\left(0\right)$ and $x_0$ for $C_1$ in the above equation,

    ${\dot{x}}_0+i{\dot{y}}_0=C_2-i\Omega \left(x_0\right)$

Rewrite the above equation for $C_2$ ,

    $C_2={\dot{x}}_0+i{\dot{y}}_0+i\Omega \left(x_0\right)$

Substitute $v_{x0}$ for ${\dot{x}}_0$ and $v_{y0}$ for ${\dot{y}}_0$ in the above equation,

    $\begin{array}{c}{C}_2=v_{x0}+i{v}_{y0}+i\Omega \left(x_0\right)\\ =v_{x0}+i{v}_{y0}+i\Omega x_0\end{array}$

Substitute $x_0$ for $C_1$ and $v_{x0}+i{v}_{y0}+i\Omega x_0$ for $C_2$ in (XX),

    $\begin{array}{c}\eta \left(t\right)=e^{-\Omega t}\left(x_0+\left(v_{x0}+i{v}_{y0}+i\Omega x_0\right)t\right)\\ =e^{-\Omega t}\left(x_0+v_{x0}t\right)+i{e}^{-\Omega t}\left(v_{y0}+\Omega x_0\right)t\\ =\left[\begin{array}{l}\left(x_0+v_{x0}t\right)\cos \Omega t-i\left(x_0+v_{x0}t\right)\sin \Omega t+\\ i\left(v_{y0}+\Omega x_0\right)t\cos \Omega t-t^2\left(v_{y0}+\Omega x_0\right)\sin \Omega t\end{array}\right]\\ =\left[\begin{array}{l}\left(x_0+v_{x0}t\right)\cos \Omega t+\left(v_{y0}+\Omega x_0\right)\sin \Omega t\\ +i\left\{-\left(x_0+v_{x0}t\right)\sin \Omega t+\left(v_{y0}+\Omega x_0\right)t\cos \Omega t\right\}\end{array}\right]\end{array}$

From the above equation, write the real part and imaginary part separately.

    $\begin{array}{c}x\left(t\right)=\left(x_0+v_{y0}t\right)\cos \Omega t+\left(v_{y0}+\Omega x_0\right)t\sin \Omega t\\ y\left(t\right)=-\left(x_0+v_{y0}t\right)\sin \Omega t+\left(v_{y0}+\Omega x_0\right)t\cos \Omega t\end{array}$        (XXI)

Therefore, the given equations are proved here.

(d)

To determine

Draw and describe the behavior of the puck when it has large $t$.

Answer to Problem 9.20P

The behavior of the puck when it has large $t$ is drawn and described here.

Explanation of Solution

Write the expression of motion for the coordinates x and y,

    $\begin{array}{l}x\left(t\right)=t\left(B_1\cos \Omega t+B_2\sin \Omega t\right)\\ y\left(t\right)=t\left(-B_1\sin \Omega t+B_2\cos \Omega t\right)\end{array}$        (XXII)

Here, $B_1$ and $B_2$ are functions.

Let us write the functions,

    $A=\sqrt{B_1^2+B_2^2}$

Here, $B_1=v_{x0}$ and $B_2=v_{y0}+\Omega x_0$ .

Therefore, the equation (XXII) becomes,

    $\begin{array}{l}x\left(t\right)=tA\cos \left(\Omega t-\delta \right)\\ y\left(t\right)=-tA\sin \left(\Omega t-\delta \right)\end{array}$        (XXIII)

In this case, the path of the puck should be spherical shape, because that circle is continuously growing at constant rate.

It is moving like a circle in a clockwise direction. The factor t explains that the circle grows at a constant rate. In this situation, the puck moves in a spiral orbit.

The figure 1 is the behavior of the puck.

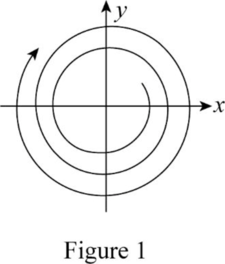
Therefore, the behavior of the puck when it has large $t$ is drawn and described here.