
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter A.4, Problem 38E
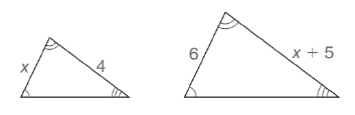
Determine the length
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter A Solutions
Elementary Geometry For College Students, 7e
Ch. A.1 - Which axiom of equality is illustrated in each of...Ch. A.1 - Prob. 2ECh. A.1 - Prob. 3ECh. A.1 - Prob. 4ECh. A.1 - Prob. 5ECh. A.1 - Prob. 6ECh. A.1 - Prob. 7ECh. A.1 - Prob. 8ECh. A.1 - Prob. 9ECh. A.1 - Prob. 10E
Ch. A.1 - Prob. 11ECh. A.1 - Prob. 12ECh. A.1 - The four owners of a shop realize a loss of 240 in...Ch. A.1 - Bill works at a weekend convention by selling...Ch. A.1 - Use the Distributive Axiom to simplify each...Ch. A.1 - Use the Distributive Axiom to simplify each...Ch. A.1 - Simplify each expression: a 6+4 c 16x2y9x2y b...Ch. A.1 - Prob. 18ECh. A.1 - Prob. 19ECh. A.1 - Prob. 20ECh. A.1 - Prob. 21ECh. A.1 - Prob. 22ECh. A.1 - Prob. 23ECh. A.1 - Prob. 24ECh. A.1 - Prob. 25ECh. A.1 - Prob. 26ECh. A.1 - Prob. 27ECh. A.1 - Prob. 28ECh. A.1 - Prob. 29ECh. A.1 - Prob. 30ECh. A.2 - In Exercises 1 to 6, simplify by combining similar...Ch. A.2 - Prob. 2ECh. A.2 - Prob. 3ECh. A.2 - Prob. 4ECh. A.2 - Prob. 5ECh. A.2 - Prob. 6ECh. A.2 - Prob. 7ECh. A.2 - Prob. 8ECh. A.2 - Prob. 9ECh. A.2 - Prob. 10ECh. A.2 - Prob. 11ECh. A.2 - Prob. 12ECh. A.2 - Prob. 13ECh. A.2 - Prob. 14ECh. A.2 - Prob. 15ECh. A.2 - Prob. 16ECh. A.2 - Prob. 17ECh. A.2 - Prob. 18ECh. A.2 - Prob. 19ECh. A.2 - Prob. 20ECh. A.2 - Prob. 21ECh. A.2 - Prob. 22ECh. A.2 - Prob. 23ECh. A.2 - Prob. 24ECh. A.2 - Prob. 25ECh. A.2 - Prob. 26ECh. A.2 - Prob. 27ECh. A.2 - Prob. 28ECh. A.2 - Prob. 29ECh. A.2 - Prob. 30ECh. A.2 - Prob. 31ECh. A.2 - Prob. 32ECh. A.2 - Prob. 33ECh. A.2 - Prob. 34ECh. A.2 - Prob. 35ECh. A.2 - Prob. 36ECh. A.3 - If line segment AB and line segment CD in the...Ch. A.3 - Prob. 2ECh. A.3 - Prob. 3ECh. A.3 - Prob. 4ECh. A.3 - Prob. 5ECh. A.3 - Prob. 6ECh. A.3 - Prob. 7ECh. A.3 - Prob. 8ECh. A.3 - Prob. 9ECh. A.3 - Of several angles, the degree measures are related...Ch. A.3 - Prob. 11ECh. A.3 - Prob. 12ECh. A.3 - Prob. 13ECh. A.3 - Prob. 14ECh. A.3 - Prob. 15ECh. A.3 - Prob. 16ECh. A.3 - Prob. 17ECh. A.3 - Prob. 18ECh. A.3 - Prob. 19ECh. A.3 - Prob. 20ECh. A.3 - Prob. 21ECh. A.3 - Prob. 22ECh. A.3 - Prob. 23ECh. A.3 - Prob. 24ECh. A.3 - Prob. 25ECh. A.3 - Prob. 26ECh. A.3 - Prob. 27ECh. A.3 - Prob. 28ECh. A.3 - Prob. 29ECh. A.3 - Prob. 30ECh. A.3 - Prob. 31ECh. A.3 - Prob. 32ECh. A.4 - Prob. 1ECh. A.4 - Note: Exercises preceded by an asterisk are of a...Ch. A.4 - Prob. 3ECh. A.4 - Prob. 4ECh. A.4 - Prob. 5ECh. A.4 - Prob. 6ECh. A.4 - In Exercises 5 to 8, factor each difference of two...Ch. A.4 - In Exercises 5 to 8, factor each difference of two...Ch. A.4 - Prob. 9ECh. A.4 - Prob. 10ECh. A.4 - In Exercises 9 to 16, factor each trinomial...Ch. A.4 - Prob. 12ECh. A.4 - Prob. 13ECh. A.4 - Prob. 14ECh. A.4 - Prob. 15ECh. A.4 - Prob. 16ECh. A.4 - Prob. 17ECh. A.4 - Prob. 18ECh. A.4 - Prob. 19ECh. A.4 - Prob. 20ECh. A.4 - Prob. 21ECh. A.4 - Prob. 22ECh. A.4 - Prob. 23ECh. A.4 - Prob. 24ECh. A.4 - Prob. 25ECh. A.4 - Prob. 26ECh. A.4 - Prob. 27ECh. A.4 - Prob. 28ECh. A.4 - In Exercises 25 to 32, solve each quadratic...Ch. A.4 - In Exercises 25 to 32, solve each quadratic...Ch. A.4 - Prob. 31ECh. A.4 - Prob. 32ECh. A.4 - Prob. 33ECh. A.4 - Prob. 34ECh. A.4 - Prob. 35ECh. A.4 - Prob. 36ECh. A.4 - Given that the area of the rectangle shown is 66,...Ch. A.4 - Determine the length x by solving either the...Ch. A.4 - Find the length a by solving the equation...Ch. A.4 - Prob. 40ECh. A.4 - Prob. 41ECh. A.5 - Use your calculator to find the approximate value...Ch. A.5 - Prob. 2ECh. A.5 - Prob. 3ECh. A.5 - Prob. 4ECh. A.5 - Prob. 5ECh. A.5 - Prob. 6ECh. A.5 - Prob. 7ECh. A.5 - Prob. 8ECh. A.5 - Use your calculator to verify that the following...Ch. A.5 - Prob. 10ECh. A.5 - Prob. 11ECh. A.5 - Prob. 12ECh. A.5 - Prob. 13ECh. A.5 - Prob. 14ECh. A.5 - Prob. 15ECh. A.5 - Prob. 16ECh. A.5 - Prob. 17ECh. A.5 - Prob. 18ECh. A.5 - Prob. 19ECh. A.5 - Prob. 20ECh. A.5 - Prob. 21ECh. A.5 - Prob. 22ECh. A.5 - Prob. 23ECh. A.5 - Prob. 24ECh. A.5 - Prob. 25ECh. A.5 - Prob. 26ECh. A.5 - Prob. 27ECh. A.5 - Prob. 28ECh. A.5 - Prob. 29ECh. A.5 - Prob. 30ECh. A.5 - Prob. 31ECh. A.5 - Prob. 32ECh. A.5 - Prob. 33ECh. A.5 - Prob. 34ECh. A.5 - Prob. 35ECh. A.5 - Prob. 36ECh. A.5 - Prob. 37ECh. A.5 - Prob. 38ECh. A.5 - Prob. 39E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Intermediate AlgebraAlgebraISBN:9781285195728Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning


Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Intermediate Algebra
Algebra
ISBN:9781285195728
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
What is a Linear Equation in One Variable?; Author: Don't Memorise;https://www.youtube.com/watch?v=lDOYdBgtnjY;License: Standard YouTube License, CC-BY
Linear Equation | Solving Linear Equations | What is Linear Equation in one variable ?; Author: Najam Academy;https://www.youtube.com/watch?v=tHm3X_Ta_iE;License: Standard YouTube License, CC-BY