
Concept explainers
For the component described in the problem indicated,determine (a) the principal mass moments of inertia at the origin (b) the principal axes of inertia at the origin. Sketch the body and show the orientation of the principal axes of inertia relative to the x, y, and z axes.
Probs. B.35 and B.39
(a)
The principal mass moment of inertias at the origin.
Answer to Problem B.71P
The principal mass moment of inertias at the origin are
Explanation of Solution
Given information:
The density of the steel is
The following figure represents the given system.
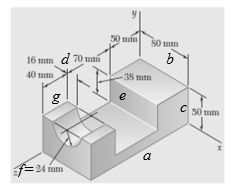
Figure-(1)
Concept used:
Write the expression for the mass of component 1.
Here, the mass of component 1 is
Write the expression for the volume of the component 1.
Here, the sides of the component is
Write the expression for the mass moment of inertia for component 1.
Here, the mass moment of inertia for component 1 is
Write the expression for the mass moment of inertia with respect to centroidal axis.
Write the expression for the centroidal axis from the reference axis.
Write the expression for the mass moment of inertia for component 2.
Here, the mass moment of inertia for component 2 is
Write the expression for the mass moment of inertia with respect to centroidal axis.
Write the expression for the centroidal axis from the reference axis.
Write the expression for the mass moment of inertia with respect to centroidal axis.
Here, the mass moment of inertia for component 3 is
Write the expression for the mass moment of inertia for component 3.
Write the expression for the mass of component 2.
Here, the mass of component 2 is
Write the expression for volume of the component 2.
Here, the sides of the component are
Write the expression for the mass of component 3.
Here, the mass of component 3 is
Write the expression for volume of the component 3.
Here, the diameter of the circle is
Write the expression for the distance of the component 3.
Write the expression for the mass moment of inertia with respect to
Write the expression for the mass moment of inertia for component 1.
Here, the mass moment of inertia for component 1 is
Write the expression for the mass moment of inertia with respect to centroidal axis.
Write the expression for the centroidal axis from the reference axis.
Write the expression for the mass moment of inertia for component 2.
Here, the mass moment of inertia for component 2 is
Write the expression for the mass moment of inertia with respect to centroidal axis.
Write the expression for the centroidal axis from the reference axis.
Write the expression for the mass moment of inertia with respect to centroidal axis.
Here, the mass moment of inertia for component 3 is
Write the expression for the mass moment of inertia for component 3.
Write the expression for the distance of the component 3.
Write the expression for the mass moment of inertia with respect to
Write the expression for the mass moment of inertia for component 1.
Here, the mass moment of inertia for component 1 is
Write the expression for the mass moment of inertia with respect to centroidal axis.
Write the expression for the centroidal axis from the reference axis.
Write the expression for the mass moment of inertia for component 2.
Here, the mass moment of inertia for component 2 is
Write the expression for the mass moment of inertia with respect to centroidal axis.
Write the expression for the centroidal axis from the reference axis.
Write the expression for the mass moment of inertia with respect to centroidal axis.
Here, the mass moment of inertia for component 3 is
Write the expression for the mass moment of inertia for component 3.
Write the expression for the distance of the component 3.
Write the expression for the mass moment of inertia with respect to
Write the expression for the mass of component 1.
Here, the mass of component 1 is
Write the expression for the mass moment of inertia for component 1.
Here, the products of the inertia of the body with respect to centroidal axis for component 1 is
Write the expression for the mass moment of inertia for component 1.
Here, the products of the inertia of the body with respect to centroidal axis for component 1 is
Write the expression for the mass moment of inertia for component 1.
Here, the products of the inertia of the body with respect to centroidal axis for component 1 is
Write the expression for the mass of component 2.
Here, the mass of component 2 is
Write the expression for the mass moment of inertia for component 2.
Here, the products of the inertia of the body with respect to centroidal axis for component 2 is
Write the expression for the mass moment of inertia for component 2.
Here, the products of the inertia of the body with respect to centroidal axis for component 2 is
Write the expression for the mass moment of inertia for component 2.
Here, the products of the inertia of the body with respect to centroidal axis for component 2 is
Write the expression for the mass of component 3.
Here, the mass of component 3 is
Write the expression for the mass moment of inertia for component 3.
Here, the products of the inertia of the body with respect to centroidal axis for component 3 is
Write the expression for the mass moment of inertia for component 3.
Here, the products of the inertia of the body with respect to centroidal axis for component 3 is
Write the expression for the mass moment of inertia for component 3.
Here, the products of the inertia of the body with respect to centroidal axis for component 3 is
Write the expression for the mass product of inertia.
Here, the mass product of inertia is
Write the expression for the mass product of inertia.
Here, the mass product of inertia is
Write the expression for the mass product of inertia.
Here, the mass product of inertia is
Write the expression for the volume of the component 1.
Here, the sides of the component is
Write the expression for volume of the component 2.
Here, the sides of the component is
Write the expression for volume of the component 3.
Here, the diameter of the circle is
Calculation:
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
Substitute
The principal mass moment of inertia at the origin is calculated as follows:
After solving above equation,
Conclusion:
The principal mass moment of inertias at the origin are
(b)
The principal axis about the origin.
Answer to Problem B.71P
The principal axis about the origin are
Explanation of Solution
Given information:
The density of the steel is
The following figure represents the given system.
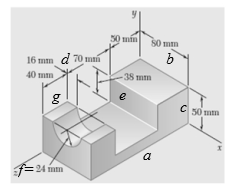
Figure-(1)
Calculation:
The direction cosine is calculated as follows:
Substitute the values from the sub-part (a) in above equations as follows:
After solving above equations,
Direction cosine in x direction is calculated as follows:
Direction cosine in y and z direction are,
So, the direction is calculated as follows:
Again,
The direction cosine is calculated as follows:
Substitute the values from the sub-part (a) in above equations as follows:
After solving above equations,
Direction cosine in x direction is calculated as follows:
Direction cosine in y and z direction are,
So, the direction is calculated as follows:
Similarly,
The direction cosine is calculated as follows:
Substitute the values from the sub-part (a) in above equations as follows:
After solving above equations,
Direction cosine in x direction is calculated as follows:
Direction cosine in y and z direction are,
So, the direction is calculated as follows:
The sketch is shown below:
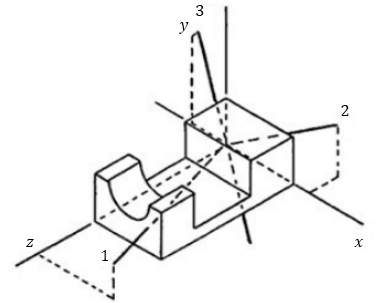
Conclusion:
So, the principal axis about the origin are
Want to see more full solutions like this?
Chapter B Solutions
Vector Mechanics For Engineers
- Determine the product of inertia with respect to the x- and y-axes for the quarter circular, thin ring (tR) by integration.arrow_forwardDetermine the mass products of inertia Ixy, Iyz, and Izx of the cast aluminum machine component shown. (The density of aluminum is 2700 kg/m3.)arrow_forwardDetermine for the quarter ellipse of Prob. 9.67 the moments of inertia and the product of inertia with respect to new axes obtained by rotating the x and y axes about O (a) through 45° counterclockwise, (b) through 30° clockwise.(Reference to Problem 9.67):Determine by direct integration the product of inertia of the given area with respect to the x and y axes.arrow_forward
- Knowing that the thin hemispherical shell shown has a mass m and thickness t , determine the mass moment of inertia and the radius of gyration of the shell with respect to the x axis)Hint: Consider the shell as formed by removing a hemisphere of radius r from a hemisphere of radius r +t ; then neglect the terms containing t2 and t3 and keep those terms containing t.)arrow_forwardDetermine the mass products of inertia Ixy, Iyz, and Izx of the steel fixture shown. (The density of steel is 7850 kg/m3.)arrow_forwardA thin plate with a mass m has the trapezoidal shape shown. Determine the mass moment of inertia of the plate with respect to (a) the centroidal axis CC’ that is perpendicular to the plate, (b) the axis AA’ that is parallel to the x axis and is located at a distance 1.5a from the plate.arrow_forward
- For the component described in the problem indicated, determine (a) the principal mass moments of inertia at the origin, (b) the principal axes of inertia at the origin. Sketch the body and show the orientation of the principal axes of inertia relative to the x, y, and z axes.Prob. 9.141Reference to Problem 9.141:arrow_forwardThe area shown is revolved about the x axis to form a homogeneous solid of revolution of mass m . Determine by direct integration the mass moment of inertia of the solid with respect to (a) the x axis, (b) the y axis. Express your answers in terms of m and the dimensions of the solid.arrow_forwardHello good afternoon, Permission, i have a question in my homework. The following bellow is question. Please advice. Thank you Regards,Irfan Determine the mass moments of inertia and the radii of gyration of the steel machine element shown with respect to the x and y axes. (The density of steel is 7850 kg/m3.arrow_forward
- Determine the mass products of inertia Ixy, Iyz, and Izx of the steel machine element shown. (The density of steel is 7850 kg/m3.)arrow_forwardFor the area indicated, determine the orientation of the principal axes at the origin and the corresponding values of the moments of inertia.Area of Prob. 9.73(Reference to Problem 9.73):Using the parallel-axis theorem, determine the product of inertia of the area shown with respect to the centroidal x and y axes.arrow_forwardA piece of thin, uniform sheet metal is cut to form the machine component shown. Denoting the mass of the component by m , determine its mass moment of inertia with respect to (a) the axis AA,(b) the axis BB ’, where the AA and BB ’ axes are parallel to the x axis and lie in a plane parallel to and at a distance a above the xz plane.arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
