What is Pollard's rho algorithm?
Pollard's rho algorithm, by John Pollard, is used to factorize integers. The expected running time of this algorithm is proportional to the square root of the size of the smallest prime factor of the composite number that is factorized.
Pollard's algorithm is not the fastest. However, it exceeds trial division by several orders of magnitude. It also consumes less space.
Core concept
Pollard's rho algorithm aims to factorize a number n = pq. Here, p is a non-trivial factor. A pseudorandom sequence is created using a polynomial modulo n, called g(x). For instance, let g(x) =(x2 + 1) mod n. Considering the starting value is 2, the following continuous sequence will be generated:
x1 = g(2), x2 = g(g(2)), x3 = g(g(g(2))), and so on.
The above sequence is related to {xk mod p}. Nevertheless, p is not known beforehand, so the sequence cannot be handled explicitly by the algorithm.
Since the number of possible values for the sequence is finite, the sequences { xk} and the {xk mod p} will repeat, even though their values are unknown. If the sequences had been random numbers, according to the birthday paradox, the number of { xk} before repetition would be O(√N), where N is the total number of possible values. In that case, {xk mod p} sequence will repeat earlier than the { xk} sequence. After repetition of the sequence for the first time, the sequence will cycle since each value depends on the value before it. This cycling structure results in the name "rho (Ρ) algorithm" because the nodes in the directed graph form a rho shape when the values of x1 mod p, x2 mod p, ..., are represented.
Floyd's cycle-finding algorithm detects the structure. Consider two nodes, i and j, such that xi and xj. In every step, one node moves to the next node in the sequence, and the following node moves forward by two nodes. Next, check if the greatest common divisor, gcd(xi - xj, n) ≠ 1. If it is not equal to 1, then there is a repetition in the sequence {xk mod p}. This is valid when xi is equal to xj. The difference between the nodes is a multiple of p. This also happens when the gcd is a divisor of n apart from 1.
The Algorithm
The Pollard's rho integer factorization algorithm takes n inputs, the integer to be factorized, and g(x), a polynomial in x computed modulo n. The output of the algorithm is either a non-trivial factor of n or failure. When n is composite, the factor fails. Consequently, the algorithm should be repeated using another value except 2. Below are the steps in Pollard's rho algorithm:
x = 2
y = 2
s = 1
while s = 1:
x = g(x)
y = g(g(y))
s = gcd(|x-y|,n)
if s = n:
return fail
else:
return s
Note: Here, x = xi and y = xj.
Overview of birthday paradox or birthday problem
The birthday paradox or birthday problem deals with the probability that if a set of n random people is selected, there is a probability that two people will have the same birthday. The problem determines that if a group of 23 people is selected, the probability that the birthday of two people falls on the same day is higher than 50%. Similarly, in a group of 70 people, the chances of having a birthday on the same day are 99.9%. For 367 or more people, the chances will exceed 100%.
The concept of the birthday paradox is widely used in a cryptographic attack to reduce the complexity of finding a hash function collision and calculate the risk of hash collision.
Overview of Floyd's cycle-finding algorithm
The cycle-finding or cycle-detection algorithm finds a cycle in a sequence of iterating values in a function. The algorithm is also known as a tortoise and hare algorithm. It states that if a tortoise and hare start moving from one point through the sequence, they will meet at one point despite having different speeds.
The cycle-finding algorithm is used in Pollard's rho algorithm to detect cycles. It is also applied in cryptography to determine collision in a hash function.
Factorization example
Consider the following example to find factors using Pollard's rho algorithm.
Assume n = 8051, g(x) = (x2 + 1) mod 8051
If the starting value of i is 1, it will result in the following values.
| i | x | y | gcd(|x-y|, 8051) |
| 1 | 5 | 26 | 1 |
| 2 | 26 | 7474 | 1 |
| 3 | 677 | 871 | 97 |
| 4 | 7474 | 1481 | 1 |
Here, the non-trivial factor of 8051 will be 97. Alternatively, if x=y=2 is used as the starting value, the non-trivial factor will be 83.
Below is another example of Pollard’s rho algorithm for n = 253 and g(x) = x2 mod 253. Here, the starting value is 2.
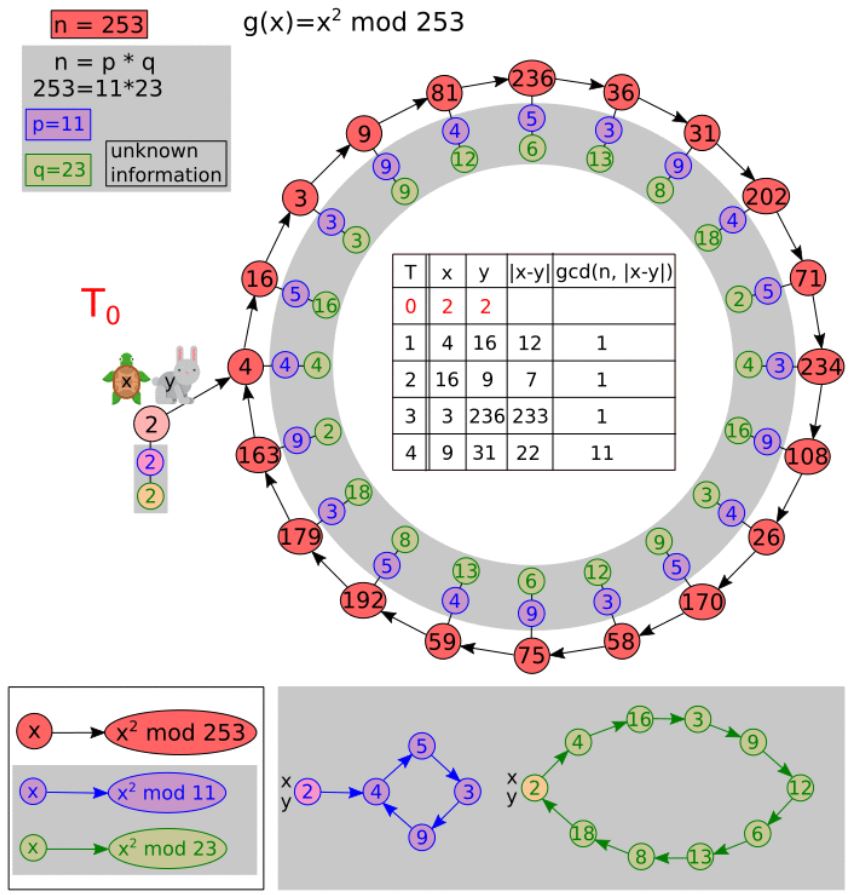
Time complexity
Pollard's rho algorithm gives a trade-off between the running time and probability that identifies a factor. If the algorithm's pseudorandom number x = g(x) is an actual random number, the success would be achieved in half the time according to the birthday paradox. In that case, the iterations would be O(√p ≤ O(4√n). The same analysis is true for the rho algorithm. However, it is only a heuristic claim.
Context and Applications
Pollard's rho algorithm is mainly used in cryptography. It is a concept included in courses such as:
- Bachelors in Science (Cyber Security)
- Masters in Science (Cyber Security)
- Masters in Science (Information Security & Assurance)
Practice Problems
1. Which of the following concepts are not used in Pollard's rho algorithm?
- GCD
- Birthday paradox
- Cycle-detection
- Fermat's method
Answer: Option d
Explanation: Fermat's factorization is a technique used to find factors of integers. It is a separate method and not used in Pollard's algorithm.
2. Pollard rho factorization method works faster in case of which numbers?
- Numbers having small factors
- Numbers having large factors
- Both a and b
- Numbers having multiple prime factors
Answer: Option a
Explanation: Pollard's rho algorithm is very fast for numbers having small factors. However, for numbers having large factors, it is slower.
3. Which of the following shows the time complexity of Pollard's rho algorithm?
- O(n)
- O(n log n)
- O(4√n)
- O(2n)
Answer: Option c
Explanation: According to the analysis, the time complexity of Pollard's rho algorithm is O (4√n).
4. Why is Pollard's rho algorithm used?
- To factorize a given set of integers
- To find prime factor numbers
- To calculation of gcd of prime factors
- To factoring gcd of prime numbers
Answer: Option a
Explanation: Pollard's rho algorithm is an integer factorization algorithm. This indicates that the algorithm is used to find the factors of a set of integers.
5. Which of the following is an application of the birthday problem?
- Finding risk of collision of a hash function
- Computing a gcd equation
- Computing the speed of an algorithm
- Computation the gcd of large numbers
Answer: Option a
Explanation: The birthday problem concept is applied to find the risk of collision of a hash function and reduce the complexity of finding the collision.
Common Mistakes
Students should note that the birthday paradox and cycle detection are not part of Pollard's rho algorithm. Instead, they are concepts that are used in determining factors using Pollard's algorithm.
Related Concepts
- Pollard's rho algorithm for logarithms
- Public key cryptography
- Fermat's factorization method
- Factorization of polynomials
- Greatest common divisor
Want more help with your computer science homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.
Pollard’s rho algorithm Homework Questions from Fellow Students
Browse our recently answered Pollard’s rho algorithm homework questions.
Search. Solve. Succeed!
Study smarter access to millions of step-by step textbook solutions, our Q&A library, and AI powered Math Solver. Plus, you get 30 questions to ask an expert each month.