Deductive Reasoning
In deductive reasoning, conclusions are framed based on previously known facts. It is informally known as top-down logic. This form of reasoning is used when a general statement is declared about an entire class of things and an example is specifically given. If the example fits into the previously mentioned class of things, then deductive reasoning can be used to arrive at a conclusion. Put another way, for deductive reasoning, we take information from two or more statements and draw a logically sound conclusion. A classic example is:
All men are mortal.
Brian is a man.
Therefore, Brian is mortal.
Deductive Reasoning in Geometry
Refer to the figure given below and identify which of the following statements are correct.

As per given data, is present on both Line A and Line B. That is, it is a corresponding angle. Since it is on the same side of the transversal line C, Line A is parallel to Line B. Statement 1 is true.
and form a pair of alternate angles. Hence . Statement 2 is true.
If , the only way for Statement 3 to be correct is when . Since that is not the case in the given figure Statement 3 is false.
form a linear pair. Their sum always equals 180⁰. Therefore,. Statement 4 is true.
Inductive Logic
In inductive reasoning, a conclusion is drawn based on a given set of patterns. For example, identify the missing terms in the given sequence: .
This is the very well-known Fibonacci series, wherein the next term in a sequence is a sum of the previous two terms. With that information, the missing terms will be calculated as:
5 + 8 = 13
8 + 13 = 21
13 + 21 = 34
Inductive reasoning can also be used to identify definitions.
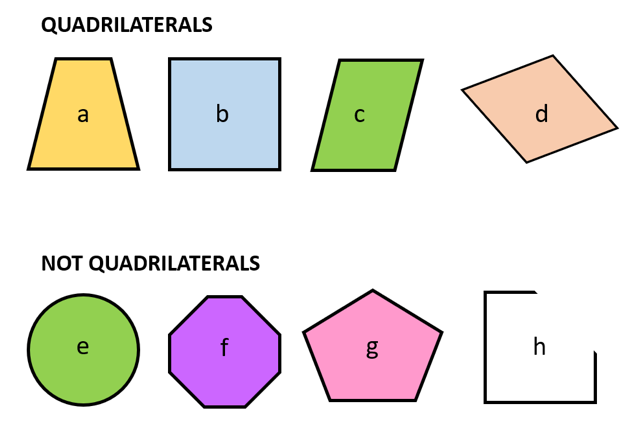
Look at the shapes a, b, c, d which have been classified as “quadrilaterals”. Also observe the shapes e, f, g, h, which are classified as “not quadrilaterals”. With the given data, can we define what a quadrilateral is?
From shapes a, b, c, d we can say that a quadrilateral is a shape that has four sides. The four sides do not need to be of the same length, nor do they always need to be parallel to each other. However, with that statement, shape h also classifies as a quadrilateral. Why is shape h not included in the set of quadrilaterals? Although shape h has four sides, it is not a closed shape. Hence, we can conclude that a quadrilateral is a closed polygon with four sides.
The Difference Between Deductive and Inductive Reasoning

In inductive reasoning, we make specific observations and draw a general conclusion based on the pattern observed. For example: identify the shapes in the given sequence:

As the number progresses, the number of sides of the shape also progress. Hence, the missing figure will be a polygon with five sides. But there is no certainty on the length of the sides of the pentagon. Will it be a regular or irregular pentagon? All we know is that the sixth figure will have five sides.
A good example of where inductive reasoning can fail:
- Questions in every term exam have been easy.
- Therefore, the next term exam will be easy.
It cannot be predicted that the coming term exam will be easy just because the previous one was easy. Hence, the results obtained using inductive reasoning cannot always be relied upon with certainty.
Contrastingly, in deductive reasoning, as the conclusions are derived based on previously known facts, they can be relied upon. For example:
- All numbers ending in 0 or 5 are divisible by 5.
- The number 65 ends with a 5.
- Therefore, it must be divisible by 5.
However, at times even deductive reasoning can fail with two given facts. For example:
- All teachers use a blackboard and chalk.
- Blake uses a whiteboard and a marker.
- Therefore, Blake is not a teacher.
- All marathon runners are tall.
- Charlie is short.
- Therefore, Charlie is not a marathon runner.
For deductive reasoning to give a valid deduction, the statements upon which the conclusions are being drawn need to be true. Only when the statements are accurate will the conclusion be correct.
Deductive and Inductive Reasoning Summary
| Inductive Reasoning | Deductive Reasoning |
|---|---|
| The first pen I pulled from my bag is blue. The second pen I pulled from my bag is red. Therefore, all the pens in my bag are red or blue. | The first pen I pulled from my bag is blue. All pens in my bag are blue. Therefore, the second pen I pull from my bag will be blue too. |
| My father is German. He has blond hair. Therefore, everyone from Germany has blond hair. | My father is German. Everyone from Germany has blond hair. Therefore, my father has blond hair. |
| Scooby is a therapy dog. He is happy. All therapy dogs are happy. | Scooby is a therapy dog. All therapy dogs are happy. Therefore, Scooby is happy. |
In the above shown comparison, each example of deductive reasoning is more convincing than inductive reasoning when we assume that the first two statements are true. We cannot say that the conclusions derived from inductive reasoning are necessarily false, but they lack the supporting evidence to be accepted as a universal truth.
Related Solutions on bartleby
Want more help with your calculus homework?
*Response times may vary by subject and question complexity. Median response time is 34 minutes for paid subscribers and may be longer for promotional offers.
Deductive Reasoning in Math Homework Questions from Fellow Students
Browse our recently answered Deductive Reasoning in Math homework questions.