What is Spring Potential Energy? 

The potential energy is the energy possessed by a body by virtue of its position or the energy held by the object due to its position relative to other objects, its force like stresses, charge, and other factors affecting the particles of the body. The potential energy is the measure of the net work done by or on the body. The spring potential energy is the potential energy stored due to the deformation of an elastic spring and this elasticity is due to the stretched spring. The elasticity is the ability of a solid-state matter to come back to its equilibrium position or original position after any kind of external force is acted on it. It is also known as Elastic potential energy. The potential energy here is caused due to the displacement of the spring from its equilibrium position to another position and this potential energy is equal to the net work done due to the stretching of the spring. It also resembles the same mechanics of the oscillation of a simple pendulum, where due to the external force, the object moves from its equilibrium position to its maximum ends and the periodic motion continues till it comes back to the equilibrium position to rest.  

An ideal spring may undergo compression and expansion, so the force applied will be in its opposite direction. The spring is generally considered to be ideal, which means masses in its equilibrium position and when it is made to stretch, there will be a displacement from its equilibrium. So the stretched distance's value will be negative.  

Hooke's Law

Hooke's law states that the force required to stretch the spring will be directly proportional to the amount of stretch or the displacement of the string from its equilibrium. The mathematical equation that explains Hookes' law is 

F= k·x 

Here F is the force applied to stretch the spring, k is the constant known as spring constant and x is the displacement. The law can also be stated as F is the restoring force that the spring exerts to come back to its equilibrium position. In that case, we have a negative sign : 

F= -kx 

The Equation Formulation of the Work done by the Spring 

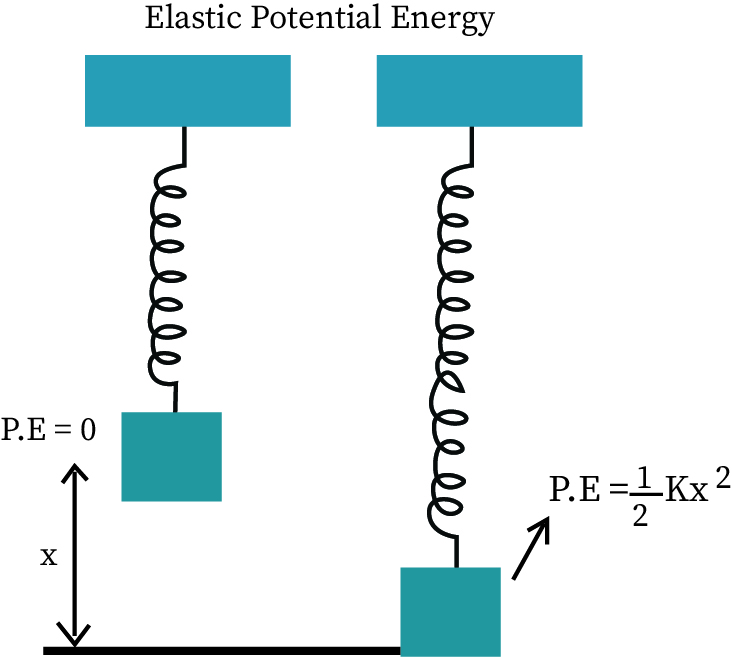
The work done in stretching the aspring from equilibrium to a position x, gets stored in the spring as spring potential energy. It can be derived as below, using the force equation from Hooke’s Law, 

$\begin{array}{c}W={\displaystyle \int F.dx}\\ ={\displaystyle \underset{0}{\overset{x}{\int }}kx}.dx\\ =k{\displaystyle \underset{0}{\overset{x}{\int }}x.dx}\\ =k.\frac{x^2}{2}\\ =\frac{1}{2}k{x}^2\end{array}$

Thus the spring potential energy is U_s = ½ kx² .(Let the spring potential energy be U_s). Now if the graph is plotted to understand the force and displacement relation, they both are perpendicular to each other and the spring constant will be at 45 degrees to both the components, hence in the graph, it forms like a right angle triangle. So the base of the right angle triangle is the product of displacement and spring constant and the height is also the displacement. If x is the displacement and k is the spring constant, then by calculating the equation it comes to  U_s = 1/2·k·x² 

Hence the work done by the spring will be equal to the difference between the final and initial potential energies. So it can be denoted by DU. The potential energy of the spring will be zero when it is in the equilibrium position. When the spring is stretched the potential energy increases. Then at maximum potential energy points, its kinetic energy would be zero.   

NOTE: The value of the spring's potential energy cannot be negative irrespective of the restoring spring force and its negative sign. 

Application of Spring's Potential Energy 

1) The spring potential energy is used in various applications in plenty of mechanical devices. The feature of the compression and expansion of the spring adds an advantage to it. The springs are used in plenty of automobiles as a shock absorber and in regenerative braking systems. 

2) The potential energy of the springs is also used in control system application and its capacity to store makes it more efficient. 

3) It is also used in manufacturing of certain guns where due to the compression of the spring and its ability to store the elastic potential energy, when the gun's trigger is pulled, then these springs apply a force and hence there is recoil.  

4) The real life application of elasticity is also seen in using the rubber band, pole vault poles and in trampolines. 

Practice Problems 

1) If a spring extends by x on loading, then calculate the  energy stored in the spring. Let T be the spring force and K is a force constant 

a) 2x/T²  b) T²/2k c)2k/T² d) T²/2x 

Answer: When the spring extends a restoring force is developed in it, which depends on the deflection in the spring. The magnitude of this force is given as

The energy stored in the spring is given as

Rearrange the equation of the force and substitute the expression of the deflection in the formula of the energy to calculate its value.

The correct option is (b).

2) Determine the potential energy of a spring having a spring constant as 200 Nm^-1 and the displacement is 0.8 m 

Answer: The formula to calculate the potential energy of the given spring is

The given values of the spring constant and the deflection are 200 Nm^-1 and 0.8 m respectively. Substitute the values to calculate potential energy.

The energy is 64 Joules.

3) An engineer attaches a spring to a sterdy wooden board. Let the board be placed horizontally on a table. The spring uses an energy value of three joules to stretch and the displacement moved by the spring is 99 cm. What will be the value of the spring constant using the equation of the spring's potential energy ? 

Answer: The formula to calculate the potential energy of the given spring is 

The displacement and energy in the spring is given as 99 cm and 3 Joules. Substitute the values in the formula and calculate the value of the spring’s constant.

This is the given value of the spring constant.

4) A person wants to do an experiment with the spring and analyze the potential energy of the spring. So the person attaches one end of the spring to a metallic board and the other end is free, so the spring can be expanded or compressed. The person pulls the string having a spring constant of 100 Netwon per meter and stretches it from a distance of 0.20 meters to 0.40 meters. Determine the value of the spring's potential energy 

The formula to calculate the potential energy of the given spring is

It is given that the value of the spring constant is 100 Nm^-1, final displacement is 0.40 m and initial displacement is 0.20 m. Substitute the values to calculate the value of the energy of the spring.

$$\begin{array}{l}E=\frac{1}{2}100{\text{ Nm}}^{-1}{\left(0.40\text{ m - 0}\text{.20 m}\right)}^2\\ E=2\text{ J}\end{array}$$

The energy is 2 J.

Context and Applications    

This topic is significant in the professional exams for both undergraduate and graduate courses, especially for  

• Bachelors in Science (Physics)  
• Masters in Science (Physics)