
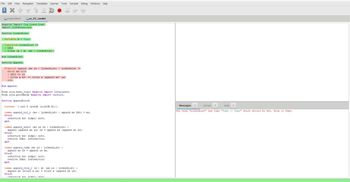
Can you Fix this error in the following image
Require Import Coq.Lists.List.
Import ListNotations.
Section LinkedList.
Variable A : Type.
Inductive LinkedList :=
| LNil
| LCons (x : A) (xs : LinkedList).
End LinkedList.
Section Append.
Fixpoint append (xs ys : LinkedList) : LinkedList :=
match xs with
| LNil => ys
| LCons x xs' => LCons x (append xs' ys)
end.
End Append.
From iris.base_logic Require Import invariants.
From iris.proofmode Require Import tactics.
Section AppendProof.
Context `{!inG Σ (authR (listUR A))}.
Lemma append_nil_r (xs : LinkedList) : append xs LNil = xs.
Proof.
induction xs; simpl; auto.
Qed.
Lemma append_assoc (xs ys zs : LinkedList) :
append (append xs ys) zs = append xs (append ys zs).
Proof.
induction xs; simpl; auto.
rewrite IHxs. reflexivity.
Qed.
Lemma append_comm (xs ys : LinkedList) :
append xs ys = append ys xs.
Proof.
induction xs; simpl; auto.
rewrite IHxs. reflexivity.
Qed.
Lemma append_cons_r (x : A) (xs ys : LinkedList) :
append xs (LCons x ys) = LCons x (append xs ys).
Proof.
induction xs; simpl; auto.
Qed.
End AppendProof.
Step by stepSolved in 2 steps

- How is an array stored in main memory? How is a linked list stored in main memory? What are their comparative advantages and disadvantages? Give examples of data that would be best stored as an array and as a linked list.arrow_forwardWrite an Add method that adds the contents of the decPrice variable to the lstPrices control.arrow_forwardAttempt to view the structure of the HOMEWORK13 view.arrow_forward
 New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning
New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning EBK JAVA PROGRAMMINGComputer ScienceISBN:9781337671385Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK JAVA PROGRAMMINGComputer ScienceISBN:9781337671385Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning Programming with Microsoft Visual Basic 2017Computer ScienceISBN:9781337102124Author:Diane ZakPublisher:Cengage LearningProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage
Programming with Microsoft Visual Basic 2017Computer ScienceISBN:9781337102124Author:Diane ZakPublisher:Cengage LearningProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage





