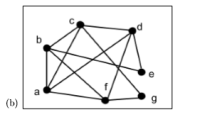
For each graph below, find an Euler circuit in the graph or explain why the graph does not have an Euler circuit. Figure 10: An undirected graph has 7 vertices, a through g. 5 vertices are in the form of a regular pentagon, rotated 90 degrees clockwise. Hence, the top vertex becomes the rightmost vertex. From the bottom left vertex, moving clockwise, the vertices in the pentagon shape are labeled: a, b, c, e, and f. Vertex d is above vertex e, below and to the right of vertex c. Vertex g is below vertex e, above and to the right of vertex f. Undirected edges, line segments, are between the following vertices: a and b; a and c; a and d; a and f; b and f; b and c; b and e; c and d; c and g; d and e; d and f; and f and g

QUESTION 20 Choose the true statement for the following graph. A B D E Oa. The graph has an Euler circuit. Ob. The graph has an Euler path. Oc. The graph has neither an Euler circuit nor an Euler path. Od. The graph has both an Euler circuit and an Euler path.

For each graph below, find an Euler trail in the graph or explain why the graph does not have an Euler trail.(Hint: One way to find an Euler trail is to add an edge between two vertices with odd degree, find an Euler circuit in the resulting graph, and then delete the added edge from the circuit.) Figure 12: An undirected graph has 6 vertices, a through f. 5 vertices are in the form of a regular pentagon, rotated 90 degrees clockwise. Hence, the top vertex becomes the rightmost vertex. From the bottom left vertex, moving clockwise, the vertices in the pentagon shape are labeled: a, b, c, e, and f. Vertex d is above vertex e, below and to the right of vertex c. Undirected edges, line segments, are between the following vertices: a and b; a and c; a and d; a and f; b and f; b and c; b and e; c and d; d and e; and d and f. Edges c f, a d, and b e intersect at the same point.

Explain why the graph does or does not have an Euler circuit. If it does, specify the nodes within the circuit Figure 9: An undirected graph has 7 vertices, a through g. 5 vertices are in the form of a regular pentagon, rotated 90 degrees clockwise. Hence, the top vertex becomes the rightmost vertex. From the bottom left vertex, moving clockwise, the vertices in the pentagon shape are labeled: a, b, c, e, and f. Vertex d is above vertex e, below and to the right of vertex c. Vertex g is below vertex e, above and to the right of vertex f. Undirected edges, line segments, are between the following vertices: a and b; a and c; a and f; b and f; b and c; c and d; c and g; d and e; d and f; and f and g.