Computer Networking: A Top-Down Approach (7th Edition)
7th Edition
ISBN: 9780133594140
Author: James Kurose, Keith Ross
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Related questions
Question
Please help with the program below. Need to write a program called dfs-stack.py in python that uses the algorithm below without an agency list but instead uses an adjacency matrix. The program should prompt the user for the number of vertices V, in the graph.Please read the directions below I will post a picture of the instructions and the algorithm.
![**Algorithm 2.3: Graph Depth-First Search with a Stack**
This algorithm describes the process of performing a depth-first search (DFS) on a graph using a stack.
**StackDFS(G, node) → visited**
- **Input:**
- \( G = (V, E) \), a graph
- `node`, the starting vertex in \( G \)
- **Output:**
- `visited`, an array of size \(|V|\) such that `visited[i]` is `TRUE` if we have visited node \( i \), `FALSE` otherwise
**Procedure:**
1. \( S \leftarrow \text{CreateStack()} \)
2. `visited` \(\leftarrow \text{CreateArray}(|V|) \)
3. For \( i \leftarrow 0 \) to \(|V|\) do
1. `visited[i]` \(\leftarrow \text{FALSE}\)
4. `Push(S, node)`
5. While not `IsStackEmpty(S)` do
1. \( c \leftarrow \text{Pop}(S) \)
2. `visited[c]` \(\leftarrow \text{TRUE}\)
3. For each \( u \) in `AdjacencyList(G, c)` do
- If not `visited[u]` then
- `Push(S, u)`
6. Return `visited`
### Explanation:
- The algorithm initializes a stack \( S \) and a `visited` array.
- It sets all values in the `visited` array to `FALSE`.
- The starting node is pushed onto the stack.
- The algorithm iterates as long as the stack is not empty:
- It pops an element from the stack, marks it as visited, and then pushes its adjacent nodes (if not already visited) onto the stack.
- The process continues until all reachable nodes are visited.
- Finally, the `visited` array is returned, indicating which nodes have been visited.](https://content.bartleby.com/qna-images/question/691d33e1-8c25-4f84-bfa0-1a093fc94f94/b477c839-22e9-44c1-a636-0503ce154826/w2vlfz9_processed.jpeg)
Transcribed Image Text:**Algorithm 2.3: Graph Depth-First Search with a Stack**
This algorithm describes the process of performing a depth-first search (DFS) on a graph using a stack.
**StackDFS(G, node) → visited**
- **Input:**
- \( G = (V, E) \), a graph
- `node`, the starting vertex in \( G \)
- **Output:**
- `visited`, an array of size \(|V|\) such that `visited[i]` is `TRUE` if we have visited node \( i \), `FALSE` otherwise
**Procedure:**
1. \( S \leftarrow \text{CreateStack()} \)
2. `visited` \(\leftarrow \text{CreateArray}(|V|) \)
3. For \( i \leftarrow 0 \) to \(|V|\) do
1. `visited[i]` \(\leftarrow \text{FALSE}\)
4. `Push(S, node)`
5. While not `IsStackEmpty(S)` do
1. \( c \leftarrow \text{Pop}(S) \)
2. `visited[c]` \(\leftarrow \text{TRUE}\)
3. For each \( u \) in `AdjacencyList(G, c)` do
- If not `visited[u]` then
- `Push(S, u)`
6. Return `visited`
### Explanation:
- The algorithm initializes a stack \( S \) and a `visited` array.
- It sets all values in the `visited` array to `FALSE`.
- The starting node is pushed onto the stack.
- The algorithm iterates as long as the stack is not empty:
- It pops an element from the stack, marks it as visited, and then pushes its adjacent nodes (if not already visited) onto the stack.
- The process continues until all reachable nodes are visited.
- Finally, the `visited` array is returned, indicating which nodes have been visited.
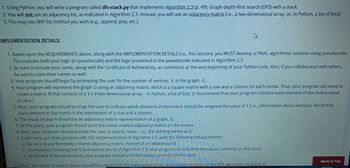
Transcribed Image Text:### Educational Resource: Implementing Graph Depth-First Search (DFS) in Python
#### Instructions
1. **Objective**: You will create a Python program named `dfs-stack.py` to implement Algorithm 2.3, which performs a graph depth-first search (DFS) using a stack.
2. **Requirements**:
- Avoid using an adjacency list as in Algorithm 2.3.
- Instead, utilize an adjacency matrix (a two-dimensional array or a list of lists in Python).
- You can use any list methods (e.g., `append`, `pop`).
#### Implementation Details:
1. **Algorithm Development**:
- Create a complete algorithmic solution using pseudocode. Integrate the logic provided in Algorithm 2.3.
2. **Code Documentation**:
- Include your name and a Certificate of Authenticity as comments at the start of your Python code. Acknowledge any collaborators.
3. **User Interaction**:
- Prompt the user for the number of vertices, `V`, in the graph, `G`.
4. **Graph Representation**:
- Represent `G` using an adjacency matrix: a square matrix with a row and column for each vertex.
- Initialize a matrix `M` of dimensions V x V, using zero for each element initially.
5. **Matrix Population**:
- Allow the user to specify which elements in the matrix should have a value of 1, indicating connections between vertices.
6. **Matrix Display**:
- After creating the adjacency matrix, print it for the user.
7. **Node Selection**:
- Prompt the user to specify the starting vertex in `G`.
8. **Algorithm Implementation**:
- Implement Algorithm 2.3, using the adjacency matrix.
- Print the values on the stack during execution.
- Print values on the stack at the end of the white block in the algorithm.
By executing step 8, you will display how the stack evolves during your implementation of the DFS algorithm on graph `G`.
Expert Solution
arrow_forward
Step 1
Python Code
#It uses a Python dict for easiness
graphDFS = {
'1': ['4', '6'],
'5': ['1', '9'],
'9': ['5'],
'4': [],
'6': ['1', '2'],
'2': []
}
vertexSeen = set() # Tracks the vertexSeen nodes of graphDFS.
def dfs(vertexSeen, graphDFS, node): #DFS function
if node not in vertexSeen:
print(node)
vertexSeen.add(node)
for neighbour in graphDFS[node]:
dfs(vertexSeen, graphDFS, neighbour)
# Driver Code
print("Following is the Depth-First Search")
dfs(vertexSeen, graphDFS, '5')
Step by stepSolved in 2 steps with 1 images
Knowledge Booster
Similar questions
- Which of the following is the correct syntax to construct an ArrayList to store integers? (enter just the letter indicating your selection) a. ArrayList list = new ArrayList(); b. ArrayList[int] list = new ArrayList[int](); c. ArrayList list<integer> = new ArrayList<integer>(); d. ArrayList<Integer> list = new ArrayList(); e. ArrayList<Integer> list = new ArrayList<Integer>(); Your response: [choice]arrow_forwardthe number of edges in a complete 2 of 2 undirected graph of 80 vertices is.? Select one: a. exactly equals 3160 b. None c. less than or equals 3160 d. less than or equals 6320 e. exactly equals 6320 Assume that you have a doubly link list. Pointer x is pointing to the last node in the link list and pointer y is pointing to before the last node. which of the following will remove the node pointed by x from the list? Select one: O a. delete x; b. y->prev->next = y->next; X->prev= y->prev; delete x; O C. X->prev->next = x->next; y->prev= x->prev; delete x; O d. x->next = y; y->prev = x->prev; delete x;arrow_forwardIn this problem you will implement a function called triangle_countwhich will take as input a graph object G, representing an undirectedgraph G, and will return the number of triangles in G. Do not use anyimports for this problem. To simplify the problem you may assume thateach edge is stored twice in G. That is if an edge goes from u to v then vwill be in u’s collection and u will be in v’s collection. If you would prefer,you may assume that an edge is only stored once. In either case G willneed to be regarded as undirected.arrow_forward
- The implementations of the methods addAll, removeAll, retainAll, retainAll, containsAll(), and toArray(T[]) are omitted in the MyList interface. Implement these methods. Use the template at https://liveexample.pearsoncmg.com/test/Exercise24_01_13e.txt to implement these methods this the code i have for the write your own code part import java.util.Iterator; interface MyList<E> extends java.util.Collection<E> { void add(int index, E e); boolean contains(Object e); E get(int index); int indexOf(Object e); int lastIndexOf(E e); E remove(int index); E set(int index, E e); void clear(); boolean isEmpty(); Iterator<E> iterator(); boolean containsAll(java.util.Collection<?> c); boolean addAll(java.util.Collection<? extends E> c); boolean removeAll(java.util.Collection<?> c); boolean retainAll(java.util.Collection<?> c); Object[] toArray(); <T> T[] toArray(T[] a); int size();} and its…arrow_forwardHelp in C++ please: Write a program (in main.cpp) that: Prompts the user for a filename containing node data. Outputs the minimal spanning tree for a given graph. You will need to implement the createSpanningGraph method in minimalSpanTreeType.h to create the graph and the weight matrix. There are a few tabs: main.cpp, graphType.h, linkedList.h, linkedQueue.h, queueADT.h, minimalSpanTreeType.h, and then two data files labeled: CH20_Ex21Data.txt, CH20Ex4Data.txtarrow_forwardWrite a program (in main.cpp) that: Prompts the user for a filename containing node data. Outputs the minimal spanning tree for a given graph. You will need to implement the createSpanningGraph method in minimalSpanTreeType.h to create the graph and the weight matrix. Note: Files Ch20_Ex21Data.txt and Ch20_Ex4Data.txt contain node data that you may test your program with. minimalSpanTreeType.h : #ifndef H_msTree #define H_msTree #include <iostream> #include <fstream> #include <iomanip> #include <cfloat> #include "graphType.h" using namespace std; class msTreeType: public graphType { public: void createSpanningGraph(); //Function to create the graph and the weight matrix. //Postcondition: The graph using adjacency lists and // its weight matrix is created. void minimalSpanning(int sVertex); //Function to create a minimal spanning tree with //root as sVertex. // Postcondition: A minimal spanning…arrow_forward
- Background: When searching for an item in a list, each item that we examine (compare) is considered to be interrogated. If we search for John, the following names are interrogated: Harry, Larry, John (in that order). If two names tie for the middle position, choose the first of the two names for the middle.If we search this same list for John using the Sequential search we would interrogate all the names from Alice through John. We would start with Alice, move to Bob, move to Carol and so forth until we reached John. Directions: Use the original list of names (Alice - Oliver) to answers questions 1-8. Using a sequential search, what names are interrogated to find Carol? Using a sequential search, what names are interrogated to determine that Sam is not in the list? Using a binary search, what names are interrogated to find Carol? Using a binary search, what names are interrogated to determine that Sam is not in the list? Will a binary search or sequential search find Alice…arrow_forwardGiven a large number represented in the form of a linked list. Write code to increment the number by 1 in-place(i.e. without using extra space). Note: You don't need to print the elements, just update the elements and return the head of updated LL. Input Constraints: 1 <= Length of Linked List <=10^6. Input format : Line 1 : Linked list elements (separated by space and terminated by -1) Output Format : Line 1: Updated linked list elements Sample Input 1 : 3 9 2 5 -1 Sample Output 1 : 3 9 2 6 Sample Input 2 : 9 9 9 -1 Sample Output 1 : 1 0 0 0 Solutions://///////// /*************** * Following is the Node class already written class LinkedListNode<T> { T data; LinkedListNode<T> next; public LinkedListNode(T data) { this.data = data; } } ***************/ public class Solution { public static LinkedListNode<Integer>…arrow_forwardPython question please include all steps and screenshot of code. Also please provide a docstring, and comments throughout the code, and test the given examples below. Thanks. Suppose that you are given a list of strings representing a deck of 52 cards. Write afunction called bridgeHands() which takes the list as its only parameter. It shuffles the listand divides it into 4 hands (tuples) of 13 cards each. It returns a dictionary in which thekeys are the strings 'North', 'South', 'East', and 'West', with each key corresponding to adifferent one of the hands.arrow_forward
- Java Programming language Help please.arrow_forwardSorting Create a MyLinkedList class with inner Node class, data fields, and the insert(element) method. Implement a toString method to return all nodes in MyLinkedList. Implement a recursive sorting and a non-recursive sorting method.arrow_forwardFind out what happens when you just leave the stack alone.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
- Computer Networking: A Top-Down Approach (7th Edi...Computer EngineeringISBN:9780133594140Author:James Kurose, Keith RossPublisher:PEARSON
Computer Organization and Design MIPS Edition, Fi...Computer EngineeringISBN:9780124077263Author:David A. Patterson, John L. HennessyPublisher:Elsevier Science
Network+ Guide to Networks (MindTap Course List)Computer EngineeringISBN:9781337569330Author:Jill West, Tamara Dean, Jean AndrewsPublisher:Cengage Learning 
Concepts of Database ManagementComputer EngineeringISBN:9781337093422Author:Joy L. Starks, Philip J. Pratt, Mary Z. LastPublisher:Cengage Learning
Prelude to ProgrammingComputer EngineeringISBN:9780133750423Author:VENIT, StewartPublisher:Pearson Education
Sc Business Data Communications and Networking, T...Computer EngineeringISBN:9781119368830Author:FITZGERALDPublisher:WILEY
Computer Networking: A Top-Down Approach (7th Edi...
Computer Engineering
ISBN:9780133594140
Author:James Kurose, Keith Ross
Publisher:PEARSON
Computer Organization and Design MIPS Edition, Fi...
Computer Engineering
ISBN:9780124077263
Author:David A. Patterson, John L. Hennessy
Publisher:Elsevier Science
Network+ Guide to Networks (MindTap Course List)
Computer Engineering
ISBN:9781337569330
Author:Jill West, Tamara Dean, Jean Andrews
Publisher:Cengage Learning
Concepts of Database Management
Computer Engineering
ISBN:9781337093422
Author:Joy L. Starks, Philip J. Pratt, Mary Z. Last
Publisher:Cengage Learning
Prelude to Programming
Computer Engineering
ISBN:9780133750423
Author:VENIT, Stewart
Publisher:Pearson Education
Sc Business Data Communications and Networking, T...
Computer Engineering
ISBN:9781119368830
Author:FITZGERALD
Publisher:WILEY