Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Related questions
Question
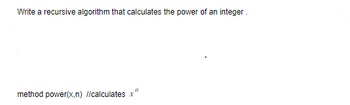
Transcribed Image Text:**Title:** Implementing a Recursive Algorithm to Calculate the Power of an Integer
**Introduction:**
This educational article describes how to write a recursive algorithm to compute the power of an integer. The algorithm is designed to calculate \( x^n \), where \( x \) is the base and \( n \) is the exponent.
**Algorithm Methodology:**
- **Method Signature:** `power(x, n)`
This method is a recursive function that determines the value of \( x \) raised to the power of \( n \). As a fundamental principle of recursion, the function must include a base case to avoid infinite recursion and correctly compute the result.
**Recursive Function Explanation:**
- **Base Case:**
The base case will usually check if the exponent \( n \) is equal to zero. In this situation, any non-zero base raised to the power of zero equals one, i.e., \( x^0 = 1 \).
- **Recursive Case:**
If \( n \) is not zero, the function should call itself with modified parameters in a manner that progresses towards the base case. Typically, this involves multiplying the base \( x \) by the result of `power(x, n-1)`.
Through this recursive breakdown, the problem gradually simplifies until it resolves to the base case, at which point the algorithm assembles the results to return the computed power.
**Conclusion:**
Understanding how to implement a recursive algorithm for calculating powers introduces fundamental concepts of recursion and base cases. This recursive approach is an efficient way to solve exponentiation problems, especially for applying mathematical calculations in computer science.
**Note:** While recursion provides a clear and efficient solution, always ensure to consider the implications of stack depth and memory constraints with larger exponents.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step by stepSolved in 2 steps with 2 images
Knowledge Booster
Similar questions
- What is the nearest neighbor algorithmarrow_forwardCarry out all the steps in the the Euclidean algorithm for 260 and 210 as we did in class. This means find the greatest common divisor according to this algorithm. You may put spaces or no spaces around all plus (+ ), minus ( - ), equal ( = ), or multiplication ( * ) signs you use. If you get a zero ot some point do not leave it out. Each line should be a complete mathematical equation.arrow_forwardApply the backflow algorithm to the digraph below T9 (6) T5 (12) T1 (3) T6 (10) T8 (4) T10 (5) Т2 (2) End ТЗ (8) T7 (9) T4 (11) Task 5 has a critical time of Task 2 has a critical time ofarrow_forward
- Information about ocean weather can be extracted from radar returns with the aid of a special algorithm. A study is conducted to estimate the difference in wind speed as measured on the ground and via the Seasat satellite. To do so, wind speeds (miles per hour) are measured on the ground and via the Seasat satellite simultaneously at 12 special times. The data is shown in the following table. The table also shows the difference between the wind speed on the ground and that via the Seasat satellite at each time, as well as some summary statistics. Difference Time Ground (x) Satellite (y) d = x – y 1 4.46 4.08 0.38 3.99 3.94 0.05 3.73 5.00 -1.27 4 3.29 5.20 -1.91 4.82 3.92 0.90 6. 6.71 6.21 0.50 7 4.61 5.95 -1.34 8 3.87 3.07 0.80 9. 3.17 4.76 -1.59 10 4.42 3.25 1.17 11 3.76 4.89 -1.13 12 3.30 4.80 -1.50 d = -0.41 Sd = 1.14arrow_forward4. [Ocean Weather] Information about ocean weather can be extracted from radar returns with the aid of a special algorithm. A study is conducted to estimate the difference in wind speed as measured on the ground and via the Seasat satellite. To do so, wind speeds (miles per hour) are measured on the ground and via the Seasat satellite simultaneously at 12 special times. The data is shown in the following table. The table also shows the difference between the wind speed on the ground and that via the Seasat satellite at each time, as well as some summary statistics. Difference Time Ground (x) Satellite (y) d= x – y 1 4.46 4.08 0.38 3.99 3.94 0.05 3 3.73 5.00 -1.27 4 3.29 5.20 -1.91 4.82 3.92 0.90 6 6.71 6.21 0.50 7 4.61 5.95 -1.34 8. 3.87 3.07 0.80 3.17 4.76 -1.59 10 4.42 3.25 1.17 11 3.76 4.89 -1.13 12 3.30 4.80 -1.50 d = -0.41 Sd = 1.14 It is claimed that the wind speed measured on the ground is lower than that measured via the Satellite on average. Set up your hypotheses to test this…arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
- Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY 
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated
Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY
Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,