
Concept explainers
Starting with Equations
Derive the equation of force and moment coefficients with the help of given equations.
Explanation of Solution
Given:
The equation of normal force is,
The equation of axial force is,
The equation of the moment about leading edge per unit span is,
Here, pu and pl is the pressure upper and below the surface of the body and
Calculation:
The calculation for coefficient of normal force (1.15) is as follows:
The equation of normal force is
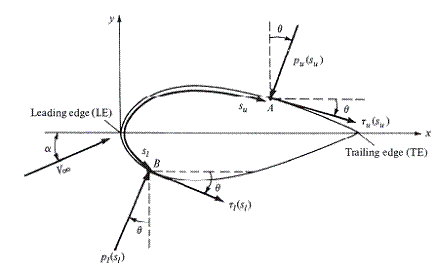
Fig:
Nomenclature for the integration of pressure and shear stress distributions over a two-dimensional body surface.
From figure:
Then, normal force per unit span is
Now, divide by
Here,
Normal force coefficient
Pressure coefficient
Skin friction coefficient
Thus, the equation can be written as:
Now the calculation for coefficient of axial force (1.16) is as follows:
The equation of axial force is
From figure:
Then,
Divide by
Here,
Axial force coefficient
Pressure coefficient
Skin friction coefficient
Then, the above equation can be written as:
And, the calculation for coefficient of moment force (1.17) is as follows:
The equation of the moment about leading edge per unit span is,
Divide by
Here,
Coefficient of moment
Pressure coefficient
Skin friction coefficient
Then, the above equation can be written as:
Want to see more full solutions like this?
Chapter 1 Solutions
Fundamentals of Aerodynamics
- Solve the following problem and show your complete solutions. explain your answer for better understandingarrow_forwardSolve the following problem and show your complete solutions for better understanding.arrow_forwardOne of your employees is complaining of knee pain on the R. While assessing his workstation, you noted that from a sitting position (starting position: 90 deg flexion), the employee needs to exert a lot of effort to extend his right knee to 45 deg from the starting point. The length of the limb (from the tibial tuberosity to the heel area) is measured to be 38 cm. What now is the linear distance traveled by the limb from the initial position to 45 degrees of knee extension?arrow_forward
 Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press
Elements Of ElectromagneticsMechanical EngineeringISBN:9780190698614Author:Sadiku, Matthew N. O.Publisher:Oxford University Press Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON
Mechanics of Materials (10th Edition)Mechanical EngineeringISBN:9780134319650Author:Russell C. HibbelerPublisher:PEARSON Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education
Thermodynamics: An Engineering ApproachMechanical EngineeringISBN:9781259822674Author:Yunus A. Cengel Dr., Michael A. BolesPublisher:McGraw-Hill Education Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY
Control Systems EngineeringMechanical EngineeringISBN:9781118170519Author:Norman S. NisePublisher:WILEY Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY
Engineering Mechanics: StaticsMechanical EngineeringISBN:9781118807330Author:James L. Meriam, L. G. Kraige, J. N. BoltonPublisher:WILEY





