
Elementary Geometry For College Students, 7e
7th Edition
ISBN: 9781337614085
Author: Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher: Cengage,
expand_more
expand_more
format_list_bulleted
Textbook Question
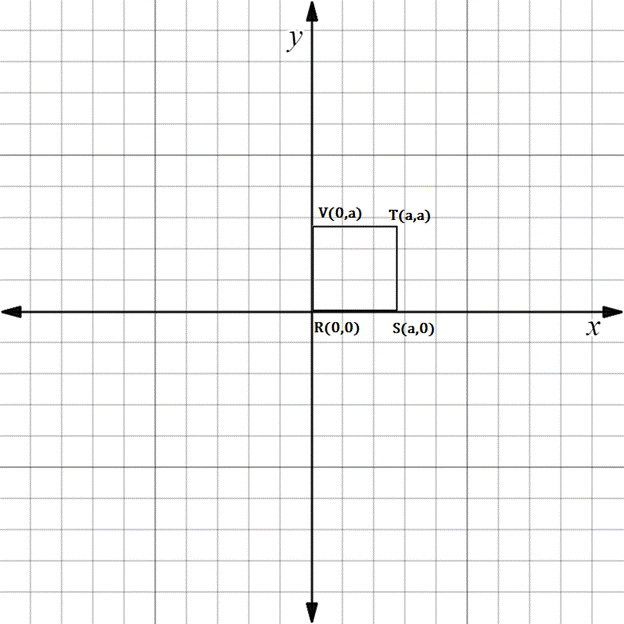
Chapter 10.3, Problem 10E
In Exercises 5 to 10, the real numbers a, b, c, and d are positive.
Consider the quadrilateral with vertices at
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 10 Solutions
Elementary Geometry For College Students, 7e
Ch. 10.1 - Plot and then label the points A0,-3, B3,-4, C5,...Ch. 10.1 - Give the coordinates of each point A, B, C, D, and...Ch. 10.1 - Find the distance between each pair of points: a...Ch. 10.1 - If the distance between -2, 3 and -2,a is 5 units,...Ch. 10.1 - If the distance between b,3 and 7, 3 is 3.5 units,...Ch. 10.1 - Prob. 6ECh. 10.1 - Find the distance between each pair of points: a...Ch. 10.1 - Find the distance between each pair of points: a...Ch. 10.1 - Find the midpoint of the line segment that joins...Ch. 10.1 - Prob. 10E
Ch. 10.1 - Points A and B have symmetry with respect to the...Ch. 10.1 - Points A and B have symmetry with respect to point...Ch. 10.1 - Points A and B have symmetry with respect to point...Ch. 10.1 - Points A and B have symmetry with respect to the...Ch. 10.1 - Prob. 15ECh. 10.1 - Points A and B have symmetry with respect to the...Ch. 10.1 - Points A and B have symmetry with respect to the...Ch. 10.1 - Prob. 18ECh. 10.1 - Points A and B have symmetry with respect to a...Ch. 10.1 - In Exercises 20 to 22, apply the Midpoint Formula....Ch. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - A rectangle ABCD has three of its vertices at...Ch. 10.1 - A rectangle MNPQ has three of its vertices at M0,...Ch. 10.1 - Use the Distance Formula to determine the type of...Ch. 10.1 - Use the method of Example 4 to find the equation...Ch. 10.1 - Use the method of Example 4 to find the equation...Ch. 10.1 - For coplanar points A,B, and C, suppose that you...Ch. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - There are two points on the x-axis that are...Ch. 10.1 - The triangle that has vertices at...Ch. 10.1 - Use the boxing method as suggested in Exercise 33,...Ch. 10.1 - Determine the area of ABC if A=2,1,B=5,3,andC is...Ch. 10.1 - Find the area of ABC In Exercise 35, but assume...Ch. 10.1 - Find the exact volume of the solid that results...Ch. 10.1 - Find the exact volume of the solid that results...Ch. 10.1 - Find the exact volume of the solid that results...Ch. 10.1 - Find the exact volume of the solid that results...Ch. 10.1 - Find the exact lateral area of each solid in...Ch. 10.1 - Find the volume of the solid formed when the...Ch. 10.1 - By definition, an ellipse is the locus of points...Ch. 10.1 - By definition, a hyperbola is the locus of points...Ch. 10.1 - Prob. 45ECh. 10.1 - Use the Distance Formula to show that the equation...Ch. 10.1 - Following a 90 counterclockwise rotation about the...Ch. 10.1 - Consider the point Ca,b. What is the image of C...Ch. 10.1 - Prob. 49ECh. 10.1 - The graphs of the parabolas eith equations y=x2...Ch. 10.1 - Prob. 51ECh. 10.2 - In Exercises 1 to 8, draw the graph of each...Ch. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - In Exercises 1 to 8, draw the graph of each...Ch. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Which points lie on the graph of 5x-4y=32? a 4,-3...Ch. 10.2 - Prob. 10ECh. 10.2 - Find the slopes of the lines containing: a 2,-3...Ch. 10.2 - Prob. 12ECh. 10.2 - Find x so that AB- has slope m, where: a A is...Ch. 10.2 - Prob. 14ECh. 10.2 - Are these points collinear? a A-2,5, B0,2, and...Ch. 10.2 - Are these points collinear? a A-1,-2, B3,2, and...Ch. 10.2 - Parallel lines l1 and l2 have slopes m1 and m2,...Ch. 10.2 - Prob. 18ECh. 10.2 - Perpendicular lines l1 and l2 have slopes m1 and...Ch. 10.2 - Prob. 20ECh. 10.2 - In Exercises 21 to 24, state whether the lines are...Ch. 10.2 - In Exercises 21 to 24, state whether the lines are...Ch. 10.2 - In Exercises 21 to 24, state whether the lines are...Ch. 10.2 - In Exercises 21 to 24, state whether the lines are...Ch. 10.2 - Find x such that the points Ax,5, B2,3, and C4,-5...Ch. 10.2 - Find a such that the points A1,3, B4,5, and Ca,a...Ch. 10.2 - Find x such that the line through 2,-3 and 3,2 is...Ch. 10.2 - Find x such that the line through 2,-3 and 3,2 is...Ch. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - In Exercises 29 to 34, draw the line described....Ch. 10.2 - In Exercises 29 to 34, draw the line described....Ch. 10.2 - In Exercises 29 to 34, draw the line described....Ch. 10.2 - Use slopes to decide whether the triangle with...Ch. 10.2 - If A2,2, B7,3, and C4,x are the vertices of a...Ch. 10.2 - If 2,3, 5,-2, and 7,2 are three vertices not...Ch. 10.2 - Three vertices of rectangle ABCD are A-5,1,...Ch. 10.2 - Show that quadrilateral RSTV is an isosceles...Ch. 10.2 - Show that quadrilateral ABCD is a parallelogram.Ch. 10.2 - Quadrilateral EFGH has the vertices E0,0, Fa,0,...Ch. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prove that if two lines neither horizontal nor...Ch. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Pentagon ABCDE has vertices A0,0, B0,b, Cd,c,...Ch. 10.3 - Find an expression for a The distance between a,0...Ch. 10.3 - Find the coordinates of the midpoint of the...Ch. 10.3 - Find the slope of the line containing the points a...Ch. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - In Exercises 5 to 10, the real numbers a, b, c,...Ch. 10.3 - Prob. 9ECh. 10.3 - In Exercises 5 to 10, the real numbers a, b, c,...Ch. 10.3 - In Exercises 11 to 16, supply the missing...Ch. 10.3 - In Exercises 11 to 16, supply the missing...Ch. 10.3 - In Exercises 11 to 16, supply the missing...Ch. 10.3 - Prob. 14ECh. 10.3 - In Exercises 11 to 16, supply the missing...Ch. 10.3 - In Exercises 11 to 16, supply the missing...Ch. 10.3 - In Exercises 17 to 22, draw an ideally placed...Ch. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - In Exercises 17 to 22, draw an ideally placed...Ch. 10.3 - In Exercises 17 to 22, draw an ideally placed...Ch. 10.3 - Prob. 22ECh. 10.3 - In Exercises 23 to 28, find the equation...Ch. 10.3 - In Exercises 23 to 28, find the equation...Ch. 10.3 - In Exercises 23 to 28, find the equation...Ch. 10.3 - In Exercises 23 to 28, find the equation...Ch. 10.3 - In Exercises 23 to 28, find the equation...Ch. 10.3 - Prob. 28ECh. 10.3 - The drawing shows isosceles ABC with AC-BC-. a...Ch. 10.3 - The drawing shows parallelogram RSTV. a What type...Ch. 10.3 - Prob. 31ECh. 10.3 - Which formula would you use to establish each of...Ch. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - In Exercises 33 to 36, draw and label a...Ch. 10.3 - In Exercises 33 to 36, draw and label a...Ch. 10.3 - ABCD is a rectangle with vertex A=a,b in Quadrant...Ch. 10.3 - Circle O has its center at the origin and contains...Ch. 10.3 - In RST, SV- bisects RST. Find the coordinates of...Ch. 10.3 - The graph of the parabola y=x2 contains the point...Ch. 10.3 - Prob. 41ECh. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - Prob. 6ECh. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - In Exercises 1 to 17, complete an analytic proof...Ch. 10.4 - Prob. 18ECh. 10.4 - Use the analytic method to decide what type of...Ch. 10.4 - Use slopes to verify that the graphs of the...Ch. 10.4 - Prob. 21ECh. 10.4 - Use the result in Exercise 20 to find the equation...Ch. 10.4 - Use the result in Exercise 20 to find the equation...Ch. 10.4 - Prob. 24ECh. 10.4 - Prob. 25ECh. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Based on the result in Exercise 26, describe the...Ch. 10.4 - Based on the result in Exercise 26, describe the...Ch. 10.4 - Suppose that the circle with center 0, 0 and...Ch. 10.4 - Prob. 32ECh. 10.4 - Prob. 33ECh. 10.4 - Complete an analytic proof of the following...Ch. 10.4 - Prob. 35ECh. 10.5 - In Exercises 1 to 4, use division to write an...Ch. 10.5 - Prob. 2ECh. 10.5 - In Exercises 1 to 4, use division to write an...Ch. 10.5 - Prob. 4ECh. 10.5 - Prob. 5ECh. 10.5 - Prob. 6ECh. 10.5 - Prob. 7ECh. 10.5 - Prob. 8ECh. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - Prob. 11ECh. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - Prob. 21ECh. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - In Exercises 9 to 24, find an equation of the line...Ch. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - In Exercises 27 to 32, use graphing to find the...Ch. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - In Exercises 27 to 32, use graphing to find the...Ch. 10.5 - Prob. 32ECh. 10.5 - In Exercises 33 to 38, use algebra to find the...Ch. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - In Exercises 33 to 38, use algebra to find the...Ch. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - In Exercises 39 to 42, use substitution to solve...Ch. 10.5 - Prob. 43ECh. 10.5 - For isosceles PNQ, the vertices are P-2a,0, N2a,0,...Ch. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - The y-axis along with the graphs of y=-2x+7 and...Ch. 10.6 - In the Cartesian coordinate system below, name the...Ch. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Find a direction vector for the line containing...Ch. 10.6 - For the line l:x,y,z=2,3,4+n3,-2,5, find a a point...Ch. 10.6 - For the line l:x,y,z=5,3,-2+n1,2,-2, find a a...Ch. 10.6 - Prob. 7ECh. 10.6 - In vector form as in Exercises 5 and 6, find an...Ch. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - In Exercises 11 to 14, find the distance between...Ch. 10.6 - In Exercises 11 to 14, find the distance between...Ch. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - In Exercises 15 to 18, find the midpoint of the...Ch. 10.6 - Prob. 17ECh. 10.6 - In Exercises 15 to 18, find the midpoint of the...Ch. 10.6 - In Exercises 19 and 20, use the x, y, and...Ch. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - In Exercises 23 to 26, find an equation for each...Ch. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - The line x,y,z=3,4,5+n3,4,-5 intersects the sphere...Ch. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - For the sphers x-12+y+22+z-42=36 and x2+y2+z2=64,...Ch. 10.6 - Does the sphere x2+y2+z2=100 have symmetry with...Ch. 10.6 - Prob. 43ECh. 10.6 - Lines l1: x,y,z=2,0,3+n2,-3,5 and l2:...Ch. 10.6 - The planes with the equation x+2z=12 and y-3z=6...Ch. 10.6 - Prob. 46ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.CR - Find the distance between each pair of points: a...Ch. 10.CR - Prob. 2CRCh. 10.CR - Find the midpoint of the line segment that joins...Ch. 10.CR - Prob. 4CRCh. 10.CR - Find the slope of the line containing each pair of...Ch. 10.CR - Find the slope of the line containing each pair of...Ch. 10.CR - 2,1 is the midpoint of AB-, in which A has...Ch. 10.CR - Prob. 8CRCh. 10.CR - If A has coordinates 2,1 and B has coordinates...Ch. 10.CR - Prob. 10CRCh. 10.CR - Without graphing, determine whether the pair of...Ch. 10.CR - Determine whether the points -6,5, 1,7, and 16,10...Ch. 10.CR - Prob. 13CRCh. 10.CR - Draw the graph of 3x+7y=21, and name the...Ch. 10.CR - Prob. 15CRCh. 10.CR - Prob. 16CRCh. 10.CR - Write an equation for a the line through 2,3 and...Ch. 10.CR - Prob. 18CRCh. 10.CR - Show that the triangle whose vertices are A3,6,...Ch. 10.CR - Prob. 20CRCh. 10.CR - Prob. 21CRCh. 10.CR - Prob. 22CRCh. 10.CR - In Review Exercises 23 and 24, solve the system of...Ch. 10.CR - Prob. 24CRCh. 10.CR - Three of the four vertices of a parallelogram are...Ch. 10.CR - A3,1, B5,9, and C11,3 are the vertices of ABC. a...Ch. 10.CR - Prob. 27CRCh. 10.CR - Prob. 28CRCh. 10.CR - In Review Exercise 27 to 30, supply the missing...Ch. 10.CR - In Review Exercise 27 to 30, supply the missing...Ch. 10.CR - A2a,2b, B2c,2d, and C0,2e are the vertices of ABC....Ch. 10.CR - Prove the statements in Review Exercises 32 to 36...Ch. 10.CR - Prove the statements in Review Exercises 32 to 36...Ch. 10.CR - Prove the statements in Review Exercises 32 to 36...Ch. 10.CR - Prove the statements in Review Exercises 32 to 36...Ch. 10.CR - Prove the statements in Review Exercises 32 to 36...Ch. 10.CR - Determine whether ABC, with vertices A0,0,0,...Ch. 10.CR - Prob. 38CRCh. 10.CR - Prob. 39CRCh. 10.CR - Prob. 40CRCh. 10.CT - In the coordinate system provided, give the...Ch. 10.CT - Prob. 2CTCh. 10.CT - Prob. 3CTCh. 10.CT - Prob. 4CTCh. 10.CT - Complete the following table of x and...Ch. 10.CT - Using the table from Exercise 5, sketch the graph...Ch. 10.CT - Prob. 7CTCh. 10.CT - Prob. 8CTCh. 10.CT - Prob. 9CTCh. 10.CT - Prob. 10CTCh. 10.CT - Prob. 11CTCh. 10.CT - Prob. 12CTCh. 10.CT - Using as few variables as possible, state the...Ch. 10.CT - Prob. 14CTCh. 10.CT - Prob. 15CTCh. 10.CT - Prob. 16CTCh. 10.CT - Prob. 17CTCh. 10.CT - Prob. 18CTCh. 10.CT - Prob. 19CTCh. 10.CT - Prob. 20CTCh. 10.CT - Prob. 21CTCh. 10.CT - Prob. 22CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- In Exercises 5 to 10, the real numbers a, b, c, and d are positive. Consider the quadrilateral with vertices at A0,0, Ba,0, Cb,c, and Dd,c. Explain why ABCD is a trapezoid.arrow_forwardIn Exercises 29 to 31, M and Nare the midpoints of sides RS and RT ofRST, respectively. Given: MN=x2+5 ST=x2x+5 Find: x, MN, STarrow_forwardIn Exercises15 to 19, create drawing as needed. Given: Square ABCD with diagonals DB and AC intersecting at E DC=53 Find: DBarrow_forward
- In Exercises 19 to 24, complete each proof. Given: Quadrilateral ABCD, with midpoints E, F, G, and H of the sides Prove: EFHG PROOF Statements Reasons 1. ? 1. Given 2. Draw AC 2. Through two points, there is one line 3. In ABC, EFAC and in ADC, HGAC 3. ? 4. ? 4. If two lines are to the same line, these lines are to each otherarrow_forwardIn Exercises 39 to 47, provide a paragraph proof. Be sure to provide a drawing, Given, and Prove where needed. If a parallelogram is inscribed in a circle, then it is a rectangle.arrow_forwardIn Exercises 7 and 8, classify the trianglenot shown by considering the lengths of its sides. a In XYZ, XYYZ. b In RST, RS=6, ST=7, and RT=8.arrow_forward
- In Exercises 11 to 18, state the hypothesis and the conclusion of each statement. If the diagonals of a parallelogram are perpendicular, then the parallelogram is a rhombus.arrow_forwardIn Exercises 1 to 6, l and m are cut by transversal v. On the basis of the information given, determine whether l must be parallel to m. m1 = 107 and m5 = 107arrow_forwardIn Exercises 29 to 31, M and Nare the midpoints of sides RS and RT ofRST, respectively. Given: RM=RN=2x+1 ST=5x-3 mR=60 Find: x, RM, and STarrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY