
Calculus
10th Edition
ISBN: 9781285057095
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Question
Chapter 10.3, Problem 94E
To determine
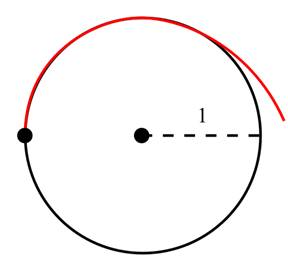
To calculate: The area is covered when string is unwound counters clockwise as given in the figure below:
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 10 Solutions
Calculus
Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Sketching a Parabola In Exercises 1116, find the...
Ch. 10.1 - Sketching a Parabola In Exercises 1116, find the...Ch. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Finding the Standard Equation of an Ellipse In...Ch. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 57ECh. 10.1 - Classifying the Graph of an Equation In Exercises...Ch. 10.1 - Prob. 55ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 63ECh. 10.1 - Prob. 69ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Prob. 61ECh. 10.1 - Eccentricity Define the eccentricity of an...Ch. 10.1 - Prob. 64ECh. 10.1 - Solar Collector A solar collector for heating...Ch. 10.1 - Beam Deflection A simply supported beam that is 16...Ch. 10.1 - Prob. 67ECh. 10.1 - Proof (a) Prove that if any two tangent lines to a...Ch. 10.1 - Bridge Design A cable of a suspension bridge is...Ch. 10.1 - Prob. 71ECh. 10.1 - Surface Area A satellite signal receiving dish is...Ch. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.1 - Prob. 75ECh. 10.1 - Prob. 76ECh. 10.1 - Prob. 77ECh. 10.1 - Prob. 78ECh. 10.1 - Prob. 79ECh. 10.1 - Prob. 80ECh. 10.1 - Prob. 81ECh. 10.1 - Conjecture Show that the equation of an ellipse...Ch. 10.1 - Prob. 83ECh. 10.1 - Prob. 84ECh. 10.1 - Prob. 85ECh. 10.1 - Prob. 86ECh. 10.1 - Prob. 87ECh. 10.1 - Hyperbolic Mirror A hyperbolic mirror (used in...Ch. 10.1 - Prob. 89ECh. 10.1 - Prob. 90ECh. 10.1 - True or False? In Exercises 8792, determine...Ch. 10.1 - Prob. 92ECh. 10.1 - Prob. 93ECh. 10.1 - True or False? In Exercises 87-92, determine...Ch. 10.1 - True or False? In Exercises 8792, determine...Ch. 10.1 - Prob. 96ECh. 10.1 - For a point P on an ellipse, let d be the distance...Ch. 10.1 - Prob. 98ECh. 10.2 - Prob. 1ECh. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 26ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - Prob. 49ECh. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Prob. 53ECh. 10.2 - Prob. 54ECh. 10.2 - Prob. 55ECh. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - Prob. 61ECh. 10.2 - Prob. 62ECh. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Plane Curve Explain the process of sketching a...Ch. 10.2 - Prob. 67ECh. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - Epicycloid A circle of radius 1 rolls around the...Ch. 10.2 - Prob. 75ECh. 10.2 - Prob. 76ECh. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - Projectile Motion In Exercises 81 and 82, consider...Ch. 10.2 - Projectile Motion In Exercises 81 and 82, consider...Ch. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Horizontal and Vertical Tangency In Exercises 27...Ch. 10.3 - Horizontal and Vertical Tangency In Exercises 31...Ch. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Prob. 53ECh. 10.3 - Arc Length In Exercises 5154, find the are length...Ch. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 66ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 68ECh. 10.3 - Prob. 69ECh. 10.3 - Prob. 70ECh. 10.3 - Prob. 61ECh. 10.3 - Surface Area In Exercises 6164, write an integral...Ch. 10.3 - Prob. 63ECh. 10.3 - Prob. 64ECh. 10.3 - Prob. 71ECh. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Prob. 77ECh. 10.3 - Prob. 78ECh. 10.3 - Area In Exercises 79 and 80, find the area of the...Ch. 10.3 - Prob. 80ECh. 10.3 - Prob. 81ECh. 10.3 - Prob. 82ECh. 10.3 - Prob. 83ECh. 10.3 - Prob. 84ECh. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Prob. 86ECh. 10.3 - Prob. 87ECh. 10.3 - Prob. 88ECh. 10.3 - Prob. 89ECh. 10.3 - Volume In Exercises 89 and 90, find the volume of...Ch. 10.3 - Prob. 91ECh. 10.3 - Prob. 92ECh. 10.3 - Prob. 93ECh. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - Prob. 96ECh. 10.3 - True or False? In Exercises 97-100, determine...Ch. 10.3 - Prob. 98ECh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Rectangular-to Polar Conversion In Exercises 2534,...Ch. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 96ECh. 10.4 - Prob. 97ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Prob. 60ECh. 10.4 - Prob. 59ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.4 - Prob. 67ECh. 10.4 - Prob. 68ECh. 10.4 - Prob. 69ECh. 10.4 - Prob. 70ECh. 10.4 - Prob. 71ECh. 10.4 - Prob. 72ECh. 10.4 - Prob. 73ECh. 10.4 - Prob. 74ECh. 10.4 - Prob. 75ECh. 10.4 - Prob. 76ECh. 10.4 - Prob. 77ECh. 10.4 - Prob. 78ECh. 10.4 - Prob. 79ECh. 10.4 - Prob. 80ECh. 10.4 - Prob. 81ECh. 10.4 - Prob. 82ECh. 10.4 - Prob. 83ECh. 10.4 - Prob. 84ECh. 10.4 - Prob. 85ECh. 10.4 - Prob. 86ECh. 10.4 - Prob. 87ECh. 10.4 - Prob. 88ECh. 10.4 - Prob. 89ECh. 10.4 - Prob. 90ECh. 10.4 - Prob. 91ECh. 10.4 - Prob. 92ECh. 10.4 - Prob. 93ECh. 10.4 - Prob. 94ECh. 10.4 - Prob. 95ECh. 10.4 - Prob. 98ECh. 10.4 - Prob. 99ECh. 10.4 - Prob. 100ECh. 10.4 - Rotated Curve In Exercises 101104, use the results...Ch. 10.4 - Rotated Curve In Exercises 103-105, use the...Ch. 10.4 - Prob. 103ECh. 10.4 - Proof Prove that the tangent of the angle (0/2)...Ch. 10.4 - Prob. 105ECh. 10.4 - Prob. 106ECh. 10.4 - Prob. 107ECh. 10.4 - Prob. 108ECh. 10.4 - Prob. 109ECh. 10.4 - Prob. 110ECh. 10.4 - Prob. 111ECh. 10.4 - Prob. 112ECh. 10.4 - Prob. 113ECh. 10.4 - Prob. 114ECh. 10.5 - Points of Intersection Explain why finding points...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 6ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Prob. 63ECh. 10.5 - Prob. 64ECh. 10.5 - Prob. 65ECh. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 70ECh. 10.5 - 57095-10.5-71E-Question-Digital.docx WRITING ABOUT...Ch. 10.5 - Prob. 72ECh. 10.5 - Surface Area of a Torus Find the surface area of...Ch. 10.5 - Surface Area of a Tours Find the surface area of...Ch. 10.5 - Prob. 75ECh. 10.5 - Prob. 76ECh. 10.5 - Prob. 77ECh. 10.5 - Prob. 78ECh. 10.5 - Prob. 79ECh. 10.5 - Logarithmic Spiral The curve represented by the...Ch. 10.5 - Prob. 81ECh. 10.5 - Prob. 82ECh. 10.5 - Prob. 83ECh. 10.5 - Prob. 84ECh. 10.5 - Prob. 85ECh. 10.6 - Prob. 1ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Area of a Region In Exercises 55-58, use the...Ch. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - Prob. 61ECh. 10.6 - Prob. 62ECh. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.6 - Comet Hale-Bopp The comet Hale-Bopp has an...Ch. 10.6 - Eccentricity In Exercises 67 and 68, let r0...Ch. 10.6 - Prob. 70ECh. 10 - Matching In Exercises 1-6, match the equation with...Ch. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - 26. Using an Ellipse Consider the ellipse .
...Ch. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - 57095-10-47RE-Question-Digital.docx Finding an...Ch. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 113RECh. 10 - Prob. 114RECh. 10 - Prob. 115RECh. 10 - Prob. 116RECh. 10 - Prob. 117RECh. 10 - Prob. 118RECh. 10 - Prob. 119RECh. 10 - Prob. 120RECh. 10 - Prob. 121RECh. 10 - Prob. 122RECh. 10 - Prob. 123RECh. 10 - Prob. 124RECh. 10 - Prob. 1PSCh. 10 - Prob. 2PSCh. 10 - Prob. 3PSCh. 10 - Flight Paths An air traffic controller spots two...Ch. 10 - Prob. 5PSCh. 10 - Prob. 6PSCh. 10 - Cornu Spiral Consider the cornu spiral given by...Ch. 10 - Prob. 8PSCh. 10 - Prob. 9PSCh. 10 - Prob. 10PSCh. 10 - Prob. 11PSCh. 10 - Prob. 12PSCh. 10 - Prob. 13PSCh. 10 - Prob. 14PSCh. 10 - Prob. 15PSCh. 10 - Prob. 16PSCh. 10 - Prob. 17PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Area of a Tabletop Yuki bought a drop-leaf kitchen table. The rectangular part of the table is a 1-ft by 3-ft rectangle with a semicircle at each end. as shown. (a) Find the area of the table with one leaf up. (b) Find the area of the table with both leaves up.arrow_forwardA cross section of an aluminum bar in the shape of a trapezoid is shown. All the dimensions are in inches. a. Find the cross-sectional area of the bar. b. Find the length of side AB. Round the answer to the nearest hundredth inch.arrow_forwardDimensions of a Garden A gardener has 100 meters of fencing to enclose two adjacent rectangular gardens (see figure). The gardener wants the enclosed area to be 350 square meters. What dimensions should the gardener use to obtain this area ?arrow_forward
- Girth of a Box A box with a square base has length plus girth or 108 in. (Girth is the distance "around" the box.) What is the length of the box if its volume is 2200 in3?arrow_forwardA landscaper wants to put a square reflecting pool next to a triangular deck, as shown below. The triangular deck is a right triangle, with legs of length 9 feet and 11 feet, and the pool will be adjacent to the hypotenuse. (a) Use the Pythagorean Theorem to find the length of a side of the pool. Round your answer to the nearest tenth of a foot. (b) Find the exact area of the pool.arrow_forwardHeight of a Tree You measure a tree’s shadow and find that it is 8 meters long. Then you measure the shadow of a nearby two-meter lamppost and find that it is 75 centimeters long. (See figure.) How tall is the tree?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

College Algebra
Algebra
ISBN:9781305115545
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Problems on Area and Circumference of Circle| Basics of Circle| Questions on Circle||BrainPanthers; Author: Brain Panthers;https://www.youtube.com/watch?v=RcNEL9OzcC0;License: Standard YouTube License, CC-BY