
Calculus
10th Edition
ISBN: 9781285057095
Author: Ron Larson, Bruce H. Edwards
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10.5, Problem 2E
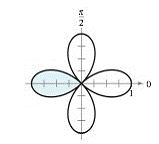
Area of a Polar Region In Exercises 3-6, write an
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
How do you find the area of a region 0 ≤ r1(θ) ≤ r ≤ r2(θ),a≤ θ ≤ b, in the polar coordinate plane? Give examples.
area-polar-1
Determine the area of the right half of the cardioid formed by
r = 9 + 8 sinθ
Area of cardioid right half is:
Calculus math/ Area in polar coordinates
Chapter 10 Solutions
Calculus
Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Matching In Exercises 5-10, match the equation...Ch. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Sketching a Parabola In Exercises 1116, find the...
Ch. 10.1 - Sketching a Parabola In Exercises 1116, find the...Ch. 10.1 - Prob. 12ECh. 10.1 - Prob. 13ECh. 10.1 - Prob. 14ECh. 10.1 - Prob. 15ECh. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - Prob. 18ECh. 10.1 - Prob. 19ECh. 10.1 - Prob. 20ECh. 10.1 - Prob. 21ECh. 10.1 - Prob. 22ECh. 10.1 - Prob. 23ECh. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Prob. 28ECh. 10.1 - Prob. 29ECh. 10.1 - Prob. 30ECh. 10.1 - Prob. 31ECh. 10.1 - Prob. 32ECh. 10.1 - Prob. 33ECh. 10.1 - Finding the Standard Equation of an Ellipse In...Ch. 10.1 - Prob. 35ECh. 10.1 - Prob. 36ECh. 10.1 - Prob. 37ECh. 10.1 - Prob. 38ECh. 10.1 - Prob. 39ECh. 10.1 - Prob. 40ECh. 10.1 - Prob. 41ECh. 10.1 - Prob. 42ECh. 10.1 - Prob. 43ECh. 10.1 - Prob. 44ECh. 10.1 - Prob. 45ECh. 10.1 - Prob. 46ECh. 10.1 - Prob. 47ECh. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Prob. 50ECh. 10.1 - Prob. 53ECh. 10.1 - Prob. 51ECh. 10.1 - Prob. 52ECh. 10.1 - Prob. 57ECh. 10.1 - Classifying the Graph of an Equation In Exercises...Ch. 10.1 - Prob. 55ECh. 10.1 - Prob. 54ECh. 10.1 - Prob. 63ECh. 10.1 - Prob. 69ECh. 10.1 - Prob. 56ECh. 10.1 - Prob. 59ECh. 10.1 - Prob. 60ECh. 10.1 - Prob. 61ECh. 10.1 - Eccentricity Define the eccentricity of an...Ch. 10.1 - Prob. 64ECh. 10.1 - Solar Collector A solar collector for heating...Ch. 10.1 - Beam Deflection A simply supported beam that is 16...Ch. 10.1 - Prob. 67ECh. 10.1 - Proof (a) Prove that if any two tangent lines to a...Ch. 10.1 - Bridge Design A cable of a suspension bridge is...Ch. 10.1 - Prob. 71ECh. 10.1 - Surface Area A satellite signal receiving dish is...Ch. 10.1 - Prob. 73ECh. 10.1 - Prob. 74ECh. 10.1 - Prob. 75ECh. 10.1 - Prob. 76ECh. 10.1 - Prob. 77ECh. 10.1 - Prob. 78ECh. 10.1 - Prob. 79ECh. 10.1 - Prob. 80ECh. 10.1 - Prob. 81ECh. 10.1 - Conjecture Show that the equation of an ellipse...Ch. 10.1 - Prob. 83ECh. 10.1 - Prob. 84ECh. 10.1 - Prob. 85ECh. 10.1 - Prob. 86ECh. 10.1 - Prob. 87ECh. 10.1 - Hyperbolic Mirror A hyperbolic mirror (used in...Ch. 10.1 - Prob. 89ECh. 10.1 - Prob. 90ECh. 10.1 - True or False? In Exercises 8792, determine...Ch. 10.1 - Prob. 92ECh. 10.1 - Prob. 93ECh. 10.1 - True or False? In Exercises 87-92, determine...Ch. 10.1 - True or False? In Exercises 8792, determine...Ch. 10.1 - Prob. 96ECh. 10.1 - For a point P on an ellipse, let d be the distance...Ch. 10.1 - Prob. 98ECh. 10.2 - Prob. 1ECh. 10.2 - Prob. 2ECh. 10.2 - Prob. 3ECh. 10.2 - Prob. 4ECh. 10.2 - Prob. 5ECh. 10.2 - Prob. 6ECh. 10.2 - Prob. 7ECh. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Prob. 12ECh. 10.2 - Prob. 13ECh. 10.2 - Prob. 14ECh. 10.2 - Prob. 15ECh. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 5-22,...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 21ECh. 10.2 - Prob. 22ECh. 10.2 - Prob. 23ECh. 10.2 - Prob. 24ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 26ECh. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Using Parametric Equations In Exercises 23-34, use...Ch. 10.2 - Prob. 29ECh. 10.2 - Prob. 30ECh. 10.2 - Prob. 31ECh. 10.2 - Prob. 32ECh. 10.2 - Prob. 33ECh. 10.2 - Prob. 34ECh. 10.2 - Prob. 35ECh. 10.2 - Prob. 36ECh. 10.2 - Prob. 37ECh. 10.2 - Prob. 38ECh. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Writing a Set of Parametric Equations In Exercises...Ch. 10.2 - Prob. 42ECh. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Prob. 48ECh. 10.2 - Prob. 49ECh. 10.2 - Prob. 50ECh. 10.2 - Prob. 51ECh. 10.2 - Prob. 52ECh. 10.2 - Prob. 53ECh. 10.2 - Prob. 54ECh. 10.2 - Prob. 55ECh. 10.2 - Prob. 56ECh. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - Prob. 61ECh. 10.2 - Prob. 62ECh. 10.2 - Prob. 63ECh. 10.2 - Prob. 64ECh. 10.2 - Prob. 65ECh. 10.2 - Plane Curve Explain the process of sketching a...Ch. 10.2 - Prob. 67ECh. 10.2 - Prob. 68ECh. 10.2 - Prob. 69ECh. 10.2 - Prob. 70ECh. 10.2 - Prob. 71ECh. 10.2 - Prob. 72ECh. 10.2 - Prob. 73ECh. 10.2 - Epicycloid A circle of radius 1 rolls around the...Ch. 10.2 - Prob. 75ECh. 10.2 - Prob. 76ECh. 10.2 - Prob. 77ECh. 10.2 - Prob. 78ECh. 10.2 - Projectile Motion In Exercises 81 and 82, consider...Ch. 10.2 - Projectile Motion In Exercises 81 and 82, consider...Ch. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Prob. 3ECh. 10.3 - Prob. 4ECh. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Prob. 7ECh. 10.3 - Prob. 8ECh. 10.3 - Prob. 9ECh. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Prob. 15ECh. 10.3 - Prob. 16ECh. 10.3 - Prob. 17ECh. 10.3 - Prob. 18ECh. 10.3 - Prob. 19ECh. 10.3 - Prob. 20ECh. 10.3 - Finding an Equation of a Tangent Line In Exercises...Ch. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Finding Equations of Tangent Lines In Exercises...Ch. 10.3 - Prob. 25ECh. 10.3 - Prob. 26ECh. 10.3 - Horizontal and Vertical Tangency In Exercises 27...Ch. 10.3 - Horizontal and Vertical Tangency In Exercises 31...Ch. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 32ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 33ECh. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 37ECh. 10.3 - Prob. 36ECh. 10.3 - Prob. 38ECh. 10.3 - Prob. 39ECh. 10.3 - Prob. 40ECh. 10.3 - Prob. 41ECh. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 49-54, find the arc length...Ch. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Arc Length In Exercises 55-58, find the arc length...Ch. 10.3 - Prob. 53ECh. 10.3 - Arc Length In Exercises 5154, find the are length...Ch. 10.3 - Prob. 55ECh. 10.3 - Prob. 56ECh. 10.3 - Prob. 57ECh. 10.3 - Prob. 58ECh. 10.3 - Prob. 59ECh. 10.3 - Prob. 60ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 66ECh. 10.3 - Surface Area In Exercises 63-68, find the area of...Ch. 10.3 - Prob. 68ECh. 10.3 - Prob. 69ECh. 10.3 - Prob. 70ECh. 10.3 - Prob. 61ECh. 10.3 - Surface Area In Exercises 6164, write an integral...Ch. 10.3 - Prob. 63ECh. 10.3 - Prob. 64ECh. 10.3 - Prob. 71ECh. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - Prob. 74ECh. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Prob. 77ECh. 10.3 - Prob. 78ECh. 10.3 - Area In Exercises 79 and 80, find the area of the...Ch. 10.3 - Prob. 80ECh. 10.3 - Prob. 81ECh. 10.3 - Prob. 82ECh. 10.3 - Prob. 83ECh. 10.3 - Prob. 84ECh. 10.3 - Areas of Simple Closed Curves In Exercises 81-86,...Ch. 10.3 - Prob. 86ECh. 10.3 - Prob. 87ECh. 10.3 - Prob. 88ECh. 10.3 - Prob. 89ECh. 10.3 - Volume In Exercises 89 and 90, find the volume of...Ch. 10.3 - Prob. 91ECh. 10.3 - Prob. 92ECh. 10.3 - Prob. 93ECh. 10.3 - Prob. 94ECh. 10.3 - Prob. 95ECh. 10.3 - Prob. 96ECh. 10.3 - True or False? In Exercises 97-100, determine...Ch. 10.3 - Prob. 98ECh. 10.4 - Prob. 1ECh. 10.4 - Prob. 2ECh. 10.4 - Prob. 3ECh. 10.4 - Prob. 4ECh. 10.4 - Prob. 5ECh. 10.4 - Prob. 6ECh. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Prob. 10ECh. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Prob. 15ECh. 10.4 - Prob. 16ECh. 10.4 - Prob. 17ECh. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Prob. 20ECh. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Rectangular-to Polar Conversion In Exercises 2534,...Ch. 10.4 - Prob. 26ECh. 10.4 - Prob. 27ECh. 10.4 - Prob. 28ECh. 10.4 - Prob. 29ECh. 10.4 - Prob. 30ECh. 10.4 - Prob. 31ECh. 10.4 - Rectangular-to-Polar Conversion In Exercises...Ch. 10.4 - Prob. 33ECh. 10.4 - Prob. 34ECh. 10.4 - Prob. 35ECh. 10.4 - Prob. 36ECh. 10.4 - Prob. 37ECh. 10.4 - Prob. 38ECh. 10.4 - Prob. 39ECh. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Polar-to-Rectangular Conversion In Exercises...Ch. 10.4 - Prob. 43ECh. 10.4 - Prob. 44ECh. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Prob. 47ECh. 10.4 - Prob. 48ECh. 10.4 - Prob. 49ECh. 10.4 - Prob. 50ECh. 10.4 - Prob. 51ECh. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 96ECh. 10.4 - Prob. 97ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.4 - Prob. 57ECh. 10.4 - Prob. 58ECh. 10.4 - Prob. 60ECh. 10.4 - Prob. 59ECh. 10.4 - Prob. 61ECh. 10.4 - Prob. 62ECh. 10.4 - Prob. 63ECh. 10.4 - Prob. 64ECh. 10.4 - Prob. 65ECh. 10.4 - Prob. 66ECh. 10.4 - Prob. 67ECh. 10.4 - Prob. 68ECh. 10.4 - Prob. 69ECh. 10.4 - Prob. 70ECh. 10.4 - Prob. 71ECh. 10.4 - Prob. 72ECh. 10.4 - Prob. 73ECh. 10.4 - Prob. 74ECh. 10.4 - Prob. 75ECh. 10.4 - Prob. 76ECh. 10.4 - Prob. 77ECh. 10.4 - Prob. 78ECh. 10.4 - Prob. 79ECh. 10.4 - Prob. 80ECh. 10.4 - Prob. 81ECh. 10.4 - Prob. 82ECh. 10.4 - Prob. 83ECh. 10.4 - Prob. 84ECh. 10.4 - Prob. 85ECh. 10.4 - Prob. 86ECh. 10.4 - Prob. 87ECh. 10.4 - Prob. 88ECh. 10.4 - Prob. 89ECh. 10.4 - Prob. 90ECh. 10.4 - Prob. 91ECh. 10.4 - Prob. 92ECh. 10.4 - Prob. 93ECh. 10.4 - Prob. 94ECh. 10.4 - Prob. 95ECh. 10.4 - Prob. 98ECh. 10.4 - Prob. 99ECh. 10.4 - Prob. 100ECh. 10.4 - Rotated Curve In Exercises 101104, use the results...Ch. 10.4 - Rotated Curve In Exercises 103-105, use the...Ch. 10.4 - Prob. 103ECh. 10.4 - Proof Prove that the tangent of the angle (0/2)...Ch. 10.4 - Prob. 105ECh. 10.4 - Prob. 106ECh. 10.4 - Prob. 107ECh. 10.4 - Prob. 108ECh. 10.4 - Prob. 109ECh. 10.4 - Prob. 110ECh. 10.4 - Prob. 111ECh. 10.4 - Prob. 112ECh. 10.4 - Prob. 113ECh. 10.4 - Prob. 114ECh. 10.5 - Points of Intersection Explain why finding points...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Area of a Polar Region In Exercises 3-6, write an...Ch. 10.5 - Prob. 3ECh. 10.5 - Prob. 4ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 6ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Finding the Area of a Polar Region In Exercises...Ch. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Prob. 14ECh. 10.5 - Prob. 15ECh. 10.5 - Prob. 16ECh. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Prob. 21ECh. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Finding Points of Intersection In Exercises 27-34,...Ch. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Finding the Area of a Polar Region Between Two...Ch. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - Prob. 50ECh. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Prob. 55ECh. 10.5 - Prob. 56ECh. 10.5 - Prob. 57ECh. 10.5 - Prob. 58ECh. 10.5 - Prob. 59ECh. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Prob. 63ECh. 10.5 - Prob. 64ECh. 10.5 - Prob. 65ECh. 10.5 - Prob. 66ECh. 10.5 - Prob. 67ECh. 10.5 - Prob. 68ECh. 10.5 - Prob. 70ECh. 10.5 - 57095-10.5-71E-Question-Digital.docx WRITING ABOUT...Ch. 10.5 - Prob. 72ECh. 10.5 - Surface Area of a Torus Find the surface area of...Ch. 10.5 - Surface Area of a Tours Find the surface area of...Ch. 10.5 - Prob. 75ECh. 10.5 - Prob. 76ECh. 10.5 - Prob. 77ECh. 10.5 - Prob. 78ECh. 10.5 - Prob. 79ECh. 10.5 - Logarithmic Spiral The curve represented by the...Ch. 10.5 - Prob. 81ECh. 10.5 - Prob. 82ECh. 10.5 - Prob. 83ECh. 10.5 - Prob. 84ECh. 10.5 - Prob. 85ECh. 10.6 - Prob. 1ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10.6 - Prob. 32ECh. 10.6 - Prob. 33ECh. 10.6 - Prob. 34ECh. 10.6 - Prob. 35ECh. 10.6 - Prob. 36ECh. 10.6 - Prob. 37ECh. 10.6 - Prob. 38ECh. 10.6 - Prob. 39ECh. 10.6 - Prob. 40ECh. 10.6 - Prob. 41ECh. 10.6 - Prob. 42ECh. 10.6 - Prob. 43ECh. 10.6 - Prob. 44ECh. 10.6 - Prob. 45ECh. 10.6 - Prob. 46ECh. 10.6 - Prob. 47ECh. 10.6 - Prob. 48ECh. 10.6 - Prob. 49ECh. 10.6 - Prob. 50ECh. 10.6 - Prob. 51ECh. 10.6 - Prob. 52ECh. 10.6 - Prob. 53ECh. 10.6 - Prob. 54ECh. 10.6 - Prob. 55ECh. 10.6 - Prob. 56ECh. 10.6 - Area of a Region In Exercises 55-58, use the...Ch. 10.6 - Prob. 58ECh. 10.6 - Prob. 59ECh. 10.6 - Prob. 60ECh. 10.6 - Prob. 61ECh. 10.6 - Prob. 62ECh. 10.6 - Prob. 63ECh. 10.6 - Prob. 64ECh. 10.6 - Prob. 65ECh. 10.6 - Prob. 66ECh. 10.6 - Prob. 67ECh. 10.6 - Comet Hale-Bopp The comet Hale-Bopp has an...Ch. 10.6 - Eccentricity In Exercises 67 and 68, let r0...Ch. 10.6 - Prob. 70ECh. 10 - Matching In Exercises 1-6, match the equation with...Ch. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Prob. 14RECh. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Prob. 21RECh. 10 - Prob. 22RECh. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - 26. Using an Ellipse Consider the ellipse .
...Ch. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Prob. 32RECh. 10 - Prob. 33RECh. 10 - Prob. 34RECh. 10 - Prob. 35RECh. 10 - Prob. 36RECh. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - 57095-10-47RE-Question-Digital.docx Finding an...Ch. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Prob. 51RECh. 10 - Prob. 52RECh. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - Prob. 57RECh. 10 - Prob. 58RECh. 10 - Prob. 59RECh. 10 - Prob. 60RECh. 10 - Prob. 61RECh. 10 - Prob. 62RECh. 10 - Prob. 63RECh. 10 - Prob. 64RECh. 10 - Prob. 65RECh. 10 - Prob. 66RECh. 10 - Prob. 67RECh. 10 - Prob. 68RECh. 10 - Prob. 69RECh. 10 - Prob. 70RECh. 10 - Prob. 71RECh. 10 - Prob. 72RECh. 10 - Prob. 73RECh. 10 - Prob. 74RECh. 10 - Prob. 75RECh. 10 - Prob. 76RECh. 10 - Prob. 77RECh. 10 - Prob. 78RECh. 10 - Prob. 79RECh. 10 - Prob. 80RECh. 10 - Prob. 81RECh. 10 - Prob. 82RECh. 10 - Prob. 83RECh. 10 - Prob. 84RECh. 10 - Prob. 85RECh. 10 - Prob. 86RECh. 10 - Prob. 87RECh. 10 - Prob. 88RECh. 10 - Prob. 89RECh. 10 - Prob. 90RECh. 10 - Prob. 91RECh. 10 - Prob. 92RECh. 10 - Prob. 93RECh. 10 - Prob. 94RECh. 10 - Prob. 95RECh. 10 - Prob. 96RECh. 10 - Prob. 97RECh. 10 - Prob. 98RECh. 10 - Prob. 99RECh. 10 - Prob. 100RECh. 10 - Prob. 101RECh. 10 - Prob. 102RECh. 10 - Prob. 107RECh. 10 - Prob. 108RECh. 10 - Prob. 103RECh. 10 - Prob. 104RECh. 10 - Prob. 105RECh. 10 - Prob. 106RECh. 10 - Prob. 109RECh. 10 - Prob. 110RECh. 10 - Prob. 111RECh. 10 - Prob. 112RECh. 10 - Prob. 113RECh. 10 - Prob. 114RECh. 10 - Prob. 115RECh. 10 - Prob. 116RECh. 10 - Prob. 117RECh. 10 - Prob. 118RECh. 10 - Prob. 119RECh. 10 - Prob. 120RECh. 10 - Prob. 121RECh. 10 - Prob. 122RECh. 10 - Prob. 123RECh. 10 - Prob. 124RECh. 10 - Prob. 1PSCh. 10 - Prob. 2PSCh. 10 - Prob. 3PSCh. 10 - Flight Paths An air traffic controller spots two...Ch. 10 - Prob. 5PSCh. 10 - Prob. 6PSCh. 10 - Cornu Spiral Consider the cornu spiral given by...Ch. 10 - Prob. 8PSCh. 10 - Prob. 9PSCh. 10 - Prob. 10PSCh. 10 - Prob. 11PSCh. 10 - Prob. 12PSCh. 10 - Prob. 13PSCh. 10 - Prob. 14PSCh. 10 - Prob. 15PSCh. 10 - Prob. 16PSCh. 10 - Prob. 17PS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Area of a Sector of a Circle In Exercises 57 and 58, find the area of the sector of a circle of radius r and central angle . r=2.5feet , =225arrow_forwardChange the Cartesian integral into an equivalent polar integral. Then evaluate the polar integral. Cartesian in images* I need the answer for the boxes 1, 2, and 3 and the value of the doublearrow_forwardPolar coordinates are suited to finding the area (choose one): (a) under a curve between x = a and x = b. (b) bounded by a curve and two rays through the origin.arrow_forward
- Use a graphing utility to graph the polar equations. Find the area of the given region analytically.. Inside r = 2 cos θ and outside r = 1arrow_forwardArea in Polar Coordinatesarrow_forward(Using integrals)Find the length of the exterior of the region formed by the union of the following polar equations:arrow_forward
- a) Sketch the region of integration b) Express the region in polar coordinates c) Write an equivalent double integral in polar coordinatesarrow_forwardPlot and determine the area represent between two equations in polar coordinate: r²=2b²cos2 theta ,,,,, and r =b/2arrow_forwardDouble integrals in polar coordinates: Evaluate the iterated integral by converting to polar coordinates. ⌠2⌠√(2x-x²) 4√(x2+y2) dy dx ⌡0⌡0arrow_forward
- Integrals in spherical coordinates Evaluate the following integral in spherical coordinates.arrow_forwardQ/Discuss the determine the area formula in polar coordinate with an example ?arrow_forwardWrite an integral that represents the area of the surface generated by revolving the curve about the x-axis. Use a graphing utility to approximate the integral. Parametric Equations x = cos2 θ, y = cos θ Interval 0 ≤ θ ≤ π/2arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Double and Triple Integrals; Author: Professor Dave Explains;https://www.youtube.com/watch?v=UubU3U2C8WM;License: Standard YouTube License, CC-BY