Chapter 11, Problem 5P
BuyFindarrow_forward
Multivariable Calculus
8th Edition
James Stewart
ISBN: 9781305266643
Solutions
Chapter
Section
BuyFindarrow_forward
Multivariable Calculus
8th Edition
James Stewart
ISBN: 9781305266643
Textbook Problem
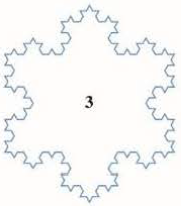
To construct the snowflake curve, start with an equilateral triangle with sides of length 1. Step 1 in the construction is to divide each side into three equal parts, construct an equilateral triangle on the middle part, and then delete the middle part (see the figure). Step 2 is to repeat step 1 for each side of the resulting polygon. This process is repeated at each succeeding step. The snowflake curve is the curve that results from repeating this process indefinitely.
- (a) Let sn, ln, and pn represent the number of sides, the length of a side, and the total length of the nth approximating curve (the curve obtained alter step n of the construction), respectively. Find formulas for sn, ln, and pn.
- (b) Show that pn → ∞ as n → ∞.
- (c) Sum an infinite series to find the area enclosed by the snowflake curve.
Note: Parts (b) and (c) show that the snowflake curve is infinitely long but encloses only a finite area.
FIGURE FOR PROBLEM 5
(a)
To determine
To find: The formula for the number of sides
Explanation
Calculation:
The equilateral triangle each of length,
Therefore the number of sides
In general the number of sides
The length of the side
(b)
To determine
To show: The total length of the
(c)
To determine
To find: The area enclosed by the snow flake curve.
Chapter 11 Solutions
Sect-11.1 P-1ESect-11.1 P-2ESect-11.1 P-3ESect-11.1 P-4ESect-11.1 P-5ESect-11.1 P-6ESect-11.1 P-7ESect-11.1 P-8ESect-11.1 P-9ESect-11.1 P-10E
Sect-11.1 P-11ESect-11.1 P-12ESect-11.1 P-13ESect-11.1 P-14ESect-11.1 P-15ESect-11.1 P-16ESect-11.1 P-17ESect-11.1 P-18ESect-11.1 P-19ESect-11.1 P-20ESect-11.1 P-21ESect-11.1 P-22ESect-11.1 P-23ESect-11.1 P-24ESect-11.1 P-25ESect-11.1 P-26ESect-11.1 P-27ESect-11.1 P-28ESect-11.1 P-29ESect-11.1 P-30ESect-11.1 P-31ESect-11.1 P-32ESect-11.1 P-33ESect-11.1 P-34ESect-11.1 P-35ESect-11.1 P-36ESect-11.1 P-37ESect-11.1 P-38ESect-11.1 P-39ESect-11.1 P-40ESect-11.1 P-41ESect-11.1 P-42ESect-11.1 P-43ESect-11.1 P-44ESect-11.1 P-45ESect-11.1 P-46ESect-11.1 P-47ESect-11.1 P-48ESect-11.1 P-49ESect-11.1 P-50ESect-11.1 P-51ESect-11.1 P-52ESect-11.1 P-53ESect-11.1 P-54ESect-11.1 P-55ESect-11.1 P-56ESect-11.1 P-57ESect-11.1 P-58ESect-11.1 P-59ESect-11.1 P-60ESect-11.1 P-61ESect-11.1 P-62ESect-11.1 P-63ESect-11.1 P-64ESect-11.1 P-65ESect-11.1 P-66ESect-11.1 P-67ESect-11.1 P-68ESect-11.1 P-69ESect-11.1 P-70ESect-11.1 P-71ESect-11.1 P-72ESect-11.1 P-73ESect-11.1 P-74ESect-11.1 P-75ESect-11.1 P-76ESect-11.1 P-77ESect-11.1 P-78ESect-11.1 P-79ESect-11.1 P-80ESect-11.1 P-81ESect-11.1 P-82ESect-11.1 P-83ESect-11.1 P-84ESect-11.1 P-85ESect-11.1 P-86ESect-11.1 P-87ESect-11.1 P-88ESect-11.1 P-89ESect-11.1 P-90ESect-11.1 P-91ESect-11.1 P-92ESect-11.1 P-93ESect-11.2 P-1ESect-11.2 P-2ESect-11.2 P-3ESect-11.2 P-4ESect-11.2 P-5ESect-11.2 P-6ESect-11.2 P-7ESect-11.2 P-8ESect-11.2 P-9ESect-11.2 P-10ESect-11.2 P-11ESect-11.2 P-12ESect-11.2 P-13ESect-11.2 P-14ESect-11.2 P-15ESect-11.2 P-16ESect-11.2 P-17ESect-11.2 P-18ESect-11.2 P-19ESect-11.2 P-20ESect-11.2 P-21ESect-11.2 P-22ESect-11.2 P-23ESect-11.2 P-24ESect-11.2 P-25ESect-11.2 P-26ESect-11.2 P-27ESect-11.2 P-28ESect-11.2 P-29ESect-11.2 P-30ESect-11.2 P-31ESect-11.2 P-32ESect-11.2 P-33ESect-11.2 P-34ESect-11.2 P-35ESect-11.2 P-36ESect-11.2 P-37ESect-11.2 P-38ESect-11.2 P-39ESect-11.2 P-40ESect-11.2 P-41ESect-11.2 P-42ESect-11.2 P-43ESect-11.2 P-44ESect-11.2 P-45ESect-11.2 P-46ESect-11.2 P-47ESect-11.2 P-48ESect-11.2 P-49ESect-11.2 P-50ESect-11.2 P-51ESect-11.2 P-52ESect-11.2 P-53ESect-11.2 P-54ESect-11.2 P-55ESect-11.2 P-56ESect-11.2 P-57ESect-11.2 P-58ESect-11.2 P-59ESect-11.2 P-60ESect-11.2 P-61ESect-11.2 P-62ESect-11.2 P-63ESect-11.2 P-64ESect-11.2 P-67ESect-11.2 P-68ESect-11.2 P-69ESect-11.2 P-70ESect-11.2 P-71ESect-11.2 P-72ESect-11.2 P-73ESect-11.2 P-74ESect-11.2 P-75ESect-11.2 P-76ESect-11.2 P-77ESect-11.2 P-78ESect-11.2 P-79ESect-11.2 P-80ESect-11.2 P-81ESect-11.2 P-82ESect-11.2 P-83ESect-11.2 P-84ESect-11.2 P-85ESect-11.2 P-86ESect-11.2 P-87ESect-11.2 P-88ESect-11.2 P-89ESect-11.2 P-90ESect-11.2 P-91ESect-11.2 P-92ESect-11.3 P-1ESect-11.3 P-2ESect-11.3 P-3ESect-11.3 P-4ESect-11.3 P-5ESect-11.3 P-6ESect-11.3 P-7ESect-11.3 P-8ESect-11.3 P-9ESect-11.3 P-10ESect-11.3 P-11ESect-11.3 P-12ESect-11.3 P-13ESect-11.3 P-14ESect-11.3 P-15ESect-11.3 P-16ESect-11.3 P-17ESect-11.3 P-18ESect-11.3 P-19ESect-11.3 P-20ESect-11.3 P-21ESect-11.3 P-22ESect-11.3 P-23ESect-11.3 P-24ESect-11.3 P-25ESect-11.3 P-26ESect-11.3 P-27ESect-11.3 P-28ESect-11.3 P-29ESect-11.3 P-30ESect-11.3 P-31ESect-11.3 P-32ESect-11.3 P-33ESect-11.3 P-34ESect-11.3 P-35ESect-11.3 P-36ESect-11.3 P-37ESect-11.3 P-38ESect-11.3 P-39ESect-11.3 P-40ESect-11.3 P-41ESect-11.3 P-43ESect-11.3 P-44ESect-11.3 P-45ESect-11.3 P-46ESect-11.4 P-1ESect-11.4 P-2ESect-11.4 P-3ESect-11.4 P-4ESect-11.4 P-5ESect-11.4 P-6ESect-11.4 P-7ESect-11.4 P-8ESect-11.4 P-9ESect-11.4 P-10ESect-11.4 P-11ESect-11.4 P-12ESect-11.4 P-13ESect-11.4 P-14ESect-11.4 P-15ESect-11.4 P-16ESect-11.4 P-17ESect-11.4 P-18ESect-11.4 P-19ESect-11.4 P-20ESect-11.4 P-21ESect-11.4 P-22ESect-11.4 P-23ESect-11.4 P-24ESect-11.4 P-25ESect-11.4 P-26ESect-11.4 P-27ESect-11.4 P-28ESect-11.4 P-29ESect-11.4 P-30ESect-11.4 P-31ESect-11.4 P-32ESect-11.4 P-33ESect-11.4 P-34ESect-11.4 P-35ESect-11.4 P-36ESect-11.4 P-37ESect-11.4 P-38ESect-11.4 P-39ESect-11.4 P-40ESect-11.4 P-41ESect-11.4 P-42ESect-11.4 P-43ESect-11.4 P-44ESect-11.4 P-45ESect-11.4 P-46ESect-11.5 P-1ESect-11.5 P-2ESect-11.5 P-3ESect-11.5 P-4ESect-11.5 P-5ESect-11.5 P-6ESect-11.5 P-7ESect-11.5 P-8ESect-11.5 P-9ESect-11.5 P-10ESect-11.5 P-11ESect-11.5 P-12ESect-11.5 P-13ESect-11.5 P-14ESect-11.5 P-15ESect-11.5 P-16ESect-11.5 P-17ESect-11.5 P-18ESect-11.5 P-19ESect-11.5 P-20ESect-11.5 P-21ESect-11.5 P-22ESect-11.5 P-23ESect-11.5 P-24ESect-11.5 P-25ESect-11.5 P-26ESect-11.5 P-27ESect-11.5 P-28ESect-11.5 P-29ESect-11.5 P-30ESect-11.5 P-31ESect-11.5 P-32ESect-11.5 P-33ESect-11.5 P-34ESect-11.5 P-35ESect-11.5 P-36ESect-11.6 P-1ESect-11.6 P-2ESect-11.6 P-3ESect-11.6 P-4ESect-11.6 P-5ESect-11.6 P-6ESect-11.6 P-7ESect-11.6 P-8ESect-11.6 P-9ESect-11.6 P-10ESect-11.6 P-11ESect-11.6 P-12ESect-11.6 P-13ESect-11.6 P-14ESect-11.6 P-15ESect-11.6 P-16ESect-11.6 P-17ESect-11.6 P-18ESect-11.6 P-19ESect-11.6 P-20ESect-11.6 P-21ESect-11.6 P-22ESect-11.6 P-23ESect-11.6 P-24ESect-11.6 P-25ESect-11.6 P-26ESect-11.6 P-27ESect-11.6 P-28ESect-11.6 P-29ESect-11.6 P-30ESect-11.6 P-31ESect-11.6 P-32ESect-11.6 P-33ESect-11.6 P-34ESect-11.6 P-35ESect-11.6 P-36ESect-11.6 P-37ESect-11.6 P-38ESect-11.6 P-39ESect-11.6 P-40ESect-11.6 P-41ESect-11.6 P-42ESect-11.6 P-43ESect-11.6 P-44ESect-11.6 P-45ESect-11.6 P-46ESect-11.6 P-47ESect-11.6 P-48ESect-11.6 P-49ESect-11.6 P-50ESect-11.6 P-51ESect-11.6 P-52ESect-11.6 P-53ESect-11.7 P-1ESect-11.7 P-2ESect-11.7 P-3ESect-11.7 P-4ESect-11.7 P-5ESect-11.7 P-6ESect-11.7 P-7ESect-11.7 P-8ESect-11.7 P-9ESect-11.7 P-10ESect-11.7 P-11ESect-11.7 P-12ESect-11.7 P-13ESect-11.7 P-14ESect-11.7 P-15ESect-11.7 P-16ESect-11.7 P-17ESect-11.7 P-18ESect-11.7 P-19ESect-11.7 P-20ESect-11.7 P-21ESect-11.7 P-22ESect-11.7 P-23ESect-11.7 P-24ESect-11.7 P-25ESect-11.7 P-26ESect-11.7 P-27ESect-11.7 P-28ESect-11.7 P-29ESect-11.7 P-30ESect-11.7 P-31ESect-11.7 P-32ESect-11.7 P-33ESect-11.7 P-34ESect-11.7 P-35ESect-11.7 P-36ESect-11.7 P-37ESect-11.7 P-38ESect-11.8 P-1ESect-11.8 P-2ESect-11.8 P-3ESect-11.8 P-4ESect-11.8 P-5ESect-11.8 P-6ESect-11.8 P-7ESect-11.8 P-8ESect-11.8 P-9ESect-11.8 P-10ESect-11.8 P-11ESect-11.8 P-12ESect-11.8 P-13ESect-11.8 P-14ESect-11.8 P-15ESect-11.8 P-16ESect-11.8 P-17ESect-11.8 P-18ESect-11.8 P-19ESect-11.8 P-20ESect-11.8 P-21ESect-11.8 P-22ESect-11.8 P-23ESect-11.8 P-24ESect-11.8 P-25ESect-11.8 P-26ESect-11.8 P-27ESect-11.8 P-28ESect-11.8 P-29ESect-11.8 P-30ESect-11.8 P-31ESect-11.8 P-32ESect-11.8 P-33ESect-11.8 P-34ESect-11.8 P-37ESect-11.8 P-38ESect-11.8 P-39ESect-11.8 P-40ESect-11.8 P-41ESect-11.8 P-42ESect-11.9 P-1ESect-11.9 P-2ESect-11.9 P-3ESect-11.9 P-4ESect-11.9 P-5ESect-11.9 P-6ESect-11.9 P-7ESect-11.9 P-8ESect-11.9 P-9ESect-11.9 P-10ESect-11.9 P-11ESect-11.9 P-12ESect-11.9 P-13ESect-11.9 P-14ESect-11.9 P-15ESect-11.9 P-16ESect-11.9 P-17ESect-11.9 P-18ESect-11.9 P-19ESect-11.9 P-20ESect-11.9 P-21ESect-11.9 P-22ESect-11.9 P-23ESect-11.9 P-24ESect-11.9 P-25ESect-11.9 P-26ESect-11.9 P-27ESect-11.9 P-28ESect-11.9 P-29ESect-11.9 P-30ESect-11.9 P-31ESect-11.9 P-32ESect-11.9 P-33ESect-11.9 P-34ESect-11.9 P-35ESect-11.9 P-36ESect-11.9 P-37ESect-11.9 P-38ESect-11.9 P-39ESect-11.9 P-40ESect-11.9 P-41ESect-11.9 P-42ESect-11.10 P-1ESect-11.10 P-2ESect-11.10 P-3ESect-11.10 P-4ESect-11.10 P-5ESect-11.10 P-6ESect-11.10 P-7ESect-11.10 P-8ESect-11.10 P-9ESect-11.10 P-10ESect-11.10 P-11ESect-11.10 P-12ESect-11.10 P-13ESect-11.10 P-14ESect-11.10 P-15ESect-11.10 P-16ESect-11.10 P-17ESect-11.10 P-18ESect-11.10 P-19ESect-11.10 P-20ESect-11.10 P-21ESect-11.10 P-22ESect-11.10 P-23ESect-11.10 P-24ESect-11.10 P-25ESect-11.10 P-26ESect-11.10 P-27ESect-11.10 P-28ESect-11.10 P-29ESect-11.10 P-30ESect-11.10 P-31ESect-11.10 P-32ESect-11.10 P-33ESect-11.10 P-34ESect-11.10 P-35ESect-11.10 P-36ESect-11.10 P-37ESect-11.10 P-38ESect-11.10 P-39ESect-11.10 P-40ESect-11.10 P-41ESect-11.10 P-42ESect-11.10 P-43ESect-11.10 P-44ESect-11.10 P-45ESect-11.10 P-46ESect-11.10 P-47ESect-11.10 P-48ESect-11.10 P-49ESect-11.10 P-50ESect-11.10 P-51ESect-11.10 P-52ESect-11.10 P-53ESect-11.10 P-54ESect-11.10 P-55ESect-11.10 P-56ESect-11.10 P-57ESect-11.10 P-58ESect-11.10 P-59ESect-11.10 P-60ESect-11.10 P-61ESect-11.10 P-62ESect-11.10 P-63ESect-11.10 P-64ESect-11.10 P-65ESect-11.10 P-66ESect-11.10 P-67ESect-11.10 P-68ESect-11.10 P-69ESect-11.10 P-70ESect-11.10 P-71ESect-11.10 P-72ESect-11.10 P-73ESect-11.10 P-74ESect-11.10 P-75ESect-11.10 P-76ESect-11.10 P-77ESect-11.10 P-78ESect-11.10 P-79ESect-11.10 P-80ESect-11.10 P-81ESect-11.10 P-82ESect-11.10 P-83ESect-11.10 P-84ESect-11.10 P-85ESect-11.10 P-86ESect-11.11 P-1ESect-11.11 P-2ESect-11.11 P-3ESect-11.11 P-4ESect-11.11 P-5ESect-11.11 P-6ESect-11.11 P-7ESect-11.11 P-8ESect-11.11 P-9ESect-11.11 P-10ESect-11.11 P-13ESect-11.11 P-14ESect-11.11 P-15ESect-11.11 P-16ESect-11.11 P-17ESect-11.11 P-18ESect-11.11 P-19ESect-11.11 P-20ESect-11.11 P-21ESect-11.11 P-22ESect-11.11 P-23ESect-11.11 P-24ESect-11.11 P-25ESect-11.11 P-26ESect-11.11 P-27ESect-11.11 P-28ESect-11.11 P-29ESect-11.11 P-30ESect-11.11 P-31ESect-11.11 P-32ESect-11.11 P-33ESect-11.11 P-34ESect-11.11 P-35ESect-11.11 P-36ESect-11.11 P-37ESect-11.11 P-38ESect-11.11 P-39ECh-11 P-1RCCCh-11 P-2RCCCh-11 P-3RCCCh-11 P-4RCCCh-11 P-5RCCCh-11 P-6RCCCh-11 P-7RCCCh-11 P-8RCCCh-11 P-9RCCCh-11 P-10RCCCh-11 P-11RCCCh-11 P-12RCCCh-11 P-1RQCh-11 P-2RQCh-11 P-3RQCh-11 P-4RQCh-11 P-5RQCh-11 P-6RQCh-11 P-7RQCh-11 P-8RQCh-11 P-9RQCh-11 P-10RQCh-11 P-11RQCh-11 P-12RQCh-11 P-13RQCh-11 P-14RQCh-11 P-15RQCh-11 P-16RQCh-11 P-17RQCh-11 P-18RQCh-11 P-19RQCh-11 P-20RQCh-11 P-21RQCh-11 P-22RQCh-11 P-1RECh-11 P-2RECh-11 P-3RECh-11 P-4RECh-11 P-5RECh-11 P-6RECh-11 P-7RECh-11 P-8RECh-11 P-9RECh-11 P-10RECh-11 P-11RECh-11 P-12RECh-11 P-13RECh-11 P-14RECh-11 P-15RECh-11 P-16RECh-11 P-17RECh-11 P-18RECh-11 P-19RECh-11 P-20RECh-11 P-21RECh-11 P-22RECh-11 P-23RECh-11 P-24RECh-11 P-25RECh-11 P-26RECh-11 P-27RECh-11 P-28RECh-11 P-29RECh-11 P-30RECh-11 P-31RECh-11 P-32RECh-11 P-33RECh-11 P-34RECh-11 P-35RECh-11 P-36RECh-11 P-37RECh-11 P-38RECh-11 P-39RECh-11 P-40RECh-11 P-41RECh-11 P-42RECh-11 P-43RECh-11 P-44RECh-11 P-45RECh-11 P-46RECh-11 P-47RECh-11 P-48RECh-11 P-49RECh-11 P-50RECh-11 P-51RECh-11 P-52RECh-11 P-53RECh-11 P-54RECh-11 P-55RECh-11 P-56RECh-11 P-57RECh-11 P-58RECh-11 P-59RECh-11 P-60RECh-11 P-61RECh-11 P-62RECh-11 P-1PCh-11 P-2PCh-11 P-3PCh-11 P-4PCh-11 P-5PCh-11 P-6PCh-11 P-7PCh-11 P-8PCh-11 P-9PCh-11 P-10PCh-11 P-11PCh-11 P-12PCh-11 P-13PCh-11 P-14PCh-11 P-15PCh-11 P-16PCh-11 P-17PCh-11 P-18PCh-11 P-19PCh-11 P-20PCh-11 P-21PCh-11 P-22PCh-11 P-23PCh-11 P-24PCh-11 P-25PCh-11 P-26P
Additional Math Solutions
Find more solutions based on key concepts
Show solutions addConvert each expression in Exercises 25-50 into its technology formula equivalent as in the table in the text. ...
Finite Mathematics and Applied Calculus (MindTap Course List)
Evaluating Limits Use a graphing utility to evaluate limx0tannxx
Calculus: Early Transcendental Functions
Find equations of the lines that pass through the point (3, 5) and are (a) parallel to the line x + 4y = -2. (b...
Calculus: An Applied Approach (MindTap Course List)
Distance, Speed, and Time A pilot flew a jet from Montreal to Los Angeles, a distance of 2500 mi. On the return...
Precalculus: Mathematics for Calculus (Standalone Book)
Use the guidelines of this section to sketch the curve. y=xx24
Single Variable Calculus: Early Transcendentals, Volume I
Sketch the graph of the function. 47. g(t) = |1 3t|
Calculus: Early Transcendentals
CJ About half of the police officers in Shinbone, Kansas, have completed a special course in investigative proc...
Essentials Of Statistics
A population of N = 7 scores has a mean of = 13. What is the value of X for this population?
Essentials of Statistics for The Behavioral Sciences (MindTap Course List)
20-27 Sketch the graph of a function that satisfies all of the given conditions. f(x)0forallx1, vertical asympt...
Calculus (MindTap Course List)
A distribution with a mean of =38and a standard deviation of =5is transformed into a standardized distribution ...
Statistics for The Behavioral Sciences (MindTap Course List)
In Exercises 99-106, factor out the greatest common factor from each expression. 106. 12(23u3/22u1/2)
Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach
For the function A whose graph is shown, state the following. (a) limx3A(x) (b) limx2A(x) (c) limx2+A(x)` (d) l...
Single Variable Calculus
Fishing: Levels of Measurement Categorize these measurements associated with fishing according to level: nomina...
Understanding Basic Statistics
For Problems 55-64, answer the question with an algebraic expression. Celia has p pennies, n nickels, and q qua...
Intermediate Algebra
Some parts of California are particularly earthquake-prone. Suppose that in one metropolitan area. 25% of all h...
Probability and Statistics for Engineering and the Sciences
Convert each expression in Exercises 25-50 into its technology formula equivalent as in the table in the text. ...
Finite Mathematics
27. Two different investment companies offer college savings plans, one at 8.2% compounded continuously and the...
Mathematical Applications for the Management, Life, and Social Sciences
Raise the following fractions to higher terms as indicated. 23totwenty-sevenths23=1827__(273=992=18)
Contemporary Mathematics for Business & Consumers
In Exercises 11 to 16, the drawing shows trapezoid ABCD with ABDC ; also, M and N are midpoints of AD and BC , ...
Elementary Geometry For College Students, 7e
In Exercises 37 to 48, use set-builder notation to write each of the following sets. {January, March, May, July...
Mathematical Excursions (MindTap Course List)
Perform the indicated operations and simplify: 383516
Elementary Technical Mathematics
Fixed Point Use the result of Exercise 81 to show that f(x)=12cosx has at most one fixed point.
Calculus of a Single Variable
Using a Product-to-Sum Formula In Exercises 43-48, find the indefinite integral. cos5cos3d
Calculus: Early Transcendental Functions (MindTap Course List)
(a) What can you say about the graph of a solution of the equation y = xy3 when x is close to 0? What if x is l...
Single Variable Calculus: Early Transcendentals
For Problems 55 through 60, round your answers to the nearest tenth of a unit when necessary. Find the circumfe...
Trigonometry (MindTap Course List)
Label each of the following statements as either true or false. [ a ][ x ]=[ a ][ y ] and [ a ][ 0 ] implies [ ...
Elements Of Modern Algebra
An integral for the solid obtained by rotating the region at the right about the x-axis is:
Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th
True or False: If a number p is in the interval of convergence of then so is the number .
Study Guide for Stewart's Multivariable Calculus, 8th
The paper The Effects of Split Keyboard Geometry un Upper Body Postures (Ergonomics [2009]: 104111) describes a...
Introduction To Statistics And Data Analysis
Find a the exact length of an ideal rectangle with width W = 5 by solving 5L=L55. b the approximate length of a...
Elementary Geometry for College Students
In Exercise 16, find the value of the probability of the standard normal variable Z corresponding to the shaded...
Finite Mathematics for the Managerial, Life, and Social Sciences
Domain Find all values of c such that the domain of f(x)=x+3x2+3cx+6 is the set of all real numbers.
Calculus
Finding the Area of a Polar Region Between Two Curves In Exercises 37-44, use a graphing utility to graph the p...
Calculus (MindTap Course List)
Finding Volume In Exercises 29-34, set up and evaluate a double integral to find the volume of the solid bounde...
Multivariable Calculus
Describe the difference between inductive and deductive reasoning and give an example of each.
Research Methods for the Behavioral Sciences (MindTap Course List)
In the following table, the lengths of the sides of cubes are given. Determine the volumes of the cubes. Round ...
Mathematics For Machine Technology
The national highway Traffic Safety administration reported the percentage of traffic accidents occurring each ...
STATISTICS F/BUSINESS+ECONOMICS-TEXT
Write the equation for the graph of the function shown.
College Algebra (MindTap Course List)
In Exercise 17 and 18, use the following information: To determine what effect salespeople had on purchases, a ...
Mathematics: A Practical Odyssey
The Nielsen Home Technology Report provided information about home technology and its usage. The following data...
Statistics for Business & Economics, Revised (MindTap Course List)
According to the gamblers fallacy, if a coin toss results in heads three times in a row, then the probability o...
Research Methods for the Behavioral Sciences (MindTap Course List)
