The Heart of Mathematics: An Invitation to Effective Thinking
4th Edition
ISBN: 9781118156599
Author: Edward B. Burger, Michael Starbird
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 4.6, Problem 4MS
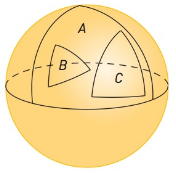
A triangular trio. The sphere below has three triangles on it. For which triangle is the sum of the angles largest? For which triangle is the sum smallest?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Test the claim that a student's pulse rate is different when taking a quiz than attending a regular class. The mean pulse rate difference is 2.7 with 10 students. Use a significance level of 0.005.
Pulse rate difference(Quiz - Lecture)
2
-1
5
-8
1
20
15
-4
9
-12
There are three options for investing $1150. The first earns 10% compounded annually, the second earns 10% compounded quarterly, and the third earns 10% compounded continuously. Find equations that model each investment growth and
use a graphing utility to graph each model in the same viewing window over a 20-year period. Use the graph to determine which investment yields the highest return after 20 years. What are the differences in earnings among the three
investment?
STEP 1: The formula for compound interest is
A =
nt
= P(1 + − − ) n²,
where n is the number of compoundings per year, t is the number of years, r is the interest rate, P is the principal, and A is the amount (balance) after t years. For continuous compounding, the formula reduces to
A = Pert
Find r and n for each model, and use these values to write A in terms of t for each case.
Annual Model
r=0.10
A = Y(t) = 1150 (1.10)*
n = 1
Quarterly Model
r = 0.10
n = 4
A = Q(t) = 1150(1.025) 4t
Continuous Model
r=0.10
A = C(t) =…
The following ordered data list shows the data speeds for cell phones used by a
telephone company at an airport:
A. Calculate the Measures of Central Tendency from the ungrouped data list.
B. Group the data in an appropriate frequency table.
C. Calculate the Measures of Central Tendency using the table in point B.
D. Are there differences in the measurements obtained in A and C? Why (give at
least one justified reason)?
I leave the answers to A and B to resolve the remaining two.
0.8
1.4
1.8
1.9
3.2
3.6
4.5
4.5
4.6
6.2
6.5
7.7
7.9
9.9
10.2
10.3
10.9
11.1
11.1
11.6
11.8
12.0
13.1
13.5
13.7
14.1
14.2
14.7
15.0
15.1
15.5
15.8
16.0
17.5
18.2
20.2
21.1
21.5
22.2
22.4
23.1
24.5
25.7
28.5
34.6
38.5
43.0
55.6
71.3
77.8
A. Measures of Central Tendency
We are to calculate:
Mean, Median, Mode
The data (already ordered) is:
0.8, 1.4, 1.8, 1.9, 3.2, 3.6, 4.5, 4.5, 4.6, 6.2, 6.5, 7.7, 7.9, 9.9, 10.2, 10.3, 10.9,
11.1, 11.1, 11.6,
11.8, 12.0, 13.1, 13.5, 13.7, 14.1, 14.2, 14.7, 15.0, 15.1, 15.5,…
Chapter 4 Solutions
The Heart of Mathematics: An Invitation to Effective Thinking
Ch. 4.1 - The main event. State the Pythagorean Theorem.Ch. 4.1 - Two out of three. If a right triangle has legs of...Ch. 4.1 - Hypotenuse hype. If a right triangle has legs of...Ch. 4.1 - Assesing area. Suppose you know the base of a...Ch. 4.1 - Squares all around. How does the figure below...Ch. 4.1 - Operating on the triangle. Using a straightedge,...Ch. 4.1 - Excite your friends about right triangles....Ch. 4.1 - Easy as 1,2,3? Can there be a right triangle with...Ch. 4.1 - Sky high (S). On a sunny, warm day, a student...Ch. 4.1 - Sand masting (H). The sailboat named Sand Bug has...
Ch. 4.1 - Getting a pole on a bus. For his 13th birthday,...Ch. 4.1 - The Scarecrow (ExH). In the 1939 movie The Wizard...Ch. 4.1 - Rooting through a spiral. Start with a right...Ch. 4.1 - Is it right? (H) Suppose someone tells you that...Ch. 4.1 - Tfrain trouble (H). Train tracks are made of...Ch. 4.1 - Does everyone have what it takes to be a triangle?...Ch. 4.1 - Getting squared away. In our proof of the...Ch. 4.1 - The practical side of Pythagoras. Suppose you are...Ch. 4.1 - Pythagorean pizzas (H). You have a choice at the...Ch. 4.1 - Natural right (S). Suppose r and s are any two...Ch. 4.1 - Well-rounded shapes. Suppose we have two circles...Ch. 4.1 - A Pythagorean Theorem for triangles other than...Ch. 4.1 - With a group of folks. In a small group, discuss...Ch. 4.1 - Double trouble. Suppose you know a right triangle...Ch. 4.1 - K-ple trouble. Suppose you have a right triangle...Ch. 4.1 - Padding around. You have a rectangular patio with...Ch. 4.1 - Pythagoras goes the distance. Plot the points (5,...Ch. 4.1 - Ahoy there! (H) Your exotic sailboat, which you...Ch. 4.2 - Standing guard. Draw the floor plan of a gallery...Ch. 4.2 - Art appreciation. State the Art Gallery Theorem.Ch. 4.2 - Upping the ante. How many guards do you need for a...Ch. 4.2 - Keep it safe. At what vertices would you place...Ch. 4.2 - Puttoing guards in their place. For each floor...Ch. 4.2 - Guarding the Guggenheim. The Art Gallery Theorem...Ch. 4.2 - TriangulatIng the Louvre (H). Triangulate the...Ch. 4.2 - Triangulating the Clark. Triangulate the floor...Ch. 4.2 - Tricolor me (ExH). For each triangulation, color...Ch. 4.2 - Tricolor hue. For each triangulation, color the...Ch. 4.2 - One-third. Write the number 6 as a sum of three...Ch. 4.2 - Easy watch. Draw a floor plan of a museum with six...Ch. 4.2 - Two watches (S). Draw the floor plan of a museum...Ch. 4.2 - Mirror, mirror on the wall. Consider the floor...Ch. 4.2 - Nine needs three (H). Draw a floor plan for a...Ch. 4.2 - One-third again (ExH). If a natural number is...Ch. 4.2 - Square museum (S). If a museum has only...Ch. 4.2 - Worst squares (H). Draw examples of museums with...Ch. 4.2 - Pie are squared. The circumference of a circle of...Ch. 4.2 - I can see the light. Suppose you are in a...Ch. 4.2 - Less than. Youve tnangulated your polygon and...Ch. 4.2 - Greater than. Youve triangulated your polygon and...Ch. 4.2 - Counting the colors. Your polygon has 40 vertices....Ch. 4.2 - Only red. Twelve of your polygons vertices have...Ch. 4.2 - Totaling triangles. If a polygon has n sides, it...Ch. 4.3 - Defining gold. Explain what makes a rectangle a...Ch. 4.3 - Approximating gold. Which of these numbers is...Ch. 4.3 - Approximating again. Which of the following...Ch. 4.3 - Same solution. Why does the equation l1=1l have...Ch. 4.3 - X marks the unkonw (ExH). Solve eachh equation for...Ch. 4.3 - A cold tall one? Can a Golden Rectangle have a...Ch. 4.3 - Fold the gold (H). Suppose you have a Golden...Ch. 4.3 - Sheets of gold. Suppose you have two sheets of...Ch. 4.3 - Circular logic? (H). Take a Golden Rectangle and...Ch. 4.3 - Growing gold (H). Take a Golden Rectangle and...Ch. 4.3 - Counterfeit gold? Draw a rectangle with its longer...Ch. 4.3 - In the grid (S). Consider the 1010 grid at left....Ch. 4.3 - A nest of gold. Consider the figure of infinitely...Ch. 4.3 - Comparing areas (ExH). Let G be a Golden Rectangle...Ch. 4.3 - Do we get gold? Lets make a rectangle somewhat...Ch. 4.3 - Do we get gold this time? (S) We now describe...Ch. 4.3 - A silver lining? (H) Consider the diagonal in the...Ch. 4.3 - Prob. 20MSCh. 4.3 - Going platinum. Determine the dimensions of a...Ch. 4.3 - Golden triangles. Draw a right triangle with one...Ch. 4.3 - Prob. 23MSCh. 4.3 - Prob. 24MSCh. 4.3 - Prob. 25MSCh. 4.3 - Power beyond the mathematics. Provide several...Ch. 4.3 - Special K. As a student at the University of...Ch. 4.3 - Special x. Find all values of x satisfying the...Ch. 4.3 - In search of x. Solve each equation for x:...Ch. 4.3 - Adding a square. Your school Healthy Eating garden...Ch. 4.3 - Golden Pythagoras (H). If you have a Golden...Ch. 4.4 - To tile or not to tile. Which of the following...Ch. 4.4 - Shifting Into symmetry. Shown below are small...Ch. 4.4 - Prob. 3MSCh. 4.4 - Prob. 4MSCh. 4.4 - Symmetric scaling (ExH). Each of the two patterns...Ch. 4.4 - Build a super. Draw a 1,2,5 right triangle in the...Ch. 4.4 - Another angle. Look at the 5-unit super-tile you...Ch. 4.4 - Super-super. Surround your 5-unit super-tile with...Ch. 4.4 - Expand forever (H). If you continue the process of...Ch. 4.4 - Prob. 10MSCh. 4.4 - Expand again. Take your 4.unit equilateral...Ch. 4.4 - One-answer supers. Here is a Pinwheel Pattern. For...Ch. 4.4 - Prob. 14MSCh. 4.4 - Many answer supers (H). Shown here are pictures of...Ch. 4.4 - Fill er up? (ExH) For each tile below, could...Ch. 4.4 - Prob. 18MSCh. 4.4 - Prob. 19MSCh. 4.4 - Prob. 20MSCh. 4.4 - Penrose tiles. Roger Penrose constructed two tiles...Ch. 4.4 - Expand forever. Why does any shape that can be...Ch. 4.4 - Super total. Recall that the Pinwheel Triangle has...Ch. 4.4 - Prob. 26MSCh. 4.4 - XY-tiles. The trapezoidal tile on the left has one...Ch. 4.4 - School spirit. Your dorm bathroom is tiled using...Ch. 4.4 - T-total (H). Suppose you start with one small...Ch. 4.5 - Its nice to be regular. What makes a polygon a...Ch. 4.5 - Keeping it Platonic. What makes a solid a regular...Ch. 4.5 - Countem up. How many faces, edges, and vertices...Ch. 4.5 - Defending duality. Explain why the cube and the...Ch. 4.5 - The eye of the beholder. Suppose you have models...Ch. 4.5 - Drawing solids. Draw each solid by completing the...Ch. 4.5 - Count. For each of the regular solids, take the...Ch. 4.5 - Soccer counts (ExH). Look at a soccer ball. Take...Ch. 4.5 - A solid slice (S). For each regular solid, imagine...Ch. 4.5 - Siding on the cube. Suppose we start with the...Ch. 4.5 - Cube slices (H). Consider slicing the cube with a...Ch. 4.5 - Dual quads (S). Suppose you have a cube with edges...Ch. 4.5 - Super dual. Suppose you take a cube with edges of...Ch. 4.5 - Self-duals. Suppose you have a tetrahedron having...Ch. 4.5 - Not quite regular (ExH). Suppose you allow...Ch. 4.5 - Truncated solids. Slice off all the vertices of...Ch. 4.5 - Stellated solids. Take each regular solid and...Ch. 4.5 - Prob. 24MSCh. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.5 - Here we celeb rate the power of algebra as a...Ch. 4.6 - Walkind the walk. Here are three walks from corner...Ch. 4.6 - Missing angle in action. The triangles below are...Ch. 4.6 - Slippery X. A triangle is drawn on a sphere. Can...Ch. 4.6 - A triangular trio. The sphere below has three...Ch. 4.6 - Saddle sores. The triangle at right is drawn on a...Ch. 4.6 - Travel agent. In each of the following three...Ch. 4.6 - Travel agent. In each of the following three...Ch. 4.6 - Travel agent. In each of the following three...Ch. 4.6 - Latitude losers (H). In each of the following...Ch. 4.6 - Latitude losers (H). In each of the following...Ch. 4.6 - Latitude losers (H). In each of the following...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Spider and bug. For each pair of points on the...Ch. 4.6 - Big angles (H). What is the largest value we can...Ch. 4.6 - Many angles (S). Draw three different great...Ch. 4.6 - Quads in a plane. Measure the sum of the angles of...Ch. 4.6 - Quads on the sphere. Below are quadrilaterals on...Ch. 4.6 - Parallel lines (ExH). On a plane, if you draw a...Ch. 4.6 - Cubical spheres (ExH). Take a cube. Put a point in...Ch. 4.6 - Tetrahedral spheres. Lets do a similar calculation...Ch. 4.6 - Dodecahedral spheres. This Mindscape is the same...Ch. 4.6 - Total excess. Using the observations from the...Ch. 4.6 - What is the sum of the three angles? Why? Consider...Ch. 4.6 - What is the sum of the angles of your triangle? Is...Ch. 4.6 - Removing a slice of the pie. Complete the...Ch. 4.6 - Conjuring up a conjecture. Make a conjecture about...Ch. 4.6 - Tetrahedral angles. What is the sum of the angles...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.6 - Here we celebrate the power of algebra as a...Ch. 4.7 - At one with the univers. Below is a sketch of a...Ch. 4.7 - Are we there yet? Why does the information x=4 not...Ch. 4.7 - Plain places. Plot the following points in the...Ch. 4.7 - Big stack. If you take a huge number of sheets of...Ch. 4.7 - A bigger stack. If you take a huge number of...Ch. 4.7 - On the level in two dimensions. Pictured in the...Ch. 4.7 - On the level in two dimensions (S). Pictured in...Ch. 4.7 - On the level in four dimensions. Pictured in the...Ch. 4.7 - Tearible 2s. In the pictures below, describe how...Ch. 4.7 - Dare not to tear? For the figures in the Tearible...Ch. 4.7 - Unlinking (H). Using the fourth dimension,...Ch. 4.7 - Unknotting. Describe how you would unknot the...Ch. 4.7 - Prob. 13MSCh. 4.7 - Edgy hypercubes (H). Produce drawings of the...Ch. 4.7 - Prob. 15MSCh. 4.7 - Prob. 16MSCh. 4.7 - Doughnuts in dimensions. Suppose we have a...Ch. 4.7 - Assembly required (S). As promised in the...Ch. 4.7 - Slicing the cube. Take a 3-dimensional cube...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...Ch. 4.7 - Here we celebrate the power of algebra as a...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Fill in each blank so that the resulting statement is true. The quadratic function f(x)=a(xh)2+k,a0, is in ____...
Algebra and Trigonometry (6th Edition)
To identify the given transformation as a translation or a reflection where the green image is the original.
Pre-Algebra Student Edition
The 16 sequences in the sample space S.
Probability And Statistical Inference (10th Edition)
Prove the generalized version of the basic counting principle.
A First Course in Probability (10th Edition)
Fill in each blank so that the resulting statement is true.
1. A combination of numbers, variables, and opera...
College Algebra (7th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- A tournament is a complete directed graph, for each pair of vertices x, y either (x, y) is an arc or (y, x) is an arc. One can think of this as a round robin tournament, where the vertices represent teams, each pair plays exactly once, with the direction of the arc indicating which team wins. (a) Prove that every tournament has a direct Hamiltonian path. That is a labeling of the teams V1, V2,..., Un so that vi beats Vi+1. That is a labeling so that team 1 beats team 2, team 2 beats team 3, etc. (b) A digraph is strongly connected if there is a directed path from any vertex to any other vertex. Equivalently, there is no partition of the teams into groups A, B so that every team in A beats every team in B. Prove that every strongly connected tournament has a directed Hamiltonian cycle. Use this to show that for any team there is an ordering as in part (a) for which the given team is first. (c) A king in a tournament is a vertex such that there is a direct path of length at most 2 to any…arrow_forwardUse a graphing utility to find the point of intersection, if any, of the graphs of the functions. Round your result to three decimal places. (Enter NONE in any unused answer blanks.) y = 100e0.01x (x, y) = y = 11,250 ×arrow_forwardhow to construct the following same table?arrow_forward
- The following is known. The complete graph K2t on an even number of vertices has a 1- factorization (equivalently, its edges can be colored with 2t - 1 colors so that the edges incident to each vertex are distinct). This implies that the complete graph K2t+1 on an odd number of vertices has a factorization into copies of tK2 + K₁ (a matching plus an isolated vertex). A group of 10 people wants to set up a 45 week tennis schedule playing doubles, each week, the players will form 5 pairs. One of the pairs will not play, the other 4 pairs will each play one doubles match, two of the pairs playing each other and the other two pairs playing each other. Set up a schedule with the following constraints: Each pair of players is a doubles team exactly 4 times; during those 4 matches they see each other player exactly once; no two doubles teams play each other more than once. (a) Find a schedule. Hint - think about breaking the 45 weeks into 9 blocks of 5 weeks. Use factorizations of complete…arrow_forward. The two person game of slither is played on a graph. Players 1 and 2 take turns, building a path in the graph. To start, Player 1 picks a vertex. Player 2 then picks an edge incident to the vertex. Then, starting with Player 1, players alternate turns, picking a vertex not already selected that is adjacent to one of the ends of the path created so far. The first player who cannot select a vertex loses. (This happens when all neighbors of the end vertices of the path are on the path.) Prove that Player 2 has a winning strategy if the graph has a perfect matching and Player 1 has a winning strategy if the graph does not have a perfect matching. In each case describe a strategy for the winning player that guarantees that they will always be able to select a vertex. The strategy will be based on using a maximum matching to decide the next choice, and will, for one of the cases involve using the fact that maximality means no augmenting paths. Warning, the game slither is often described…arrow_forwardLet D be a directed graph, with loops allowed, for which the indegree at each vertex is at most k and the outdegree at each vertex is at most k. Prove that the arcs of D can be colored so that the arcs entering each vertex must have distinct colors and the arcs leaving each vertex have distinct colors. An arc entering a vertex may have the same color as an arc leaving it. It is probably easiest to make use of a known result about edge coloring. Think about splitting each vertex into an ‘in’ and ‘out’ part and consider what type of graph you get.arrow_forward
- 3:56 wust.instructure.com Page 0 Chapter 5 Test Form A of 2 - ZOOM + | Find any real numbers for which each expression is undefined. 2x 4 1. x Name: Date: 1. 3.x-5 2. 2. x²+x-12 4x-24 3. Evaluate when x=-3. 3. x Simplify each rational expression. x²-3x 4. 2x-6 5. x²+3x-18 x²-9 6. Write an equivalent rational expression with the given denominator. 2x-3 x²+2x+1(x+1)(x+2) Perform the indicated operation and simplify if possible. x²-16 x-3 7. 3x-9 x²+2x-8 x²+9x+20 5x+25 8. 4.x 2x² 9. x-5 x-5 3 5 10. 4x-3 8x-6 2 3 11. x-4 x+4 x 12. x-2x-8 x²-4 ← -> Copyright ©2020 Pearson Education, Inc. + 5 4. 5. 6. 7. 8. 9. 10. 11. 12. T-97arrow_forwardplease work out more details give the solution.arrow_forwardProblem #5 Suppose you flip a two sided fair coin ("heads" or "tails") 8 total times. a). How many ways result in 6 tails and 2 heads? b). How many ways result in 2 tails and 6 heads? c). Compare your answers to part (a) and (b) and explain in a few sentences why the comparison makes sense.arrow_forward
- Burger Dome sells hamburgers, cheeseburgers, french fries, soft drinks, and milk shakes, as well as a limited number of specialty items and dessert selections. Although Burger Dome would like to serve each customer immediately, at times more customers arrive than can be handled by the Burger Dome food service staff. Thus, customers wait in line to place and receive their orders. Burger Dome analyzed data on customer arrivals and concluded that the arrival rate is 30 customers per hour. Burger Dome also studied the order-filling process and found that a single employee can process an average of 44 customer orders per hour. Burger Dome is concerned that the methods currently used to serve customers are resulting in excessive waiting times and a possible loss of sales. Management wants to conduct a waiting line study to help determine the best approach to reduce waiting times and improve service. Suppose Burger Dome establishes two servers but arranges the restaurant layout so that an…arrow_forwardPEER REPLY 1: Choose a classmate's Main Post. 1. Indicate a range of values for the independent variable (x) that is reasonable based on the data provided. 2. Explain what the predicted range of dependent values should be based on the range of independent values.arrow_forwardNote: A waiting line model solver computer package is needed to answer these questions. The Kolkmeyer Manufacturing Company uses a group of six identical machines, each of which operates an average of 18 hours between breakdowns. With randomly occurring breakdowns, the Poisson probability distribution is used to describe the machine breakdown arrival process. One person from the maintenance department provides the single-server repair service for the six machines. Management is now considering adding two machines to its manufacturing operation. This addition will bring the number of machines to eight. The president of Kolkmeyer asked for a study of the need to add a second employee to the repair operation. The service rate for each individual assigned to the repair operation is 0.50 machines per hour. (a) Compute the operating characteristics if the company retains the single-employee repair operation. (Round your answers to four decimal places. Report time in hours.) La = L = Wa = W =…arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Quadrilaterals: Missing Angles and Sides; Author: rhornfeck;https://www.youtube.com/watch?v=knVj1O0L2TM;License: Standard YouTube License, CC-BY
STD IX | State Board | Types of Quadrilateral; Author: Robomate;https://www.youtube.com/watch?v=wh0KQ4UB0EU;License: Standard YouTube License, CC-BY