
Concept explainers
Determine the real root of
(a) Graphically.
(b) Using bisection to determine the root to
(c) Perform the same computation as in (b) but use the false-position method and
(a)
The real roots of the equation
Answer to Problem 3P
Solution:
The approximate real root of the equation is 0.6.
Explanation of Solution
Given Information:
The equation
Calculation:
The graph of the function can be plotted using MATLAB.
Code:
Output:
This gives the following plot:
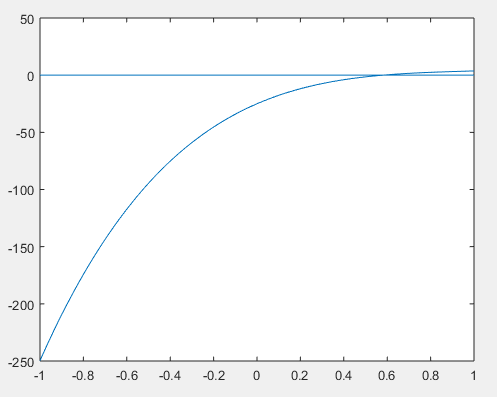
The roots of an equation can be represented graphically by the x-coordinate of the point where the graph cuts the x-axis. From the plot, the only zeros of the equation can be approximated as 0.6.
(b)
To calculate: The root of the equation
Solution:
The root of the equation can be approximated as 0.59375.
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the bisection method as follows:
1. Choose 2 values x, say a andb such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
Now,
Thus,
Now, the second root would be:
The approximate error can be computed as:
The approximate relative percentage error is 200%.
Now,
Thus,
Now, the third root would be:
The approximate error can be computed as:
The approximate error is 11.1%.
Now,
Thus,
Now, the fourth root would be:
The approximate error can be computed as:
The approximate error is 5.26%.
As
(c)
To calculate: The root of the equation
Solution:
The root of the equation can be approximated as 0.57956.
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the false-position method as follows:
1. Choose 2 values x, say a andb such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
Now,
Thus,
Now, the second root would be:
The approximate error can be computed as:
The approximate relative percentage error is 200%.
Now,
Thus,
Now, the third root would be:
The approximate error can be computed as:
The approximate error is 1.29%.
Now,
Thus,
Now, the fourth root would be:
The approximate error can be computed as:
The approximate error is 0.17%.
As
(b)
To calculate: The root of the equation
Answer to Problem 3P
Solution:
The root of the equation can be approximated as 0.59375.
Explanation of Solution
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the bisection method as follows:
1. Choose 2 values x, say a andb such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
Now,
Thus,
Now, the second root would be:
The approximate error can be computed as:
The approximate relative percentage error is 200%.
Now,
Thus,
Now, the third root would be:
The approximate error can be computed as:
The approximate error is 11.1%.
Now,
Thus,
Now, the fourth root would be:
The approximate error can be computed as:
The approximate error is 5.26%.
As
(c)
To calculate: The root of the equation
Solution:
The root of the equation can be approximated as 0.57956.
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the false-position method as follows:
1. Choose 2 values x, say a andb such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
Now,
Thus,
Now, the second root would be:
The approximate error can be computed as:
The approximate relative percentage error is 200%.
Now,
Thus,
Now, the third root would be:
The approximate error can be computed as:
The approximate error is 1.29%.
Now,
Thus,
Now, the fourth root would be:
The approximate error can be computed as:
The approximate error is 0.17%.
As
(c)
To calculate: The root of the equation
Answer to Problem 3P
Solution:
The root of the equation can be approximated as 0.57956.
Explanation of Solution
Given Information:
The equation
Formula Used:
A root of an equation can be obtained using the false-position method as follows:
1. Choose 2 values x, say a andb such that
2. Now, estimate the root by
3. If,
Calculation:
For the provided function:
Hence,
Now take the first root to be,
Now,
Thus,
Now, the second root would be:
The approximate error can be computed as:
The approximate relative percentage error is 200%.
Now,
Thus,
Now, the third root would be:
The approximate error can be computed as:
The approximate error is 1.29%.
Now,
Thus,
Now, the fourth root would be:
The approximate error can be computed as:
The approximate error is 0.17%.
As
Want to see more full solutions like this?
Chapter 5 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
Advanced Engineering Mathematics
Basic Technical Mathematics
Fundamentals of Differential Equations (9th Edition)
Calculus for Business, Economics, Life Sciences, and Social Sciences (13th Edition)
Pre-Algebra Student Edition
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning



