
Calculus (MindTap Course List)
8th Edition
ISBN: 9781285740621
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 5.4, Problem 24E
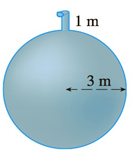
A tank is full of water. Find the work required to pump the water out of the spout. In Exercises 25 and 26 use the fact that water weighs
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 5 Solutions
Calculus (MindTap Course List)
Ch. 5.1 - Find the area of the shaded region.Ch. 5.1 - Find the area of the shaded region.Ch. 5.1 - Prob. 3ECh. 5.1 - Find the area of the shaded region.Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Prob. 10E
Ch. 5.1 - Sketch the region enclosed by the given curves....Ch. 5.1 - Prob. 12ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 14ECh. 5.1 - Prob. 15ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 19ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 21ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 26ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 29ECh. 5.1 - Sketch the region enclosed by the given curves and...Ch. 5.1 - Prob. 31ECh. 5.1 - Prob. 32ECh. 5.1 - Prob. 33ECh. 5.1 - Prob. 34ECh. 5.1 - Prob. 35ECh. 5.1 - Evaluate the integral and interpret it as the area...Ch. 5.1 - Use a graph to find approximate x-coordinates of...Ch. 5.1 - Prob. 38ECh. 5.1 - Prob. 39ECh. 5.1 - Prob. 40ECh. 5.1 - Prob. 41ECh. 5.1 - Prob. 42ECh. 5.1 - Graph the region between the curves and use your...Ch. 5.1 - Prob. 44ECh. 5.1 - Prob. 45ECh. 5.1 - Prob. 46ECh. 5.1 - Prob. 47ECh. 5.1 - The widths in meters of a kidney-shaped swimming...Ch. 5.1 - A cross-section of an airplane wing is shown....Ch. 5.1 - If the birth rate of a population is...Ch. 5.1 - Prob. 51ECh. 5.1 - Prob. 52ECh. 5.1 - Two cars, A and B, start side by side and...Ch. 5.1 - The figure shows graphs of the marginal revenue...Ch. 5.1 - Prob. 55ECh. 5.1 - Prob. 56ECh. 5.1 - Find the number b such that the line y=b divides...Ch. 5.1 - a Find the number a such that the line x=a bisects...Ch. 5.1 - Find the values of c such that the area of the...Ch. 5.1 - Prob. 60ECh. 5.1 - Sketch the region bounded by the given curves and...Ch. 5.1 - Prob. 62ECh. 5.1 - Prob. 63ECh. 5.1 - For what values of m do the line y=mx and the...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 3ECh. 5.2 - Prob. 4ECh. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 6ECh. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 8ECh. 5.2 - Prob. 9ECh. 5.2 - Prob. 10ECh. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Prob. 16ECh. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Find the volume of the solid obtained by rotating...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 22ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 24ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 26ECh. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Refer to the figure and find the volume generated...Ch. 5.2 - Prob. 31ECh. 5.2 - Prob. 32ECh. 5.2 - Set up an integral for the volume of the solid...Ch. 5.2 - Set up an integral for the volume of the solid...Ch. 5.2 - Prob. 35ECh. 5.2 - Prob. 36ECh. 5.2 - Prob. 37ECh. 5.2 - Prob. 38ECh. 5.2 - Prob. 39ECh. 5.2 - Prob. 40ECh. 5.2 - Prob. 41ECh. 5.2 - Prob. 42ECh. 5.2 - A CAT scan produces equally spaced cross-sectional...Ch. 5.2 - Prob. 44ECh. 5.2 - a If the region shown in the figure is rotated...Ch. 5.2 - a A model for the shape of a birds egg is obtained...Ch. 5.2 - Find the volume of the described solid S. A right...Ch. 5.2 - Find the volume of the described solid S. A...Ch. 5.2 - Find the volume of the described solid S. A cap of...Ch. 5.2 - Find the volume of the described solid S. A...Ch. 5.2 - Find the volume of the described solid S. A...Ch. 5.2 - Find the volume of the described solid S. A...Ch. 5.2 - Find the volume of described solid S. A...Ch. 5.2 - Find the volume of described solid S. The base of...Ch. 5.2 - Prob. 55ECh. 5.2 - Prob. 56ECh. 5.2 - Find the volume of the described solid S. The base...Ch. 5.2 - Prob. 58ECh. 5.2 - Prob. 59ECh. 5.2 - Find the volume of the described solid S. The base...Ch. 5.2 - Find the volume of the described solid S. The...Ch. 5.2 - Prob. 62ECh. 5.2 - a Set up an integral for the volume of a solid...Ch. 5.2 - Prob. 64ECh. 5.2 - Prob. 65ECh. 5.2 - Find the volume common to two circular cylinders,...Ch. 5.2 - Prob. 67ECh. 5.2 - A bowl is shaped like a hemisphere with diameter...Ch. 5.2 - Prob. 69ECh. 5.2 - Prob. 70ECh. 5.2 - Prob. 71ECh. 5.2 - Prob. 72ECh. 5.3 - Let S be the solid obtained by rotating the region...Ch. 5.3 - Let S be the solid obtained by rotating the region...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Let V be the volume of the solid obtained by...Ch. 5.3 - Prob. 9ECh. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Prob. 14ECh. 5.3 - Prob. 15ECh. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Use the method of cylindrical shells to find the...Ch. 5.3 - Prob. 20ECh. 5.3 - a Set up an integral for the volume of the solid...Ch. 5.3 - Prob. 22ECh. 5.3 - Prob. 23ECh. 5.3 - Prob. 24ECh. 5.3 - a Set up an integral for the volume of the solid...Ch. 5.3 - Prob. 26ECh. 5.3 - Prob. 27ECh. 5.3 - If the region shown in the figure is rotated about...Ch. 5.3 - Prob. 29ECh. 5.3 - Prob. 30ECh. 5.3 - Prob. 31ECh. 5.3 - Prob. 32ECh. 5.3 - Prob. 33ECh. 5.3 - Prob. 34ECh. 5.3 - Use a computer algebra system to find the exact...Ch. 5.3 - Prob. 36ECh. 5.3 - The region bounded by the given curves is rotated...Ch. 5.3 - The region bounded by the given curves is rotated...Ch. 5.3 - Prob. 39ECh. 5.3 - The region bounded by the given curves is rotated...Ch. 5.3 - The region bounded by the given curves is rotated...Ch. 5.3 - The region bounded by the given curves is rotated...Ch. 5.3 - The region bounded by the given curves is rotated...Ch. 5.3 - Let T be the triangular region with vertices...Ch. 5.3 - Prob. 45ECh. 5.3 - Prob. 46ECh. 5.3 - Prob. 47ECh. 5.3 - Suppose you make napkin rings by drilling holes...Ch. 5.4 - A 360-lb gorilla climbs a tree to a height of 20...Ch. 5.4 - Prob. 2ECh. 5.4 - Prob. 3ECh. 5.4 - Prob. 4ECh. 5.4 - Prob. 5ECh. 5.4 - The table shows values of a force function f(x)...Ch. 5.4 - A force of 10 lb is required to hold a spring...Ch. 5.4 - A spring has a natural length of 40 cm. If a 60-N...Ch. 5.4 - Suppose that 2 J of work is needed to stretch a...Ch. 5.4 - If the work required to stretch a spring 1 ft...Ch. 5.4 - A spring has natural length 20 cm. Compare the...Ch. 5.4 - Prob. 12ECh. 5.4 - Prob. 13ECh. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Prob. 17ECh. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Prob. 19ECh. 5.4 - Prob. 20ECh. 5.4 - Show how to approximate the required work by a...Ch. 5.4 - Prob. 22ECh. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - A tank is full of water. Find the work required to...Ch. 5.4 - Prob. 27ECh. 5.4 - Prob. 28ECh. 5.4 - Prob. 29ECh. 5.4 - In a steam engine the pressure P and volume V of...Ch. 5.4 - Prob. 31ECh. 5.4 - Prob. 32ECh. 5.4 - Prob. 33ECh. 5.4 - The Great Pyramid of King Khufu was built of...Ch. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 2ECh. 5.5 - Prob. 3ECh. 5.5 - Prob. 4ECh. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 6ECh. 5.5 - Find the average value of the function on the...Ch. 5.5 - Prob. 8ECh. 5.5 - a Find the average value of f on the given...Ch. 5.5 - Prob. 10ECh. 5.5 - a Find the average value of f on the given...Ch. 5.5 - a Find the average value of f on the given...Ch. 5.5 - If f is continuous and 13f(x)dx=8, show that f...Ch. 5.5 - Find the numbers b such that the average value of...Ch. 5.5 - Prob. 15ECh. 5.5 - The velocity graph of an accelerating car is...Ch. 5.5 - Prob. 17ECh. 5.5 - The velocity v of blood that flows in a blood...Ch. 5.5 - Prob. 19ECh. 5.5 - If a freely falling body starts from rest, then...Ch. 5.5 - Prob. 21ECh. 5.5 - Use the diagram to show that if f is concave...Ch. 5.5 - Prove that Mean value Theorem for Integrals by...Ch. 5.5 - Prob. 24ECh. 5.R - a Draw two typical curves y=f(x) and y=g(x) where...Ch. 5.R - Prob. 2CCCh. 5.R - a Suppose S is a solid with known cross-sectional...Ch. 5.R - a What is the volume of a cylindrical shell? b...Ch. 5.R - Suppose that you push a book across a 6-meter-long...Ch. 5.R - Prob. 6CCCh. 5.R - Prob. 1ECh. 5.R - Prob. 2ECh. 5.R - Prob. 3ECh. 5.R - Prob. 4ECh. 5.R - Prob. 5ECh. 5.R - Prob. 6ECh. 5.R - Prob. 7ECh. 5.R - Find the volume of the solid obtained by rotating...Ch. 5.R - Prob. 9ECh. 5.R - Prob. 10ECh. 5.R - Prob. 11ECh. 5.R - Set up, but do not evaluate, an integral for the...Ch. 5.R - Prob. 13ECh. 5.R - Prob. 14ECh. 5.R - Prob. 15ECh. 5.R - Let be the region in the first quadrant bounded...Ch. 5.R - Let be the region bounded by the curves...Ch. 5.R - Let be the region bounded by the curves y=1x2 and...Ch. 5.R - Prob. 19ECh. 5.R - Prob. 20ECh. 5.R - Prob. 21ECh. 5.R - Prob. 22ECh. 5.R - The base of a solid is a circular disk with radius...Ch. 5.R - The base of a solid is the region bounded by the...Ch. 5.R - The height of a monument is 20 m. A horizontal...Ch. 5.R - a The base of a solid is a square with vertices...Ch. 5.R - Prob. 27ECh. 5.R - Prob. 28ECh. 5.R - A tank full of water has the shape of a paraboloid...Ch. 5.R - A steel tank has the shape of a circular cylinder...Ch. 5.R - Prob. 31ECh. 5.R - Prob. 32ECh. 5.R - Prob. 33ECh. 5.R - Prob. 34ECh. 5.P - a Find a positive continuous function f such that...Ch. 5.P - There is a line through the origin that divides...Ch. 5.P - The figure shows a horizontal line y=c...Ch. 5.P - A cylindrical glass of radius r and height L is...Ch. 5.P - a Show that the volume of a segment of height h of...Ch. 5.P - Archimedes Principle states that the buoyant force...Ch. 5.P - Prob. 7PCh. 5.P - A sphere of radius 1 overlaps a smaller sphere of...Ch. 5.P - The figure shows a curve C with the property that,...Ch. 5.P - A paper drinking cup filled with water has the...Ch. 5.P - A clepsydra, or water clock, is a glass container...Ch. 5.P - A cylindrical container of radius r and height L...Ch. 5.P - Suppose the graph of a cubic polynomial intersects...Ch. 5.P - Suppose we are planning to make a taco from a...Ch. 5.P - Prob. 15P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Solve these exercises. Where necessary, round the answers to 2 decimal places unless otherwise specified. Find the volume of a prism with a base area of 125 square inches and a height of 8 inches.arrow_forwardSolve these exercises. Where necessary, round the answers to 2 decimal places unless otherwise specified. Find the volume of a prism that is 13.82 centimeters high and has an equilateral triangle base that has 9.08 centimeter sides. Round the answer to the nearest cubic centimeter.arrow_forwardSolve these prism and cylinder exercises. Where necessary, round the answers to 2 decimal places unless otherwise specified. Compute the volume of a prism with a base area of 220.0 square centimeters and a height of 7.600 centimeters.arrow_forward
Recommended textbooks for you
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Chain Rule dy:dx = dy:du*du:dx; Author: Robert Cappetta;https://www.youtube.com/watch?v=IUYniALwbHs;License: Standard YouTube License, CC-BY
CHAIN RULE Part 1; Author: Btech Maths Hub;https://www.youtube.com/watch?v=TIAw6AJ_5Po;License: Standard YouTube License, CC-BY