
Concept explainers
To determine the value of
Answer to Problem 5.123P
The value of
Explanation of Solution
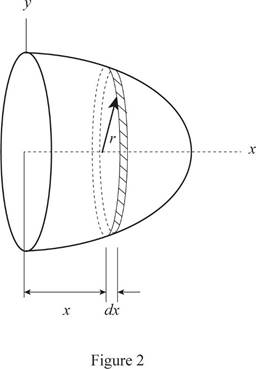
Refer Fig. P5.21 and Fig. 1.

Let the element of volume of the disk be of radius r and thickness dx.
Find the equation for radius from the equation of the generating curve.
Here, the y component is equal to the radius,
Write the expression for the volume of the element.
Find the centroid of the element.
Here,
Write the expression for the
Conclusion:
Refer Fig.2
Calculate the volume of component 1.
Calculate
Substitute
Thus, the value of
Calculate the volume of component 2.
Calculate
Substitute
Thus, the value of
Therefore, the value of
Want to see more full solutions like this?
Chapter 5 Solutions
Connect 1 Semester Access Card for Vector Mechanics for Engineers: Statics and Dynamics
- (i) The Area of Triangle (a1) in mm2 is (ii) The Area of circle (a2) in mm2 is (iii) x1 isarrow_forwardDetermine the following. Show the complete solution.arrow_forwardAn equilateral triangle of 35 mm side has an edge in the HP which is inclined at 40° to the VP. The plane itself is inclined at 50° to the HP. Draw the projections of this plane.arrow_forward
- Determine the value of the shaded area of the figure shown:arrow_forwardFind the volume of a right circular cylinder of radius a and height h if the density varies as the distance from the base. Note :- By Triple Integrals |arrow_forwardA quarter circle segment with a radius of 50 mm is extracted from the square plate. Calculate the coordinates of the geometric center of the resulting new shape.arrow_forward
- A ball of radius 5cm has a round hole of radius 3cm drilled through its center. Use Disk Method to find the exact volume of the resulting solid.arrow_forwardy THE FIGURE IS NOT DRAWN TO SCALE. The area shown is a (blue) solid semicircle with radius R = 6.6 in, and a (white) semicircular cutout (hole) with radius r = 3.6 in.arrow_forwardShow complete solutions. Draw the grapharrow_forward
- A vertical pole consists of two parts, each one half of the whole pole. At a point in the horizontal plane which passes through the foot of the pole and 36? from it, the upper half of the pole subtend an angle whose tangent is 1⁄3. How high is the pole?arrow_forwardwrite the answer. show the soluion #12arrow_forwardA windshield wiper rotates through a 120° angle as it cleans a windshield. From the point of rotation, the wiper blade begins at a distance of 4 in. and ends at a distance of 18 in. (The wiper blade is 14 in. in length.) Find the area cleaned by the wiper blade. 18"arrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
