
Mechanics of Materials (MindTap Course List)
9th Edition
ISBN: 9781337093347
Author: Barry J. Goodno, James M. Gere
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 7, Problem 7.5.4P
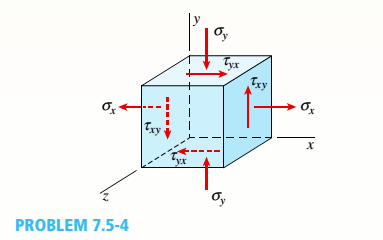
An element of a material is subjected to plane stresses as shown in the figure. The stresses o, cry., and are 10 MPa, —15 MPa, and 5 MPa. respectively. Assume E = 200 GPa and v = 0.3.
(a) Calculate the normal strain in the x, v. and z directions and the shear strain.
(b) Calculate the strain-energy density of the element.
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 7 Solutions
Mechanics of Materials (MindTap Course List)
Ch. 7 - An clement m plane stress from the frame of a...Ch. 7 - Solve the preceding problem for an element in...Ch. 7 - The stresses on an element are sx= 1000 Psi. sy=...Ch. 7 - .4 The stresses on an clement arc known to be sx=...Ch. 7 - The stresses acting on element A on the web of a...Ch. 7 - Solve the preceding problem if the stresses acting...Ch. 7 - The stresses acting on element B on the web of a...Ch. 7 - An element in plane stress on the fuselage of an...Ch. 7 - The stresses acting on element B (see figure part...Ch. 7 - Solve the preceding problem if the normal and...
Ch. 7 - The polyethylene liner of a settling pond is...Ch. 7 - Solve the preceding problem if the norm al and...Ch. 7 - Two steel rods are welded together (see figure):...Ch. 7 - Repeat the previous problem using ? = 50° and...Ch. 7 - A rectangular plate of dimensions 3.0 in. × 5.0...Ch. 7 - Solve the preceding problem for a plate of...Ch. 7 - A simply supported beam is subjected to point load...Ch. 7 - Repeat the previous problem using sx= 12 MPa.Ch. 7 - At a point on the surface of an elliptical...Ch. 7 - Solve the preceding problem for sx= 11 MPa and...Ch. 7 - An clement m plane stress from the frame of a...Ch. 7 - Solve the preceding problem for the element shown...Ch. 7 - : A gusset plate on a truss bridge is in plane...Ch. 7 - The surface of an airplane wing is subjected to...Ch. 7 - At a point on the web of a girder on an overhead...Ch. 7 - -26 A rectangular plate of dimensions 125 mm × 75...Ch. 7 - -27 A square plate with side dimension of 2 in. is...Ch. 7 - The stresses acting on an element are x= 750 psi,...Ch. 7 - Repeat the preceding problem using sx= 5.5 MPa....Ch. 7 - An element in plane stress is subjected to...Ch. 7 - -4. - An element in plane stress is subjected to...Ch. 7 - An element in plane stress is subjected to...Ch. 7 - The stresses acting on element A in the web of a...Ch. 7 - The normal and shear stresses acting on element A...Ch. 7 - An element in plane stress from the fuselage of an...Ch. 7 - -9The stresses acting on element B in the web of a...Ch. 7 - The normal and shear stresses acting on element B...Ch. 7 - ‘7.3-11 The stresses on an element are sx= -300...Ch. 7 - - 7.3-12 A simply supported beam is subjected to...Ch. 7 - A shear wall in a reinforced concrete building is...Ch. 7 - The state of stress on an element along the...Ch. 7 - -15 Repeat the preceding problem using ??. = - 750...Ch. 7 - A propeller shaft subjected to combined torsion...Ch. 7 - 3-17 The stresses at a point along a beam...Ch. 7 - -18 through 7.3-22 An element in plane stress (see...Ch. 7 - -18 through 7.3-22 An element in plane stress (see...Ch. 7 - -18 through 7.3-22 An element in plane stress (see...Ch. 7 - -18 through 7.3-22 An element in plane stress (see...Ch. 7 - -18 through 7.3-22 An element in plane stress (see...Ch. 7 - At a point on the web of a girder on a gantry...Ch. 7 - The stresses acting on a stress element on the arm...Ch. 7 - The stresses at a point on the down tube of a...Ch. 7 - An element in plane stress on the surface of an...Ch. 7 - A simply supported wood beam is subjected to point...Ch. 7 - A simply supported wood beam is subjected to point...Ch. 7 - Prob. 7.4.1PCh. 7 - .4-2 An element in uniaxial stress is subjected to...Ch. 7 - An element on the gusset plate in Problem 7.2-23...Ch. 7 - An element on the top surface of the fuel tanker...Ch. 7 - An element on the top surface of the fuel tanker...Ch. 7 - An element in biaxial stress is subjected to...Ch. 7 - • - 7.4-7 An element on the surface of a drive...Ch. 7 - - A specimen used in a coupon test has norm al...Ch. 7 - A specimen used in a coupon test is shown in the...Ch. 7 - The rotor shaft of a helicopter (see figure part...Ch. 7 - An element in pure shear is subjected to stresses...Ch. 7 - An clement in plane stress is subjected to...Ch. 7 - Prob. 7.4.13PCh. 7 - An clement in plane stress is subjected to...Ch. 7 - An clement in plane stress is subjected to...Ch. 7 - An clement in plane stress is subjected to...Ch. 7 - Prob. 7.4.17PCh. 7 - -18 through 7.4-25 An clement in plane stress is...Ch. 7 - -18 through 7.4-25 An clement in plane stress is...Ch. 7 - Prob. 7.4.20PCh. 7 - -18 through 7.4-25 An clement in plane stress is...Ch. 7 - Through 7.4-25 An clement in plane stress is...Ch. 7 - -18 through 7.4-25 An clement in plane stress is...Ch. 7 - through 7.4-25 An clement in plane stress is...Ch. 7 - -18 through 7.4-25 An clement in plane stress is...Ch. 7 - 1 A rectangular steel plate with thickness t = 5/8...Ch. 7 - Solve the preceding problem if the thickness of...Ch. 7 - The state of stress on an element of material is...Ch. 7 - An element of a material is subjected to plane...Ch. 7 - Assume that the normal strains x and y , for an...Ch. 7 - A cast-iron plate in biaxial stress is subjected...Ch. 7 - Solve the preceding problem for a steel plate with...Ch. 7 - • - 3 A rectangular plate in biaxial stress (see...Ch. 7 - Solve the preceding problem for an aluminum plate...Ch. 7 - A brass cube of 48 mm on each edge is comp ressed...Ch. 7 - 7.5-11 in. cube of concrete (E = 4.5 X 106 psi. v...Ch. 7 - -12 A square plate of a width h and thickness t is...Ch. 7 - Solve the preceding problem for an aluminum plate...Ch. 7 - A circle of a diameter d = 200 mm is etched on a...Ch. 7 - The normal stress on an elastomeric rubber pad in...Ch. 7 - A rubber sheet in biaxial stress is subjected to...Ch. 7 - An element of aluminum is subjected to tri-axial...Ch. 7 - An element of aluminum is subjected to tri- axial...Ch. 7 - -3 An element of aluminum in the form of a...Ch. 7 - Solve the preceding problem if the element is...Ch. 7 - A cube of cast iron with sides of length a = 4.0...Ch. 7 - Solve the preceding problem if the cube is granite...Ch. 7 - An element of aluminum is subjected to iriaxial...Ch. 7 - Prob. 7.6.8PCh. 7 - A rubber cylinder R of length L and cross-...Ch. 7 - A block R of rubber is confined between plane...Ch. 7 - -11 A rubber cube R of a side L = 3 in. and cross-...Ch. 7 - A copper bar with a square cross section is...Ch. 7 - A solid spherical ball of magnesium alloy (E = 6.5...Ch. 7 - A solid steel sphere (E = 210 GPa, v = 0.3) is...Ch. 7 - Prob. 7.6.15PCh. 7 - An element of material in plain strain has the...Ch. 7 - An clement of material in plain strain has the...Ch. 7 - An element of material in plain strain is...Ch. 7 - An element of material in plain strain is...Ch. 7 - A thin rectangular plate in biaxial stress is...Ch. 7 - Prob. 7.7.6PCh. 7 - A thin square plate in biaxial stress is subjected...Ch. 7 - Prob. 7.7.8PCh. 7 - An clement of material subjected to plane strain...Ch. 7 - Solve the preceding problem for the following...Ch. 7 - The strains for an element of material in plane...Ch. 7 - Solve the preceding problem for the following...Ch. 7 - An clement of material in plane strain (see...Ch. 7 - Solve the preceding problem for the following...Ch. 7 - A brass plate with a modulus of elastici ty E = 16...Ch. 7 - Solve the preceding problem if the plate is made...Ch. 7 - An element in plane stress is subjected to...Ch. 7 - Prob. 7.7.18PCh. 7 - During a test of an airplane wing, the strain gage...Ch. 7 - A strain rosette (see figure) mounted on the...Ch. 7 - A solid circular bar with a diameter of d = 1.25...Ch. 7 - A cantilever beam with a rectangular cross section...Ch. 7 - Solve the preceding problem if the cross-...Ch. 7 - A 600 strain rosette, or delta rosette, consists...Ch. 7 - On the surface of a structural component in a...Ch. 7 - - 7.2-26 The strains on the surface of an...Ch. 7 - Solve Problem 7.7-9 by using Mohr’s circle for...Ch. 7 - 7.7-28 Solve Problem 7.7-10 by using Mohr’s circle...Ch. 7 - Solve Problem 7.7-11 by using Mohr’s circle for...Ch. 7 - Solve Problem 7.7-12 by using Mohr’s circle for...Ch. 7 - Solve Problem 7.7-13 by using Mohr’s circle for...Ch. 7 - Prob. 7.7.32P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, mechanical-engineering and related others by exploring similar questions and additional content below.Similar questions
- • - 3 A rectangular plate in biaxial stress (see figure) is subjected to normal stresses u = 67 MPa (tension) and s = -23 MPa (compression). The plate has dimensions 400 X 550 X 20 mm and is made of steel with E = 200 GPa and v = 0.30. (a) Determine the maximum in-plane shear strain ?max in the plate. (b) Determine the change ?t in the thickness of the plate. (c) Determine the change ?t in the volume of the plate.arrow_forward-18 through 7.3-22 An element in plane stress (see figure) is subjected to stresses o, a., and (a) Determine the principal stresses and show them on a sketch of a properly oriented element. (b) Determine the maximum shear stresses and associated normal stresses and show them on a sketch of a properly oriented element. 7.3-18 a=2I50kPa, ay=375kPa.Txy.=-460kPaarrow_forwardThe strains for an element of material in plane strain (see figure) are as follows: x = 480 ×10-6. y = 140 × l0-6, and xy = —350 x 10”. Determine the principals strains and maximum shear strains, and show these strains on sketches of properly oriented elements.arrow_forward
- Plastic bar of diameter d = 32 mm is compressed in a testing device by a Force P = 190 N that is applied as shown in the figure. (a) Determine the normal and shear stresses acting: on all faces of stress elements oriented at (1 ) an angle 8 = 00, (2) an angle ?? = 22.5s, and (3) an angle ?? = 45°. In each case, show the stresses on a sketch of a properly oriented element. What are smaxtmax (b) Find smax and tmax in the plastic bar if a re-cantering spring of stiffness k is inserted into the testing device, as shown in the figure. The spring stillness is 1/6 of the axial stiffness of the plastic bar.arrow_forward-11 A solid steel bar (G = 11.8 X 106 psi ) of diameter d = 2,0 in. is subjected to torques T = 8.0 kip-in. acting in the directions shown in the figure. Determine the maximum shear, tensile, and compressive stresses in the bar and show these stresses on sketches of properly oriented stress elements. Determine the corresponding maximum strains (shear, tensile, and compressive) in the bar and show these strains on sketches of the deformed elements.arrow_forwardThe normal strain in the 45n direction on the surface of a circular tube (sec figure) is 880 × 10 when the torque T = 750 lb-in. The tube is made of copper alloy with G = 6.2 × 106 psi and y = 0.35. If the outside diameter d2of the tube is 0.8 in., what is the inside diameter dt? If the allowable normal stress in the tube is 14 ksi, what is the maximum permissible inside diameter d?arrow_forward
- A slightly tapered bar AB of rectangular cross section and length L is acted upon by a force P (see figure). The width of the bar varies uniformly From b2at end A to b1at end B. The thickness t is constant. (a) Determine the strain energy U of the bar. (b) Determine the elongation ?? of the bar by equating the strain energy to the work done by the force P.arrow_forward7.5-11 in. cube of concrete (E = 4.5 X 106 psi. v = 0.2) is compressed in biaxial stress by means of a framework that is loaded as shown in the figure. Assuming that each load F equals 25 kips. determine the change iv in the volume of the cube and the strain energy U stored in the cube.arrow_forward-7 The truss A BC Shawn in the figure supports a horizontal load P1= 300 lb and a vertical load P2= 9001b. Both bars have a cross-sectional area A = 2.4 in2 and are made of steel with E = 30 X 106 psi. (a) Determine the strain energy U1of the truss when the load P1acts alone (P2= 0). (b) Determine the strain energy U2when the load P2acts alone (P1= 0). (c) Determine the strain energy U3when both loads act simultaneously.arrow_forward
- An element in plane stress is subjected to stresses ?? = -8400 psi, ??y = 1100 psi, and (see figure). The material is aluminum with modulus of elasticity E = 10,000 ksi and Poisson’s ratio v = 0.33. Determine the following quantities: (a) the strains for an element oriented at an angle 0 = 30°, (b) the principal strains, and (C) the maximum shear strains. Show the results on sketches of properly oriented elements.arrow_forwardA copper bar with a rectangular cross section is held without stress between rigid supports (see figure). Subsequently, the temperature of the bar is raised 50°C (a) Determine the stresses on all faces of the elements A and B, and show these stresses on sketches of the elements. (Assume = 17.5 × 10-6/? and E = 120 GPa ) (b) If the shear stress at B is known to be 48 MPa at some inclination 8, find anglearrow_forwardAn element of aluminum is subjected to iriaxial stress (see figure). (a) Find the bulk modulus A^for the aluminum if the following stress and strain data are known: normal stresses are v = 5200 psi (tension), a = —4750 psi (compression); and (7_ = —3090 psi (compression) and normal strains in the v and v directions areet = 713,8 X 10_ (elongation) and £y=-502.3 x 10~6 (shortening), (b) If the element is replaced by one of magnesium, find the modulus of elasticity E and Poisson's ratio eif the following data is given: bulk modulus A' = 6,8 x 10 psi; normal stresses are trx= 4550 psi (tension), o", = —1700 psi (compression), and ex= 900 X 10"6 (elongation),arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning
Mechanics of Materials (MindTap Course List)Mechanical EngineeringISBN:9781337093347Author:Barry J. Goodno, James M. GerePublisher:Cengage Learning

Mechanics of Materials (MindTap Course List)
Mechanical Engineering
ISBN:9781337093347
Author:Barry J. Goodno, James M. Gere
Publisher:Cengage Learning
Lec21, Part 5, Strain transformation; Author: Mechanics of Materials (Libre);https://www.youtube.com/watch?v=sgJvz5j_ubM;License: Standard Youtube License