Calculus: An Applied Approach (MindTap Course List)
10th Edition
ISBN: 9781305860919
Author: Ron Larson
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 7.6, Problem 44E
HOW DO YOU SEE IT? The graphs show the constraint and several level curves of the objective function. Use the graph to approximate the indicated extrema.
(a) Maximize z = xy
Constraint:
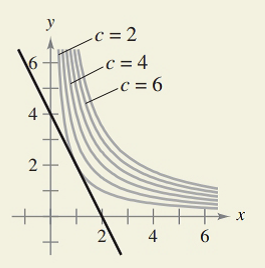
(b) Minimize
Constraint:
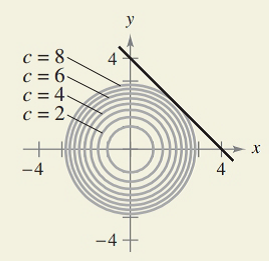
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
Write a resource constraint for this situation: A lawn service company has 40 hours of worker time available. Mowing a lawn (x) takes three hours and trimming (y) takes two hours. The profit from mowing is $15 and the profit from trimming is $10.
August eats a mix of Food X and Food Y for lunch. The amount of protein, calories,and sodium per ounce for each is shown in the table below. August’s lunch should provide atleast 520 calories but less than or equal to 750 milligrams of sodium. August would like to maximize the amount of protein in his lunch mix.Let x denote the number of ounces for Food X and let y denote the number of ounces of Food Y.
Topic: Graphical Methods
please help me out
Chapter 7 Solutions
Calculus: An Applied Approach (MindTap Course List)
Ch. 7.1 - Plot the points in the same three-dimensional...Ch. 7.1 - Prob. 2CPCh. 7.1 - Prob. 3CPCh. 7.1 - Find the standard equation of the sphere with...Ch. 7.1 - Prob. 5CPCh. 7.1 - Prob. 6CPCh. 7.1 - Prob. 7CPCh. 7.1 - Prob. 1SWUCh. 7.1 - Prob. 2SWUCh. 7.1 - Prob. 3SWU
Ch. 7.1 - Prob. 4SWUCh. 7.1 - Prob. 5SWUCh. 7.1 - Prob. 6SWUCh. 7.1 - Prob. 7SWUCh. 7.1 - Prob. 8SWUCh. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Finding the Coordinates of a Point in Space In...Ch. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10ECh. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Finding the Distance Between Two Points in Space...Ch. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.2 - Find the x-, y-, and z-intercepts of the plane...Ch. 7.2 - Prob. 2CPCh. 7.2 - Prob. 3CPCh. 7.2 - Prob. 1SWUCh. 7.2 - Prob. 2SWUCh. 7.2 - Prob. 3SWUCh. 7.2 - Prob. 4SWUCh. 7.2 - Prob. 5SWUCh. 7.2 - In Exercises 5 and 6, write the equation of the...Ch. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Matching In Exercises 23-28, match the equation...Ch. 7.2 - Classifying a Quadric Surface In Exercises 35-48,...Ch. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Physical Science Because of the forces caused by...Ch. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.3 - Prob. 1CPCh. 7.3 - Consider the function f(x,y)=9x2y2 a. Find the...Ch. 7.3 - Prob. 3CPCh. 7.3 - Prob. 4CPCh. 7.3 - Prob. 5CPCh. 7.3 - Prob. 1SWUCh. 7.3 - Prob. 2SWUCh. 7.3 - Prob. 3SWUCh. 7.3 - Prob. 4SWUCh. 7.3 - Prob. 5SWUCh. 7.3 - Prob. 6SWUCh. 7.3 - Prob. 7SWUCh. 7.3 - Prob. 8SWUCh. 7.3 - Prob. 9SWUCh. 7.3 - Prob. 10SWUCh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Evaluating Functions of Several Variables In...Ch. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Finding the Domain and Range of a Function In...Ch. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Matching In Exercises 31-34, match the graph of...Ch. 7.3 - Prob. 32ECh. 7.3 - Matching In Exercises 31-34, match the graph of...Ch. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.4 - Prob. 1CPCh. 7.4 - Prob. 2CPCh. 7.4 - Prob. 3CPCh. 7.4 - Prob. 4CPCh. 7.4 - Prob. 5CPCh. 7.4 - Prob. 6CPCh. 7.4 - Prob. 7CPCh. 7.4 - Prob. 1SWUCh. 7.4 - Prob. 2SWUCh. 7.4 - Prob. 3SWUCh. 7.4 - Prob. 4SWUCh. 7.4 - Prob. 5SWUCh. 7.4 - Prob. 6SWUCh. 7.4 - Prob. 7SWUCh. 7.4 - Prob. 8SWUCh. 7.4 - Prob. 9SWUCh. 7.4 - Prob. 10SWUCh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7.4 - Prob. 53ECh. 7.4 - Prob. 54ECh. 7.4 - Prob. 55ECh. 7.4 - Prob. 56ECh. 7.4 - Prob. 57ECh. 7.4 - Prob. 58ECh. 7.4 - Prob. 59ECh. 7.4 - Finding Second Partial Derivatives In Exercises...Ch. 7.4 - Marginal Cost A company manufactures mountain...Ch. 7.4 - Prob. 62ECh. 7.4 - Prob. 63ECh. 7.4 - Prob. 64ECh. 7.4 - Prob. 65ECh. 7.4 - Prob. 66ECh. 7.4 - Prob. 67ECh. 7.4 - Prob. 68ECh. 7.4 - Prob. 69ECh. 7.4 - Investment The value of an investment of $ 100...Ch. 7.4 - Prob. 72ECh. 7.4 - Prob. 73ECh. 7.5 - Prob. 1CPCh. 7.5 - Prob. 2CPCh. 7.5 - Find the relative extrema and saddle points of...Ch. 7.5 - Prob. 4CPCh. 7.5 - Prob. 5CPCh. 7.5 - Prob. 1SWUCh. 7.5 - Prob. 2SWUCh. 7.5 - Prob. 3SWUCh. 7.5 - Prob. 4SWUCh. 7.5 - Prob. 5SWUCh. 7.5 - Prob. 6SWUCh. 7.5 - Prob. 7SWUCh. 7.5 - Prob. 8SWUCh. 7.5 - Prob. 9SWUCh. 7.5 - Prob. 10SWUCh. 7.5 - Prob. 11SWUCh. 7.5 - Prob. 12SWUCh. 7.5 - Prob. 13SWUCh. 7.5 - Prob. 14SWUCh. 7.5 - Prob. 1ECh. 7.5 - Prob. 2ECh. 7.5 - Prob. 3ECh. 7.5 - Prob. 4ECh. 7.5 - Prob. 5ECh. 7.5 - Prob. 6ECh. 7.5 - Prob. 7ECh. 7.5 - Prob. 8ECh. 7.5 - Prob. 9ECh. 7.5 - Prob. 10ECh. 7.5 - Prob. 11ECh. 7.5 - Prob. 12ECh. 7.5 - Prob. 13ECh. 7.5 - Prob. 14ECh. 7.5 - Prob. 15ECh. 7.5 - Prob. 16ECh. 7.5 - Prob. 17ECh. 7.5 - Prob. 18ECh. 7.5 - Prob. 19ECh. 7.5 - Prob. 20ECh. 7.5 - Prob. 21ECh. 7.5 - Prob. 22ECh. 7.5 - Prob. 23ECh. 7.5 - Prob. 24ECh. 7.5 - Prob. 25ECh. 7.5 - Prob. 26ECh. 7.5 - Prob. 27ECh. 7.5 - Prob. 28ECh. 7.5 - Prob. 29ECh. 7.5 - Prob. 30ECh. 7.5 - Prob. 31ECh. 7.5 - Prob. 32ECh. 7.5 - Prob. 33ECh. 7.5 - Prob. 34ECh. 7.5 - Prob. 35ECh. 7.5 - Prob. 36ECh. 7.5 - Revenue A company manufactures running shoes and...Ch. 7.5 - Revenue A retail outlet sells two types of riding...Ch. 7.5 - Prob. 39ECh. 7.5 - Prob. 40ECh. 7.5 - Prob. 41ECh. 7.5 - Profit A corporation manufactures candles at two...Ch. 7.5 - Prob. 43ECh. 7.5 - Finding a Maximum Volume In Exercises 43 and 44,...Ch. 7.5 - Volume Find the dimensions of a rectangular...Ch. 7.5 - Prob. 46ECh. 7.5 - Cost A manufacturer makes an open-top wooden crate...Ch. 7.5 - Cost A home improvement contractor is painting the...Ch. 7.5 - Cost An automobile manufacturer has determined...Ch. 7.5 - Prob. 50ECh. 7.5 - Biology A lake is to be stocked with smallmouth...Ch. 7.5 - Prob. 53ECh. 7.5 - Shannon Diversity Index One way to measure species...Ch. 7.5 - Prob. 55ECh. 7.5 - Prob. 56ECh. 7.5 - Prob. 1QYCh. 7.5 - Prob. 2QYCh. 7.5 - Prob. 3QYCh. 7.5 - Prob. 4QYCh. 7.5 - Prob. 5QYCh. 7.5 - Prob. 6QYCh. 7.5 - Prob. 7QYCh. 7.5 - Prob. 8QYCh. 7.5 - Prob. 9QYCh. 7.5 - Prob. 10QYCh. 7.5 - Prob. 11QYCh. 7.5 - Prob. 12QYCh. 7.5 - Prob. 13QYCh. 7.5 - Prob. 14QYCh. 7.5 - Prob. 15QYCh. 7.5 - Prob. 16QYCh. 7.5 - Prob. 17QYCh. 7.5 - Prob. 18QYCh. 7.5 - Prob. 19QYCh. 7.5 - Prob. 20QYCh. 7.5 - Prob. 21QYCh. 7.5 - Prob. 22QYCh. 7.5 - Prob. 23QYCh. 7.5 - Prob. 24QYCh. 7.5 - Prob. 25QYCh. 7.5 - Prob. 26QYCh. 7.6 - Find the maximum volume of V=xyz subject to the...Ch. 7.6 - Prob. 2CPCh. 7.6 - Prob. 3CPCh. 7.6 - Prob. 4CPCh. 7.6 - Prob. 1SWUCh. 7.6 - Prob. 2SWUCh. 7.6 - Prob. 3SWUCh. 7.6 - Prob. 4SWUCh. 7.6 - Prob. 5SWUCh. 7.6 - Prob. 6SWUCh. 7.6 - Prob. 7SWUCh. 7.6 - Prob. 8SWUCh. 7.6 - Prob. 9SWUCh. 7.6 - Prob. 10SWUCh. 7.6 - Prob. 1ECh. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - Prob. 4ECh. 7.6 - Prob. 5ECh. 7.6 - Prob. 6ECh. 7.6 - Prob. 7ECh. 7.6 - Prob. 8ECh. 7.6 - Prob. 9ECh. 7.6 - Using Lagrange Multipliers In Exercises 1-12, use...Ch. 7.6 - Prob. 11ECh. 7.6 - Prob. 12ECh. 7.6 - Prob. 13ECh. 7.6 - Prob. 14ECh. 7.6 - Prob. 15ECh. 7.6 - Prob. 16ECh. 7.6 - Prob. 17ECh. 7.6 - Prob. 18ECh. 7.6 - Prob. 19ECh. 7.6 - Prob. 20ECh. 7.6 - Prob. 21ECh. 7.6 - Prob. 22ECh. 7.6 - Prob. 23ECh. 7.6 - Prob. 24ECh. 7.6 - Prob. 25ECh. 7.6 - Prob. 26ECh. 7.6 - Finding Distance In Exercises 23-28, find the...Ch. 7.6 - Prob. 28ECh. 7.6 - Volume A rectangular box is resting on the...Ch. 7.6 - Prob. 30ECh. 7.6 - Cost In redecorating an office, the cost for new...Ch. 7.6 - Cost A cargo container (in the shape of a...Ch. 7.6 - Cost A manufacturer has an order for 1000 units of...Ch. 7.6 - Prob. 34ECh. 7.6 - Prob. 35ECh. 7.6 - Prob. 36ECh. 7.6 - Prob. 37ECh. 7.6 - Least-Cost Rule Repeat Exercise 37 for the...Ch. 7.6 - Construction An animal shelter plans to use the...Ch. 7.6 - Office Space Partitions will be used in an office...Ch. 7.6 - Biology A microbiologist must prepare a culture...Ch. 7.6 - Prob. 42ECh. 7.6 - Nutrition The number of grams of your favorite ice...Ch. 7.6 - HOW DO YOU SEE IT? The graphs show the constraint...Ch. 7.6 - Prob. 45ECh. 7.7 - Prob. 1CPCh. 7.7 - Prob. 2CPCh. 7.7 - Prob. 3CPCh. 7.7 - Prob. 1SWUCh. 7.7 - Prob. 2SWUCh. 7.7 - Prob. 3SWUCh. 7.7 - Prob. 4SWUCh. 7.7 - Prob. 5SWUCh. 7.7 - Prob. 6SWUCh. 7.7 - Prob. 7SWUCh. 7.7 - Prob. 8SWUCh. 7.7 - Prob. 1ECh. 7.7 - Prob. 2ECh. 7.7 - Prob. 3ECh. 7.7 - Prob. 4ECh. 7.7 - Prob. 5ECh. 7.7 - Prob. 6ECh. 7.7 - Prob. 7ECh. 7.7 - Prob. 8ECh. 7.7 - Prob. 9ECh. 7.7 - Prob. 10ECh. 7.7 - Prob. 11ECh. 7.7 - Prob. 12ECh. 7.7 - Prob. 13ECh. 7.7 - Prob. 14ECh. 7.7 - Prob. 15ECh. 7.7 - Demand A hardware retailer wants to know the...Ch. 7.7 - Prob. 17ECh. 7.7 - HOW DO YOU SEE IT? Match the regression equation...Ch. 7.7 - Prob. 19ECh. 7.7 - Prob. 20ECh. 7.7 - Prob. 21ECh. 7.7 - Prob. 22ECh. 7.7 - Prob. 23ECh. 7.7 - Prob. 24ECh. 7.7 - Prob. 25ECh. 7.7 - Prob. 26ECh. 7.7 - Prob. 27ECh. 7.7 - Prob. 28ECh. 7.7 - Prob. 29ECh. 7.7 - Prob. 30ECh. 7.8 - Prob. 1CPCh. 7.8 - Prob. 2CPCh. 7.8 - Prob. 3CPCh. 7.8 - Prob. 4CPCh. 7.8 - Prob. 5CPCh. 7.8 - Prob. 6CPCh. 7.8 - Prob. 1SWUCh. 7.8 - Prob. 2SWUCh. 7.8 - Prob. 3SWUCh. 7.8 - Prob. 4SWUCh. 7.8 - Prob. 5SWUCh. 7.8 - Prob. 6SWUCh. 7.8 - Prob. 7SWUCh. 7.8 - Prob. 8SWUCh. 7.8 - Prob. 9SWUCh. 7.8 - Prob. 10SWUCh. 7.8 - Prob. 11SWUCh. 7.8 - Prob. 12SWUCh. 7.8 - Prob. 13SWUCh. 7.8 - Prob. 14SWUCh. 7.8 - Prob. 15SWUCh. 7.8 - Prob. 16SWUCh. 7.8 - Prob. 1ECh. 7.8 - Finding Partial Integrals In Exercises 1-10, find...Ch. 7.8 - Prob. 3ECh. 7.8 - Prob. 4ECh. 7.8 - Prob. 5ECh. 7.8 - Prob. 6ECh. 7.8 - Prob. 7ECh. 7.8 - Prob. 8ECh. 7.8 - Prob. 9ECh. 7.8 - Prob. 10ECh. 7.8 - Prob. 11ECh. 7.8 - Prob. 12ECh. 7.8 - Prob. 13ECh. 7.8 - Prob. 14ECh. 7.8 - Prob. 15ECh. 7.8 - Prob. 16ECh. 7.8 - Evaluating a Double Integral In Exercises 11-24,...Ch. 7.8 - Prob. 18ECh. 7.8 - Prob. 19ECh. 7.8 - Prob. 20ECh. 7.8 - Prob. 21ECh. 7.8 - Prob. 22ECh. 7.8 - Prob. 23ECh. 7.8 - Prob. 24ECh. 7.8 - Prob. 25ECh. 7.8 - Finding Area with a Double Integral In Exercises...Ch. 7.8 - Prob. 27ECh. 7.8 - Prob. 28ECh. 7.8 - Finding Area with a Double Integral In Exercises...Ch. 7.8 - Prob. 30ECh. 7.8 - Prob. 31ECh. 7.8 - Prob. 32ECh. 7.8 - Prob. 33ECh. 7.8 - Prob. 34ECh. 7.8 - Prob. 35ECh. 7.8 - Finding Area with a Double Integral In Exercises...Ch. 7.8 - Prob. 37ECh. 7.8 - Prob. 38ECh. 7.8 - Changing the Order of Integration In Exercises...Ch. 7.8 - Prob. 40ECh. 7.8 - Prob. 41ECh. 7.8 - Prob. 42ECh. 7.8 - Changing the Order of Integration In Exercises...Ch. 7.8 - Prob. 44ECh. 7.8 - Prob. 45ECh. 7.8 - Prob. 46ECh. 7.8 - Prob. 47ECh. 7.8 - Prob. 48ECh. 7.8 - Think About It Explain why you need to change the...Ch. 7.8 - Prob. 50ECh. 7.8 - Prob. 51ECh. 7.8 - Prob. 52ECh. 7.8 - Prob. 53ECh. 7.8 - Prob. 54ECh. 7.8 - Prob. 55ECh. 7.8 - Prob. 56ECh. 7.8 - Prob. 57ECh. 7.8 - Prob. 58ECh. 7.8 - Prob. 59ECh. 7.8 - Prob. 60ECh. 7.9 - Find the volume of the solid region hounded in the...Ch. 7.9 - Prob. 2CPCh. 7.9 - Prob. 3CPCh. 7.9 - Prob. 4CPCh. 7.9 - Prob. 5CPCh. 7.9 - Prob. 1SWUCh. 7.9 - Prob. 2SWUCh. 7.9 - Prob. 3SWUCh. 7.9 - Prob. 4SWUCh. 7.9 - Prob. 5SWUCh. 7.9 - Prob. 6SWUCh. 7.9 - Prob. 7SWUCh. 7.9 - Prob. 8SWUCh. 7.9 - Prob. 9SWUCh. 7.9 - Prob. 10SWUCh. 7.9 - Prob. 1ECh. 7.9 - Prob. 2ECh. 7.9 - Prob. 3ECh. 7.9 - Finding the Volume of a Solid Region In Exercises...Ch. 7.9 - Prob. 5ECh. 7.9 - Prob. 6ECh. 7.9 - Prob. 7ECh. 7.9 - Prob. 8ECh. 7.9 - Prob. 9ECh. 7.9 - Prob. 10ECh. 7.9 - Prob. 11ECh. 7.9 - Prob. 12ECh. 7.9 - Prob. 13ECh. 7.9 - Prob. 14ECh. 7.9 - Finding the Volume of a Solid Region In Exercises...Ch. 7.9 - Prob. 16ECh. 7.9 - Prob. 17ECh. 7.9 - Finding the Volume of a Solid Region In Exercises...Ch. 7.9 - Prob. 19ECh. 7.9 - Prob. 20ECh. 7.9 - Prob. 21ECh. 7.9 - Prob. 22ECh. 7.9 - Prob. 23ECh. 7.9 - Prob. 24ECh. 7.9 - Prob. 25ECh. 7.9 - Population Density The population density (in...Ch. 7.9 - Prob. 27ECh. 7.9 - Prob. 28ECh. 7.9 - Prob. 29ECh. 7.9 - Prob. 30ECh. 7.9 - Average Weekly Profit A firms weekly profit P (in...Ch. 7.9 - Prob. 32ECh. 7.9 - Prob. 33ECh. 7.9 - Prob. 34ECh. 7.9 - Prob. 35ECh. 7.9 - Prob. 36ECh. 7 - Plotting Points in Space In Exercises 1 and 2,...Ch. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Finding a Trace of a Sphere In Exercises 13 and...Ch. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RECh. 7 - Prob. 82RECh. 7 - Prob. 83RECh. 7 - Prob. 84RECh. 7 - Prob. 85RECh. 7 - Prob. 86RECh. 7 - Evaluating a Double Integral In Exercises 85-88,...Ch. 7 - Prob. 88RECh. 7 - Prob. 89RECh. 7 - Prob. 90RECh. 7 - Finding Area with a Double Integral In Exercises...Ch. 7 - Finding Area with a Double Integral In Exercises...Ch. 7 - Finding the Volume of a Solid Region In Exercises...Ch. 7 - Prob. 94RECh. 7 - Prob. 95RECh. 7 - Prob. 96RECh. 7 - Prob. 97RECh. 7 - Prob. 98RECh. 7 - Prob. 99RECh. 7 - Prob. 100RECh. 7 - Prob. 101RECh. 7 - Average Revenue A company sells two products whose...Ch. 7 - Prob. 103RECh. 7 - Average Production Repeat Exercise 103 for the...Ch. 7 - Prob. 1TYSCh. 7 - Prob. 2TYSCh. 7 - Prob. 3TYSCh. 7 - Prob. 4TYSCh. 7 - Prob. 5TYSCh. 7 - Prob. 6TYSCh. 7 - Prob. 7TYSCh. 7 - Prob. 8TYSCh. 7 - Prob. 9TYSCh. 7 - Prob. 10TYSCh. 7 - Prob. 11TYSCh. 7 - Prob. 12TYSCh. 7 - Prob. 13TYSCh. 7 - Prob. 14TYSCh. 7 - Prob. 15TYSCh. 7 - Prob. 16TYSCh. 7 - Prob. 17TYSCh. 7 - Prob. 18TYSCh. 7 - Prob. 19TYSCh. 7 - Prob. 20TYSCh. 7 - Prob. 21TYSCh. 7 - Prob. 22TYS
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Use your schools library, the Internet, or some other reference source to find the real-life applications of constrained optimization.arrow_forwardA company manufactures two fertilizers, x and y. Each 50-pound bag of fertilizer requires three ingredients, which are available in the limited quantities shown in the table. The profit on each bag of fertilizer x is 6 and on each bag of y is 5. How many bags of each product should be produced to maximize the profit? Ingredient Number of Pounds in Fertilizer x Number of Pounds in Fertilizer y Total number of Pounds Available Nitrogen 6 10 20,000 Phosphorus 8 6 16,400 Potash 6 4 12,000arrow_forwardFind the maximum value of P=4x+3y subject to the constraints of Example 1. {x+y42x+y6x0y0arrow_forward
- In Example 5, the candy manufacturer improves the production of chocolate-covered creams so that the profit is $2.50 per box. The constraints do not change. What is the maximum monthly profit? How many boxes of each type are produced per month to yield the maximum profit?arrow_forwardThe manufacturer of a weight training bench spends $120 to build each bench and sells them for $170. The manufacturer also has fixed costs each month of $150,000. (a) Find the cost function C when x benches are manufactured. (b) Find the revenue function R when x benches are sold. (c) Show the break-even point by graphing both the Revenue and Cost functions on the same grid. (d) Find the break-even point. Interpret what the break-even point means.arrow_forwardCompare and contrast the graphs of y=x2 and y=2x.arrow_forward
- The manufacturer of an energy drink spends $1.20 to make each drink and sells them for $2. The manufacturer also has fixed costs each month of $8,000. (a) Find the cost function C when x energy drinks aremanufactured. (b) Find the revenue function R when x drinks are sold. (c) Show the break-even point by graphing both the Revenue and Cost functions on the same grid. (d) Find the break-even point. Interpret what the breakeven point means.arrow_forwardMary needs to purchase supplies of answer sheets and pencils for a standardized test to be given to the juniors at her high school. The number of the answer sheets needed is at least 5 more than twice the number of pencils. The pencils cost $2 and the answer sheets cost $1. Mary’s budget for these supplies allows for a maximum cost of $400. (a) Write a system of inequalities to model this situation. (b) Graph the system. (c) Could Mary purchase 100 pencils and 100 answer sheets? (d) Could Mary purchase 150 pencils and 150 answer sheets?arrow_forwardA trailer can carry a maximum weight of 160 pounds and a maximum volume of 15 cubic feet. A microwave oven weighs 30 pounds and has 2 cubic feet of volume, while a printer weighs 20 pounds and has 3 cubic feet of space. (a) Write a system of inequalities to model this situation. (b) Graph the system. (c) Could 4 microwaves and 2 printers be carried on this trailer? (d) Could 7 microwaves and 3 printers be carried on this trailer?arrow_forward
- A company produces two types of drills, a cordless model and a corded model. The cordless model requires 3 hours, and the corded-type drill requires 1 hours to make. The company has 180 work hours per day for manufacturing. The factory has space for storage of 140 drills per day. Let z = the number of cordless drills produced per day and y = the number of corded drills produced per day. Write the system of inequalities for these constraints: Assembly: 3x + y Storage: x+y 250+ 240 230- 220- 210- 200 Graph the feasible region for this system of inequalities. Note: To get the correct feasible region, you need to also include the non-negative constraints on your graph (≥0 and y ≥ 0). These will give you boundary lines on the x-axis and y-axis. 190 180 170- 160- 150 140 130 120 110- 100 90- 688888888 80 70 60- 50- 40- 30 20- 10 <180 <140 Clear All Draw: 10 20 30 40 50 60 70 80 90 100 110 120 130 140 150 160 170 180 190 200 210 220 230 240 250arrow_forwardRead the information below and construct the objective function, and the associated constraint inequalities. DO NOT SOLVE THE MINIMUM PROBLEM. The liquid portion of a diet is to provide at least 380 calories, at least 80 units of vitamin A, and at least 140 units of vitamin C daily. A cup of dietary drink X provides 50 calories, 20 units of vitamin A, and 30 units of vitamin C. A cup of dietary drink Y provides 40 calories, 30 units of vitamin A, and 90 units of vitamin C. Dietary drink X costs $0.24 per cup and drink Y costs $0.31 per cup. Construct the objective function for minimizing the cost, and construct the associated constraint inequalities to meet the daily dietary requirements by selecting the appropriate symbol or number from the dropdown list. Note: The symbol = in the dropdown list indicates "greater than or equal to". Cost = [Select] [Select] 20X+ [Select] [Select] X+ [Select ] X + 40Y [Select] ✓Y [Select] X + 90Y [Select] ✓ Y ✓380 80 140arrow_forwardA farmer has 500 acres of available land and $100,000 to spend. He wants to plant the combination of crops which maximizes his profit. Complete parts (a) through (c). Profits and Constraints for Crops Potatoes Corn Number of Acres Cost (per acre) Profit (per acre) X₁ $320 $120 with Minimize subject to: y₁ +320y₂ 2 120. Y₁+1282 2 40 w = 500 y₁ + 100000 ₂ Y₁+224y > 60 Y₁ 20, y₂ 20 $128 $40 The farmer's estimated profit is $ (Simplity your answer.) Cabbage X3 $224 $60 S ≤ = Total 500 $100,000 Z (b) The solution to the dual problem can be interpreted as shadow profits. Use shadow profits to estimate the farmer's profit if land is cut to 400 acres but capital increases to $110,000.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice University
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Elementary Algebra
Algebra
ISBN:9780998625713
Author:Lynn Marecek, MaryAnne Anthony-Smith
Publisher:OpenStax - Rice University
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Solve ANY Optimization Problem in 5 Steps w/ Examples. What are they and How do you solve them?; Author: Ace Tutors;https://www.youtube.com/watch?v=BfOSKc_sncg;License: Standard YouTube License, CC-BY
Types of solution in LPP|Basic|Multiple solution|Unbounded|Infeasible|GTU|Special case of LP problem; Author: Mechanical Engineering Management;https://www.youtube.com/watch?v=F-D2WICq8Sk;License: Standard YouTube License, CC-BY
Optimization Problems in Calculus; Author: Professor Dave Explains;https://www.youtube.com/watch?v=q1U6AmIa_uQ;License: Standard YouTube License, CC-BY
Introduction to Optimization; Author: Math with Dr. Claire;https://www.youtube.com/watch?v=YLzgYm2tN8E;License: Standard YouTube License, CC-BY