
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Topic Video
Question
See attachment
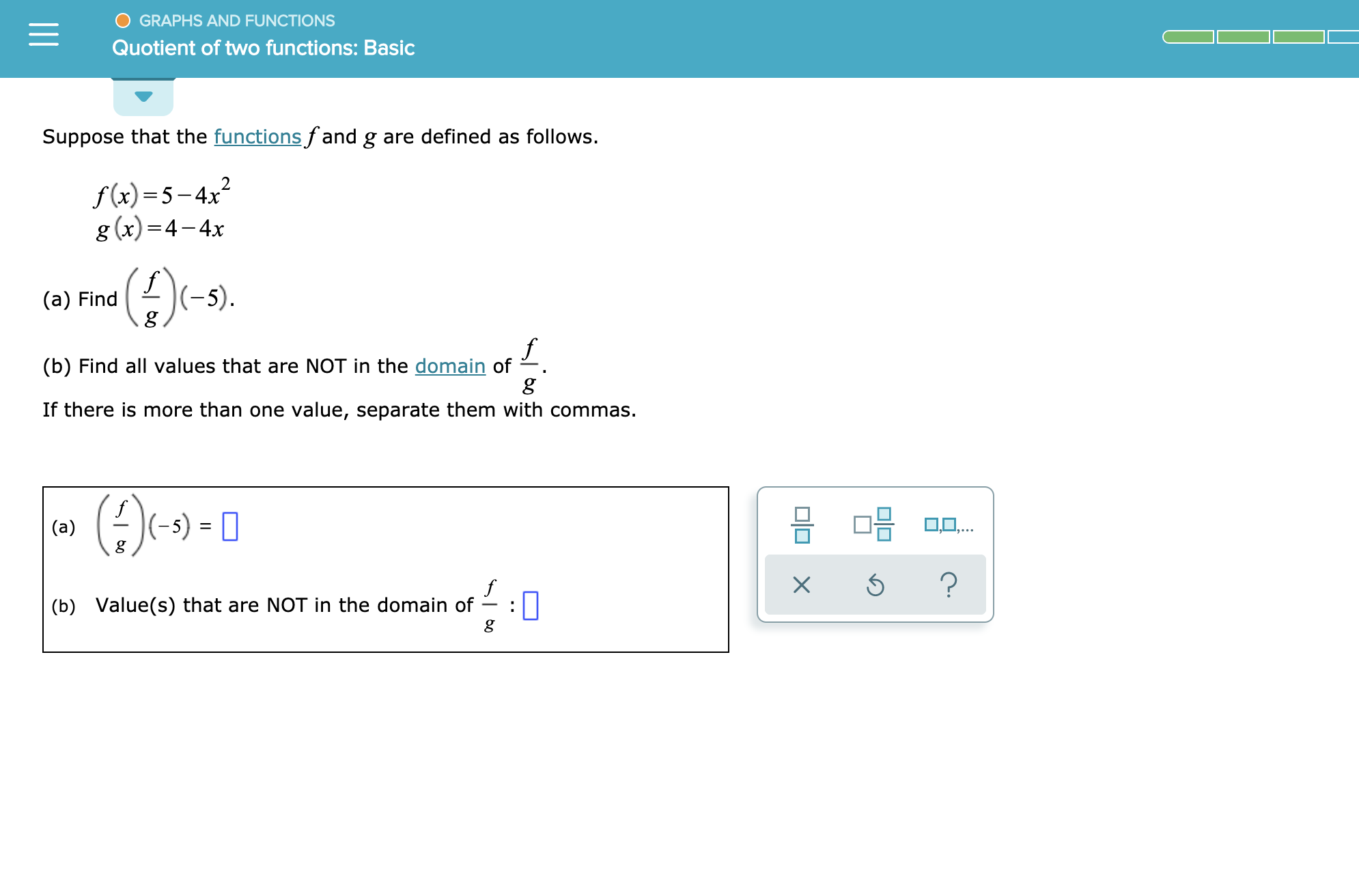
Transcribed Image Text:GRAPHS AND FUNCTIONS
Quotient of two functions: Basic
Suppose that the functions fand g are defined as follows.
f(x) 5-4x
g (x)4-4x
f
(-5).
(a) Find
f
(b) Find all values that are NOT in the domain of
g
If there is more than onee value, separate them with commas.
(Hn-O
(H)-
(-5) I
O,...
(a)
?
X
f
(b) Value(s) that are NOT in the domain of
g
:I
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
This is a popular solution
Trending nowThis is a popular solution!
Step by stepSolved in 4 steps with 4 images

Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Ornithologists have determined that some species of birds tend to avoid flights over large bodies of water during daylight hours. It is believed that more energy is required to fly over water than land because air generally rises over land and falls over water during the day. island 4 km 16 km W L D nest @ A bird with these tendencies is released from an island that is 4 km from the nearest point B on a straight shoreline, flies to a point C on the shoreline, and then flies along the shoreline to its nesting area D. Points B and D are 16 km apart. Assume that the bird instinctively chooses a path that will minimize its energy expenditure. (Round your answers to two decimal places.) (a) In general, if it takes 1.2 times as much energy to fly over water as land, to what point C should the bird fly in order to minimize the total energy expended in returning to its nesting area? km from B (b) Let W and L denote the energy (in joules) per kilometer flown over water and land, respectively.…arrow_forwardProve this statement "Regression models used for forecasting need not have a causal interpretation".?arrow_forwardEvaluate using integration by parts.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning
Calculus: Early TranscendentalsCalculusISBN:9781285741550Author:James StewartPublisher:Cengage Learning Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON
Thomas' Calculus (14th Edition)CalculusISBN:9780134438986Author:Joel R. Hass, Christopher E. Heil, Maurice D. WeirPublisher:PEARSON Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON
Calculus: Early Transcendentals (3rd Edition)CalculusISBN:9780134763644Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric SchulzPublisher:PEARSON Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
Calculus: Early TranscendentalsCalculusISBN:9781319050740Author:Jon Rogawski, Colin Adams, Robert FranzosaPublisher:W. H. Freeman
 Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning
Calculus: Early Transcendental FunctionsCalculusISBN:9781337552516Author:Ron Larson, Bruce H. EdwardsPublisher:Cengage Learning

Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning

Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON

Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON

Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman


Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning