
Advanced Engineering Mathematics
10th Edition
ISBN: 9780470458365
Author: Erwin Kreyszig
Publisher: Wiley, John & Sons, Incorporated
expand_more
expand_more
format_list_bulleted
Question
Transform the problem of finding mixed strategies into an equivalent linear programming problem.
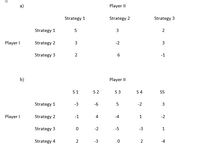
Transcribed Image Text:Player II
Strategy 1
Strategy 2
Strategy 3
Strategy 1
5
3
2
Player I
Strategy 2
3
-2
3
Strategy 3
2
6
-1
b)
Player II
S1
S2
S 3
S 4
S5
Strategy 1
-3
-6
-2
3
Player I
Strategy 2
-1
4.
-4
1
-2
Strategy 3
-2
-5
-3
Strategy 4
2
-3
-4
2.
5.
Expert Solution
This question has been solved!
Explore an expertly crafted, step-by-step solution for a thorough understanding of key concepts.
Step 1: Analysis and Introduction
VIEW Step 2: a) Check the payoff matrix follows mixed strategy or not.
VIEW Step 3: a) Form the LPP model for the provided two-person game
VIEW Step 4: b) Check the payoff matrix follows mixed strategy or not.
VIEW Step 5: b) Form the LPP model for the provided two-person game
VIEW Solution
VIEW Step by stepSolved in 6 steps with 55 images

Knowledge Booster
Similar questions
- Explain what Slack and Surplus variables in Linear programming and what are its functions in decision making process.arrow_forwardFormulate a linear programming problem that can be used to solve the following question. A firm has plants in Boston and Baltimore that manufacture three models of hot tubs: regular, fancy, and super. In one day the Boston plant can manufacture 32 of the regular model, 24 of the fancy model, and 12 of the super model, and costs $2500 per day to operate, whereas the Baltimore plant can manufacture 12 of the regular model, 16 of the fancy model, and 31 of the super model, and costs $2500 per day to operate. At least 312 of the regular model, 360 of the fancy model, and 456 of the super model are needed. How many days must each plant operate in order to minimize the cost? x = ---Select--- y = ---Select--- ---Select--- ✓| F= Subject to X --Select--- 0, y ---Select--- 0 (objective function) (regular models) (fancy models) (super models)arrow_forwarde3arrow_forward
- determine the equation of your model that will pass 2,4arrow_forwardAn investor has $621,000 to invest in bonds. Bond A yields an average of 8% and the bond B yields 7%. The investor requires that at least 5 times as much money be invested in bond A as in bond B. You must invest in these bonds to maximize his return. This can be set up as a linear programming problem. Introduce the decision variables: x= dollars invested in bond Ay= dollars invested in bond B Compute x+y. $ . Round to the nearest cent. Investor Matt has $152,000 to invest in bonds. Bond A yields an average of 9.2% and the bond B yields 8.4%. Matt requires that at least 4 times as much money be invested in bond A as in bond B. You must invest in these bonds to maximize his return. What is the maximum return? $ per year. Round to the nearest cent. Investor Dan has $607,000 to invest in bonds. Bond A yields an average of 8.5% and the bond B yields 8.4%. Dan requires that at least 4 times as much money be invested in bond A as in…arrow_forwardFormulate but do not solve the following exercise as a linear programming problem. Perth Mining Company operates two mines for the purpose of extracting gold and silver. The Saddle Mine costs $12,000/day to operate, and it yields 45 oz of gold and 3000 oz of silver each of x days. The Horseshoe Mine costs $14,000/day to operate, and it yields 80 oz of gold and 1250 oz of silver each of y days. Company management has set a target of at least 600 oz of gold and 16,000 oz of silver. How many days should each mine be operated so that the target can be met at a minimum cost C in dollars? Minimize C = subject to the constraints gold silverarrow_forward
- Formulate but do not solve the following exercise as a linear programming problem.National Business Machines manufactures x model A fax machines and y model B fax machines. Each model A cost $120 to make, and each model B costs $150. The profits are $30 for each model A and $30 for each model B fax machine. If the total number of fax machines demanded per month does not exceed 1900 and the company has earmarked not more than $600,000/month for manufacturing costs, how many units of each model should National make each month to maximize its monthly profits P in dollars ? Maximize P = subject to the constraints manufacturing costs number produced x ≥ 0 y ≥ 0arrow_forwardSolve the following linear programming problem. You are taking two dietary supplements daily: Supplement A and Supplement B. An ounce of supplement A contains 9 units of calcium, 8 units of vitamin D, and 5 units of sodium. An ounce of supplement B contains 2 units of calcium, 4 units of vitamin D, and 3 units of sodium. Your goal is to get at least 90 units of calcium and at least 120 units of vitamin D from the supplements daily, while at the same time reducing the amount of sodium that you will get. How many ounces of each supplement should you take daily to reach your goals? Ounces of Supplement A = Blank 1. Fill in the blank, read surrounding text. Ounces of Supplement B = Blank 2. Fill in the blank, read surrounding text. How many units of sodium will you get daily under these circumstances? Units of Sodium = Blank 3. Fill in the blank, read surrounding text.arrow_forwardFormulate but do not solve the following exercise as a linear programming problem. A financier plans to invest up to $400,000 in two projects. Project A yields a return of 10% on the investment of x dollars, whereas Project B yields a return of 13% on the investment of y dollars. Because the investment in Project B is riskier than the investment in Project A, the financier has decided that the investment in Project B should not exceed 40% of the total investment. How much should she invest in each project to maximize the return on her investment P in dollars? MaximizeP= subject to the constraints ? amount available for investment? allocation of funds?arrow_forward
- Use Excel to solve the linear programming problem.At one of its factories, a manufacturer of televisions makes one or more of four models of HD units (without cases): a 20-in. LCD, a 42-in. LCD, a 42-in. plasma, and a 50-in. plasma. The assembly and testing time requirements for each model are shown in the table, together with the maximum amounts of time available per week for assembly and testing. In addition to these constraints, the supplier of cases indicated that it would supply no more than 290 cases per week and that of these, no more than 40 could be for the 20-in. LCD model.Use the profit for each television shown in the table to find the number of completed models of each type that should be produced to obtain the maximum profit for the week. Find the maximum profit. 20-in. LCD sets 42-in. LCD sets 42-in. plasma sets 50-in. plasma sets profit $ 20-in.LCD 42-in.LCD 42-in.Plasma 50-in.Plasma TotalAvailable Assembly time…arrow_forwardFormulate but do not solve the following exercise as a linear programming problem.A company manufactures x units of Product A and y units of Product B, on two machines, I and II. It has been determined that the company will realize a profit of $3 on each unit of Product A and $5 on each unit of Product B. To manufacture a unit of Product A requires 5 min on Machine I and 5 min on Machine II. To manufacture a unit of Product B requires 9 min on Machine I and 5 min on Machine II. There are 269 min available on Machine I and 205 min available on Machine II in each work shift. How many units of a product should be produced in each shift to maximize the company's profit P in dollars? Maximize P = subject to the constraints Machine I Machine II x ≥ 0 y ≥ 0arrow_forwardFormulate but do not solve the following exercise as a linear programming problem. A nutritionist at the Medical Center has been asked to prepare a special diet for certain patients. She has decided that the meals are to be prepared from Foods A and B and that the meals should contain a minimum of 390 mg of calcium, 10 mg of iron, and 40 mg of vitamin C. Each ounce of Food A contains 25 mg of calcium, 2.5 mg of iron, 2 mg of vitamin C, and 6 mg of cholesterol. Each ounce of Food B contains 25 mg of calcium, 0.5 mg of iron, 5 mg of vitamin C, and 5 mg of cholesterol. How many ounces of each type of food should be used in a meal so that the cholesterol content C (in mg) is minimized and the minimum requirements of calcium, iron, and vitamin C are met? Minimize C = subject to the constraints calcium iron vitamin C x ≥ 0 y ≥ 0arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,


Advanced Engineering Mathematics
Advanced Math
ISBN:9780470458365
Author:Erwin Kreyszig
Publisher:Wiley, John & Sons, Incorporated

Numerical Methods for Engineers
Advanced Math
ISBN:9780073397924
Author:Steven C. Chapra Dr., Raymond P. Canale
Publisher:McGraw-Hill Education

Introductory Mathematics for Engineering Applicat...
Advanced Math
ISBN:9781118141809
Author:Nathan Klingbeil
Publisher:WILEY

Mathematics For Machine Technology
Advanced Math
ISBN:9781337798310
Author:Peterson, John.
Publisher:Cengage Learning,

