Math
Discrete Mathematics With ApplicationsFor each pair of graphs G and G’ in 6-13, determine whether G and G’ are isomorphic. If they are, give functions g: V(G) → V(G’) and h:E(G) → E(G’) that define the isomorphism. If they are not, give an invariant for graph isomorphism that they do not share.
close solutoin list

For each pair of graphs G and G’ in 6-13, determine whether G and G’ are isomorphic. If they are, give functions g: V(G) → V(G’) and h:E(G) → E(G’) that define the isomorphism. If they are not, give an invariant for graph isomorphism that they do not share.

BuyFind

Discrete Mathematics With Applicat...

5th Edition
EPP + 1 other
Publisher: Cengage Learning,
ISBN: 9781337694193
BuyFind

Discrete Mathematics With Applicat...

5th Edition
EPP + 1 other
Publisher: Cengage Learning,
ISBN: 9781337694193

Solutions

Chapter
Section
Problem 1TY
Problem 2TY
Problem 3TY
Problem 1ES
Problem 2ES
Problem 3ES
Problem 4ES
Problem 5ES
Problem 6ES
Problem 7ES
Problem 8ES
Problem 9ES
Problem 10ES
Problem 11ES
Problem 12ES
Problem 13ES
Problem 14ES
Problem 15ES
Problem 16ES
Problem 17ES
Problem 18ES
Problem 19ES
Problem 20ES
Problem 21ES
Problem 22ES
Problem 23ES
Problem 24ES
Problem 25ES
Problem 26ES
Problem 27ES
Problem 28ES
Problem 29ES
Problem 30ES
Chapter 10.3, Problem 13ES
Textbook Problem

For each pair of graphs G and G’ in 6-13, determine whether G and G’ are isomorphic. If they are, give functions g: V(G) → V(G’) and h:E(G) → E(G’) that define the isomorphism. If they are not, give an invariant for graph isomorphism that they do not share.

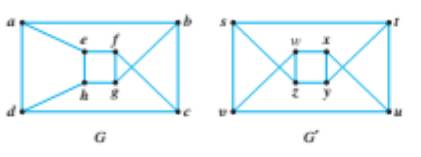
Chapter 10.3, Problem 13ES, For each pair of graphs G and G’ in 6-13, determine whether G and G’ are isomorphic. If they are,

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.See solution
Chapter 10.3,
Problem 12ES
Chapter 10.3,
Problem 14ES

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

See Solution

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 10 Solutions

Discrete Mathematics With Applications
Show all chapter solutions
Ch. 10.1 - Let G be a graph and let v and w be vertices in G....Ch. 10.1 - A graph is connected if, any only if, _____.Ch. 10.1 - Removing an edge from a circuit in a graph does...Ch. 10.1 - An Euler circuit in graph is _____.Ch. 10.1 - A graph has a Euler circuit if, and only if,...Ch. 10.1 - Given vertices v and w in a graph, there is an...Ch. 10.1 - A Hamiltonian circuit in a graph is ______.Ch. 10.1 - If a graph G has a Hamiltonian circuit, then G has...Ch. 10.1 - A travelling salesman problem involves finding a...Ch. 10.1 - In the graph below, determine whether the...
Ch. 10.1 - In the graph below, determine whether the...Ch. 10.1 - Let G be the graph and consider the walk...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - An edge whose removal disconnects the graph of...Ch. 10.1 - Given any positive integer n, (a) find a connected...Ch. 10.1 - Find the number of connected components for each...Ch. 10.1 - Each of (a)—(c) describes a graph. In each case...Ch. 10.1 - The solution for Example 10.1.6 shows a graph for...Ch. 10.1 - Is it possible for a citizen of Königsberg to make...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Is it possible to take a walk around the city...Ch. 10.1 - For each of the graph in 19-21, determine whether...Ch. 10.1 - For each of the graph in 19-21, determine whether...Ch. 10.1 - For each of the graph in 19-21, determine whether...Ch. 10.1 - The following is a floor plan of a house. Is it...Ch. 10.1 - Find all subgraph of each of the following graphs.Ch. 10.1 - Find the complement of each of the following...Ch. 10.1 - Find the complement of the graph K4, the complete...Ch. 10.1 - Suppose that in a group of five people A,B,C,D,...Ch. 10.1 - Let G be a simple graph with n vertices. What is...Ch. 10.1 - Show that at a party with at least two people,...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Show that none of graphs in 31-33 has a...Ch. 10.1 - Show that none of graphs in 31-33 has a...Ch. 10.1 - Show that none of graphs in 31-33 has a...Ch. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - Give two examples of graphs that have Hamiltonian...Ch. 10.1 - Give two examples of graphs that have circuits...Ch. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - A traveler in Europe wants to visit each of the...Ch. 10.1 - a. Prove that if a walk in a graph contains a...Ch. 10.1 - Prove Lemma 10.1.1(a): If G is a connected graph,...Ch. 10.1 - Prove Lemma 10.1.1(b): If vertices v and w are...Ch. 10.1 - Draw a picture to illustrate Lemma 10.1.1(c): If a...Ch. 10.1 - Prove that if there is a trail in a graph G from a...Ch. 10.1 - If a graph contains a circuits that starts and...Ch. 10.1 - Prove that if there is a circuit in a graph that...Ch. 10.1 - Let G be a connected graph, and let C be any...Ch. 10.1 - Prove that any graph with an Euler circuit is...Ch. 10.1 - Prove Corollary 10.1.5.Ch. 10.1 - For what values of n dies the complete graph Kn...Ch. 10.1 - For what values of m and n does the complete...Ch. 10.1 - What is the maximum number of edges a simple...Ch. 10.1 - Prove that if G is any bipartite graph, then every...Ch. 10.1 - An alternative proof for Theorem 10.1.3 has the...Ch. 10.2 - In the adjacency matrix for a directed graph, the...Ch. 10.2 - In the adjacency matrix for an undirected graph,...Ch. 10.2 - An n × n square matrix is called symmetric if, and...Ch. 10.2 - The ijth entry in the produce of two matrices A...Ch. 10.2 - In an n × n identity matrix, the entries on the...Ch. 10.2 - If G is a graph with vertices v1, v2, …., vn and A...Ch. 10.2 - Find real numbers a, b, and c such that the...Ch. 10.2 - Find the adjacency matrices for the following...Ch. 10.2 - Find directed graphs that have the following...Ch. 10.2 - Find adjacency matrices for the following...Ch. 10.2 - Find graphs that have the following adjacency...Ch. 10.2 - The following are adjacency matrices for graphs....Ch. 10.2 - Suppose that for every positive integer I, all the...Ch. 10.2 - Find each of the following products. [21][13]...Ch. 10.2 - Find each of the following products? a....Ch. 10.2 - Let A = [ 1 1 1 0 2 1] , B = [ 2 0 1 3] and C =...Ch. 10.2 - Give an example different from that in the text to...Ch. 10.2 - Let O denote the matrix [0000] . Find 2 × 2...Ch. 10.2 - Let O denote the matrix [0000] . Find 2 × 2...Ch. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - In 14—18, assume the entries of all matrices are...Ch. 10.2 - Let A = [112101210] . Find A2 and A3. Let G be the...Ch. 10.2 - The following is an adjacency matrix for a graph:...Ch. 10.2 - Let A be the adjacency matrix for K3, the complete...Ch. 10.2 - Draw a graph that has [0001200011000211120021100]...Ch. 10.2 - Let G be a graph with n vertices, and let v and w...Ch. 10.3 - If G and G’ are graphs, then G is isomorphic to G’...Ch. 10.3 - A property P is an invariant for graph isomorphism...Ch. 10.3 - Some invariants for graph isomorphism are , , , ,...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G in 1—5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of simple graphs G and G in 6—13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Draw all nonisomorphic simple graphs with three...Ch. 10.3 - Draw all nonisomorphic simple graphs with four...Ch. 10.3 - Draw all nonisomorphic graphs with three vertices...Ch. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Draw all nonisomorphic graphs with six vertices,...Ch. 10.3 - Draw four nonisomorphic graphs with six vertices,...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Show that the following two graphs are not...Ch. 10.4 - A circuit-free graph is a graph with __________.Ch. 10.4 - A forest is a graph that is _________, and a tree...Ch. 10.4 - A trivial tree is a graph that consists of...Ch. 10.4 - Any tree with at least two vertices has at least...Ch. 10.4 - If a tree T has at least two vertices, then a...Ch. 10.4 - For any positive integer n, any tree with n...Ch. 10.4 - For any positive integer n, if G is a connected...Ch. 10.4 - Read the tree in Example 10.4.2 from left to right...Ch. 10.4 - Draw trees to show the derivations of the...Ch. 10.4 - What is the total degree of a tree with n...Ch. 10.4 - Let G be the graph of a hydrocarbon molecule with...Ch. 10.4 - Extend the argument given in the proof of Lemma...Ch. 10.4 - If graphs are allowed to have an infinite number...Ch. 10.4 - Find all leaves (or terminal vertices) and all...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - A connected graph has twelve vertices and eleven...Ch. 10.4 - A connected graph has nine vertices and twelve...Ch. 10.4 - Suppose that v is a vertex of degree 1 in a...Ch. 10.4 - A graph has eight vertices and six edges. Is it...Ch. 10.4 - If a graph has n vertices and n2 or fewer can it...Ch. 10.4 - A circuit-free graph has ten vertices and nine...Ch. 10.4 - Is a circuit-free graph with n vertices and at...Ch. 10.4 - Prove that every nontrivial tree has at least two...Ch. 10.4 - Find all nonisomorphic trees with five vertices.Ch. 10.4 - a. Prove that the following is an invariant for...Ch. 10.5 - A rooted tree is a tree in which . The level of a...Ch. 10.5 - A binary tree is a rooted tree in which .Ch. 10.5 - A full binary tree is a rooted tree in which .Ch. 10.5 - If k is a positive integer and T is a full binary...Ch. 10.5 - If T is a binary tree that has t leaves and height...Ch. 10.5 - Consider the tree shown below with root a. a. What...Ch. 10.5 - Consider the tree shown below with root v0 . a....Ch. 10.5 - Draw binary trees to represent the following...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In each of 4—20, either draw a graph with the...Ch. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.6 - A spanning tree for a graph G is .Ch. 10.6 - A weighted graph is a graph for which and the...Ch. 10.6 - A minimum spanning tree for a connected, weighted...Ch. 10.6 - In Kruskal’s algorithm, the edges of a connected,...Ch. 10.6 - In Prim’s algorithm, a minimum spanning tree is...Ch. 10.6 - In Dijkstra’s algorithm, a vertex is in the fringe...Ch. 10.6 - At each stage of Dijkstra’s algorithm, the vertex...Ch. 10.6 - Find all possible spanning trees for each of the...Ch. 10.6 - Find all possible spanning trees for each of the...Ch. 10.6 - Find a spanning trees for each of the graphs in 3...Ch. 10.6 - Find a spanning trees for each of the graphs in 3...Ch. 10.6 - Use Kruskal’s algorithm to find a minimum spanning...Ch. 10.6 - Use Kruskal’s algorithm to find a minimum spanning...Ch. 10.6 - Use Prim’s algorithm starting with vertex a or...Ch. 10.6 - Use Prim’s algorithm starting with vertex a or...Ch. 10.6 - For each of the graphs in 9 and 10, find all...Ch. 10.6 - For each of the graphs in 9 and 10, find all...Ch. 10.6 - A pipeline is to be built that will link six...Ch. 10.6 - Use Dijkstra’s algorithm for the airline route...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Prove part (2) of Proposition 10.6.1: Any two...Ch. 10.6 - Given any two distinct vertices of a tree, there...Ch. 10.6 - Prove that if G is a graph with spanning tree T...Ch. 10.6 - Suppose G is a connected graph and T is a...Ch. 10.6 - a. Suppose T1 and T2 are two different spanning...Ch. 10.6 - Prove that an edge e is contained in every...Ch. 10.6 - Consider the spanning trees T1and T2in the proof...Ch. 10.6 - Suppose that T is a minimum spanning tree for a...Ch. 10.6 - Prove that if G is a connected, weighted graph and...Ch. 10.6 - If G is a connected, weighted graph and no two...Ch. 10.6 - Prove that if G is a connected, weighted graph and...Ch. 10.6 - Suppose a disconnected graph is input to Kruskal’s...Ch. 10.6 - Suppose a disconnected graph is input to Prim’s...Ch. 10.6 - Modify Algorithm 10.6.3 so that the output...Ch. 10.6 - Prove that if a connected, weighted graph G is...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Show solutions
Sketch the graphs of the equations in Exercises 512. x2y=1

Finite Mathematics

Find the range, the standard deviation, and the variance for the given samples. Round noninteger results to the...

Mathematical Excursions (MindTap Course List)

For each pair of supply-and-demand equations in Exercises 22-25, where x represents the quantity demanded in un...

Finite Mathematics for the Managerial, Life, and Social Sciences

The Census Bureau in Census 2010 reported the 2010 national and regional populations in Figure 11.42. The Censu...

Mathematics: A Practical Odyssey

In Problems 20-25, use the sum formulas I-V to express each of the following without the summation symbol. In P...

Mathematical Applications for the Management, Life, and Social Sciences

Solve each of the following problems using the proper order of operations. 19(3)(2)+(5)2

Mathematics For Machine Technology

For each general triangle, a. determine the number of solutions and) b. solve the triangle, if possible, using ...

Elementary Technical Mathematics

Examining a Partial Derivative In Exercises 5-10, explain whether the Quotient Rule should he used to find the ...

Calculus

Sketch the region enclosed by the given curves and find its area. x = y4, y=2x, y = 0

Single Variable Calculus: Early Transcendentals, Volume I

Suppose that three points on the parabola y = x2 have the property that their nom1al lines intersect at a commo...

Calculus: Early Transcendentals

In Exercises 9 to 24, find an equation of the line described. Leave the solution in the form Ax+By = C. The lin...

Elementary Geometry for College Students

Finding an Indefinite Integral In Exercises 526, find the indefinite integral and check the result by different...

Calculus: Early Transcendental Functions (MindTap Course List)

Sharing a Job Jack, Kay, and Lynn deliver advertising flyers in a small town. If each person works alone, it ta...

Precalculus: Mathematics for Calculus (Standalone Book)

Complete each statement: a If a quadrilateral has two pair of congruent adjacent sides, then the quadrilateral ...

Elementary Geometry For College Students, 7e

In Exercises 5762, sketch the straight line defined by the given linear equation by finding the x- and y-interc...

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

Reminder Round all answers to two decimal places unless otherwise indicated. Falling Rocks The following table ...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

If a0 and ab, then prove or disprove that (a,b)=a.

Elements Of Modern Algebra

Jamie and Alice Newmark have a combined monthly gross income of $9,702 and monthly expenses totaling $2,811. Th...

Contemporary Mathematics for Business & Consumers

With an initial estimate of −1, use Newton’s Method once to estimate a zero of f(x) = 5x2 + 15x + 9.

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

The article Microwave Observations of Daily Antarctic Sea-Ice Edge Expansion and Contribution Rates (IEEE Geosc...

Probability and Statistics for Engineering and the Sciences

Colleges’ Cost and Percent Graduated. Refer to the data set in Table 2.18. Prepare a scatter diagram to show th...

Essentials Of Statistics For Business & Economics

Exercises You can use the following problems as a self-test on the material presented in this review. If you ca...

Essentials Of Statistics

The Grocery Manufacturers of America reported that 76% of consumers read the ingredients listed on a products l...

Statistics for Business & Economics, Revised (MindTap Course List)

Use the guidelines of Section 3.5 to sketch the curve. 26. y = x2/3(x 3)2

Single Variable Calculus

Determine whether the given expression is a polynomial. If so, tell whether it is a monomial, a binomial, or a ...

College Algebra (MindTap Course List)

By the method of undetermined coefficients, a particular solution to y″ − 5y′ + 6y = e4x will have the form: yp...

Study Guide for Stewart's Multivariable Calculus, 8th

Solve the differential equation. 6. d2ydx2+dydx2y=x2

Multivariable Calculus

Find the first partial derivatives of the function. F(x,y)=yxcos(et)dt

Calculus (MindTap Course List)

Calculate each expression in Exercises 124, giving the answer as a whole number or a fraction in lowest terms. ...

Finite Mathematics and Applied Calculus (MindTap Course List)

The Economic Policy Institute periodically issues reports on wages of entry level workers. The institute report...

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Business Ethics: Privacy According to the same poll quoted in Problem 24, 53% of adults are concerned that Soci...

Understanding Basic Statistics

Slant Asymptote In Exercises 7176, use a graphing utility to graph the function and determine the slant asympto...

Calculus (MindTap Course List)

Prove the statement using the , definition of a limit. limx4x22x8x4=6

Single Variable Calculus: Early Transcendentals

Using Formulas In Exercises 77-412, find the indefinite integral by using the appropriate formula from Exercise...

Calculus of a Single Variable

Describe how experimenter bias can be a threat to internal validity; that is, how can experimenter bias provide...

Research Methods for the Behavioral Sciences (MindTap Course List)

One sample of n = 10 scores has a mean of 8 and a second sample of n 5 scores has a mean of 2. If the two samp...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

Find all possible real solutions of each equation in Exercises 3144. x3x23x+3=0

Applied Calculus

In Exercises 13 and 14, determine whether y is a function of x. 9x2+4y2=49

Calculus: An Applied Approach (MindTap Course List)

HOW DO YOU SEE IT? The four figures below are graphs of the vector-valued function r(t)=4costi+4sintj+t4k Match...

Multivariable Calculus

For Problems 11-18, from the list 0,14,23,,7,1114,2.34,19,558,17,3.21,and2.6, identify each of the following. O...

Intermediate Algebra

The following two relative frequency distributions are based on data that appeared in The Chronicle of Higher E...

Introduction To Statistics And Data Analysis

Briefly explain what is meant when a researcher reports a significant mean difference between two treatment con...

Research Methods for the Behavioral Sciences (MindTap Course List)

A random sample is selected from a normal population with a mean of =30and a standard deviation of =8 . After a...

Statistics for The Behavioral Sciences (MindTap Course List)

Proof Prove that the principal unit normal vector N points toward the concave side of a plane curve.

Calculus: Early Transcendental Functions

Draw each of the following angles in standard position, find a point on the terminal side, and then find the si...

Trigonometry (MindTap Course List)

In the following exercises, solve for the antiderivative f of f with C = 0, then use a calculator to graph f an...

Calculus Volume 2

In Problems 1720 the indicated function y1(x) is a solution of the associated homogeneous equation. Use the met...

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

In the following exercises, use the following graph of function y=f(x) to find the values, if possible. Estimat...

Calculus Volume 1

A gross of eggs contains 144 eggs. A particular gross Is known to have 12 cracked eggs. An Inspector randomly c...

Introductory Statistics

Finding the Slope of a Line Through Two Points In Exercises 25-34, find the slope of the line passing through t...

College Algebra

30. To estimate the mean age for a population of 4000 employees, a simple random sample of 40 employees is sele...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.