
Discrete Mathematics With Applications
5th Edition
ISBN: 9781337694193
Author: EPP, Susanna S.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10.3, Problem 7ES
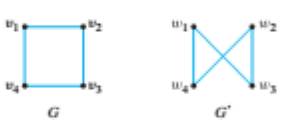
For each pair of graphs G and G’ in 6-13, determine whether G and G’ are isomorphic. If they are, give functions g: V(G)
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
Let G be an undirected graph with a loop at every vertex.Show that the relation R on the set of vertices of G suchthat uRv if and only if there is an edge associated to {u, v}is a symmetric, reflexive relation on G.
Prove that graphs G1 and G2 are isomorphic.
Suppose that G is an r-regular graph of order n such that both G and its complement G are connected. Is it possible that neither G nor G is Eulerian?
Chapter 10 Solutions
Discrete Mathematics With Applications
Ch. 10.1 - Let G be a graph and let v and w be vertices in G....Ch. 10.1 - A graph is connected if, any only if, _____.Ch. 10.1 - Removing an edge from a circuit in a graph does...Ch. 10.1 - An Euler circuit in graph is _____.Ch. 10.1 - Prob. 5TYCh. 10.1 - Prob. 6TYCh. 10.1 - Prob. 7TYCh. 10.1 - If a graph G has a Hamiltonian circuit, then G has...Ch. 10.1 - A travelling salesman problem involves finding a...Ch. 10.1 - In the graph below, determine whether the...
Ch. 10.1 - In the graph below, determine whether the...Ch. 10.1 - Let G be the graph and consider the walk...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - An edge whose removal disconnects the graph of...Ch. 10.1 - Given any positive integer n, (a) find a connected...Ch. 10.1 - Find the number of connected components for each...Ch. 10.1 - Each of (a)—(c) describes a graph. In each case...Ch. 10.1 - Prob. 10ESCh. 10.1 - Is it possible for a citizen of Königsberg to make...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Is it possible to take a walk around the city...Ch. 10.1 - For each of the graph in 19-21, determine whether...Ch. 10.1 - Prob. 20ESCh. 10.1 - Prob. 21ESCh. 10.1 - Prob. 22ESCh. 10.1 - Prob. 23ESCh. 10.1 - Find the complement of each of the following...Ch. 10.1 - Find the complement of the graph K4, the complete...Ch. 10.1 - Suppose that in a group of five people A,B,C,D,...Ch. 10.1 - Prob. 27ESCh. 10.1 - Show that at a party with at least two people,...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Prob. 31ESCh. 10.1 - Show that none of graphs in 31-33 has a...Ch. 10.1 - Prob. 33ESCh. 10.1 - Prob. 34ESCh. 10.1 - Prob. 35ESCh. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - Prob. 37ESCh. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - Prob. 39ESCh. 10.1 - Prob. 40ESCh. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - A traveler in Europe wants to visit each of the...Ch. 10.1 - a. Prove that if a walk in a graph contains a...Ch. 10.1 - Prob. 44ESCh. 10.1 - Prob. 45ESCh. 10.1 - Prob. 46ESCh. 10.1 - Prove that if there is a trail in a graph G from a...Ch. 10.1 - If a graph contains a circuits that starts and...Ch. 10.1 - Prob. 49ESCh. 10.1 - Let G be a connected graph, and let C be any...Ch. 10.1 - Prob. 51ESCh. 10.1 - Prob. 52ESCh. 10.1 - For what values of n dies the complete graph Kn...Ch. 10.1 - For what values of m and n does the complete...Ch. 10.1 - What is the maximum number of edges a simple...Ch. 10.1 - Prob. 56ESCh. 10.1 - Prob. 57ESCh. 10.2 - In the adjacency matrix for a directed graph, the...Ch. 10.2 - Prob. 2TYCh. 10.2 - Prob. 3TYCh. 10.2 - Prob. 4TYCh. 10.2 - Prob. 5TYCh. 10.2 - Prob. 6TYCh. 10.2 - Find real numbers a, b, and c such that the...Ch. 10.2 - Find the adjacency matrices for the following...Ch. 10.2 - Find directed graphs that have the following...Ch. 10.2 - Find adjacency matrices for the following...Ch. 10.2 - Find graphs that have the following adjacency...Ch. 10.2 - Prob. 6ESCh. 10.2 - Prob. 7ESCh. 10.2 - Prob. 8ESCh. 10.2 - Prob. 9ESCh. 10.2 - Prob. 10ESCh. 10.2 - Prob. 11ESCh. 10.2 - Prob. 12ESCh. 10.2 - Let O denote the matrix [0000] . Find 2 × 2...Ch. 10.2 - Prob. 14ESCh. 10.2 - Prob. 15ESCh. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - Prob. 17ESCh. 10.2 - Prob. 18ESCh. 10.2 - Prob. 19ESCh. 10.2 - The following is an adjacency matrix for a graph:...Ch. 10.2 - Let A be the adjacency matrix for K3, the complete...Ch. 10.2 - Draw a graph that has [0001200011000211120021100]...Ch. 10.2 - Prob. 23ESCh. 10.3 - If G and G’ are graphs, then G is isomorphic to G’...Ch. 10.3 - A property P is an invariant for graph isomorphism...Ch. 10.3 - Prob. 3TYCh. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G in 1—5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Prob. 9ESCh. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of simple graphs G and G in 6—13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Draw all nonisomorphic simple graphs with three...Ch. 10.3 - Draw all nonisomorphic simple graphs with four...Ch. 10.3 - Prob. 16ESCh. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Prob. 19ESCh. 10.3 - Draw four nonisomorphic graphs with six vertices,...Ch. 10.3 - Prob. 21ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 23ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 25ESCh. 10.3 - Prob. 26ESCh. 10.3 - Prob. 27ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 29ESCh. 10.3 - Show that the following two graphs are not...Ch. 10.4 - A circuit-free graph is a graph with __________.Ch. 10.4 - Prob. 2TYCh. 10.4 - Prob. 3TYCh. 10.4 - Prob. 4TYCh. 10.4 - Prob. 5TYCh. 10.4 - Prob. 6TYCh. 10.4 - For any positive integer n, if G is a connected...Ch. 10.4 - Read the tree in Example 10.4.2 from left to right...Ch. 10.4 - Prob. 2ESCh. 10.4 - Prob. 3ESCh. 10.4 - Prob. 4ESCh. 10.4 - Prob. 5ESCh. 10.4 - Prob. 6ESCh. 10.4 - Prob. 7ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - Prob. 14ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - Prob. 17ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - A connected graph has twelve vertices and eleven...Ch. 10.4 - A connected graph has nine vertices and twelve...Ch. 10.4 - Prob. 24ESCh. 10.4 - Prob. 25ESCh. 10.4 - If a graph has n vertices and n2 or fewer can it...Ch. 10.4 - A circuit-free graph has ten vertices and nine...Ch. 10.4 - Is a circuit-free graph with n vertices and at...Ch. 10.4 - Prob. 29ESCh. 10.4 - Prob. 30ESCh. 10.4 - a. Prove that the following is an invariant for...Ch. 10.5 - Prob. 1TYCh. 10.5 - Prob. 2TYCh. 10.5 - Prob. 3TYCh. 10.5 - Prob. 4TYCh. 10.5 - Prob. 5TYCh. 10.5 - Prob. 1ESCh. 10.5 - Prob. 2ESCh. 10.5 - Draw binary trees to represent the following...Ch. 10.5 - Prob. 4ESCh. 10.5 - Prob. 5ESCh. 10.5 - Prob. 6ESCh. 10.5 - Prob. 7ESCh. 10.5 - Prob. 8ESCh. 10.5 - Prob. 9ESCh. 10.5 - Prob. 10ESCh. 10.5 - Prob. 11ESCh. 10.5 - Prob. 12ESCh. 10.5 - Prob. 13ESCh. 10.5 - Prob. 14ESCh. 10.5 - Prob. 15ESCh. 10.5 - Prob. 16ESCh. 10.5 - Prob. 17ESCh. 10.5 - Prob. 18ESCh. 10.5 - Prob. 19ESCh. 10.5 - Prob. 20ESCh. 10.5 - Prob. 21ESCh. 10.5 - Prob. 22ESCh. 10.5 - Prob. 23ESCh. 10.5 - Prob. 24ESCh. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.6 - Prob. 1TYCh. 10.6 - Prob. 2TYCh. 10.6 - Prob. 3TYCh. 10.6 - In Kruskal’s algorithm, the edges of a connected,...Ch. 10.6 - Prob. 5TYCh. 10.6 - Prob. 6TYCh. 10.6 - At each stage of Dijkstra’s algorithm, the vertex...Ch. 10.6 - Prob. 1ESCh. 10.6 - Prob. 2ESCh. 10.6 - Prob. 3ESCh. 10.6 - Prob. 4ESCh. 10.6 - Prob. 5ESCh. 10.6 - Prob. 6ESCh. 10.6 - Prob. 7ESCh. 10.6 - Prob. 8ESCh. 10.6 - Prob. 9ESCh. 10.6 - Prob. 10ESCh. 10.6 - A pipeline is to be built that will link six...Ch. 10.6 - Use Dijkstra’s algorithm for the airline route...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Prob. 17ESCh. 10.6 - Prob. 18ESCh. 10.6 - Prob. 19ESCh. 10.6 - Prob. 20ESCh. 10.6 - Prob. 21ESCh. 10.6 - Prob. 22ESCh. 10.6 - Prob. 23ESCh. 10.6 - Prob. 24ESCh. 10.6 - Prob. 25ESCh. 10.6 - Prob. 26ESCh. 10.6 - Prob. 27ESCh. 10.6 - Suppose a disconnected graph is input to Kruskal’s...Ch. 10.6 - Suppose a disconnected graph is input to Prim’s...Ch. 10.6 - Modify Algorithm 10.6.3 so that the output...Ch. 10.6 - Prob. 31ES
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 17. Find two groups and such that is a homomorphic image of but is not a homomorphic image of . (Thus the relation in Exercise does not have the symmetric property.) Exercise 15: 15. Prove that on a given collection of groups, the relation of being a homomorphic image has the reflexive property.arrow_forward16. Suppose that and are groups. If is a homomorphic image of , and is a homomorphic image of , prove that is a homomorphic image of . (Thus the relation in Exercise has the transitive property.) Exercise 15: 15. Prove that on a given collection of groups, the relation of being a homomorphic image has the reflexive property.arrow_forwardLabel each of the following statements as either true or false. The relation of being a homomorphic image is an equivalence relation on a collection of groups.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,
Elements Of Modern AlgebraAlgebraISBN:9781285463230Author:Gilbert, Linda, JimmiePublisher:Cengage Learning,

Elements Of Modern Algebra
Algebra
ISBN:9781285463230
Author:Gilbert, Linda, Jimmie
Publisher:Cengage Learning,
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY