
Discrete Mathematics With Applications
5th Edition
ISBN: 9781337694193
Author: EPP, Susanna S.
Publisher: Cengage Learning,
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10.1, Problem 42ES
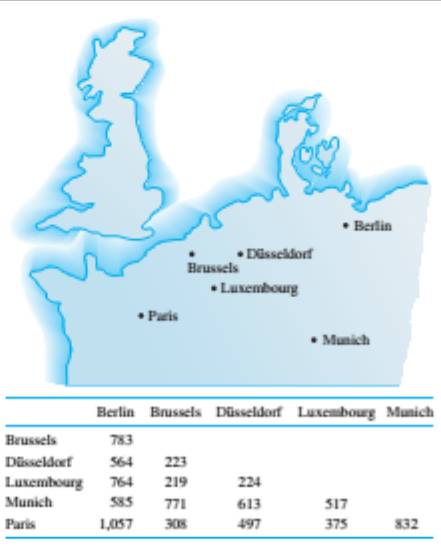
A traveler in Europe wants to visit each of the cities shown on the map exactly once, starting and ending in Brussels. The distance (in kilometer) between each pair of cities is given in the table. Find a Hamiltonian circuit that minimizes the total distance traveled. (Use the map to narrow the possible circuit down to just a few. Then use the table to find the total distance for each of those.)
Expert Solution & Answer
Trending nowThis is a popular solution!

Students have asked these similar questions
Starting with the given flow (in brackets), apply the Ford-Fulkerson procedure to the network below to find the maximum flow.
Solve the following network question by using Maximal Flow Method. Calculate the maximal flow from 1st node to 6thnode
Determine the value of x, y, and z using Gauss-Jordan Reduction Method
Chapter 10 Solutions
Discrete Mathematics With Applications
Ch. 10.1 - Let G be a graph and let v and w be vertices in G....Ch. 10.1 - A graph is connected if, any only if, _____.Ch. 10.1 - Removing an edge from a circuit in a graph does...Ch. 10.1 - An Euler circuit in graph is _____.Ch. 10.1 - Prob. 5TYCh. 10.1 - Prob. 6TYCh. 10.1 - Prob. 7TYCh. 10.1 - If a graph G has a Hamiltonian circuit, then G has...Ch. 10.1 - A travelling salesman problem involves finding a...Ch. 10.1 - In the graph below, determine whether the...
Ch. 10.1 - In the graph below, determine whether the...Ch. 10.1 - Let G be the graph and consider the walk...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - Consider the following graph. How many paths are...Ch. 10.1 - An edge whose removal disconnects the graph of...Ch. 10.1 - Given any positive integer n, (a) find a connected...Ch. 10.1 - Find the number of connected components for each...Ch. 10.1 - Each of (a)—(c) describes a graph. In each case...Ch. 10.1 - Prob. 10ESCh. 10.1 - Is it possible for a citizen of Königsberg to make...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Determine which of the graph in 12-17 have Euler...Ch. 10.1 - Is it possible to take a walk around the city...Ch. 10.1 - For each of the graph in 19-21, determine whether...Ch. 10.1 - Prob. 20ESCh. 10.1 - Prob. 21ESCh. 10.1 - Prob. 22ESCh. 10.1 - Prob. 23ESCh. 10.1 - Find the complement of each of the following...Ch. 10.1 - Find the complement of the graph K4, the complete...Ch. 10.1 - Suppose that in a group of five people A,B,C,D,...Ch. 10.1 - Prob. 27ESCh. 10.1 - Show that at a party with at least two people,...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Find Hamiltonian circuits for each of the graph in...Ch. 10.1 - Prob. 31ESCh. 10.1 - Show that none of graphs in 31-33 has a...Ch. 10.1 - Prob. 33ESCh. 10.1 - Prob. 34ESCh. 10.1 - Prob. 35ESCh. 10.1 - In 34-37, find Hamiltonian circuits for those...Ch. 10.1 - Prob. 37ESCh. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - Prob. 39ESCh. 10.1 - Prob. 40ESCh. 10.1 - Give two examples of graphs that have Euler...Ch. 10.1 - A traveler in Europe wants to visit each of the...Ch. 10.1 - a. Prove that if a walk in a graph contains a...Ch. 10.1 - Prob. 44ESCh. 10.1 - Prob. 45ESCh. 10.1 - Prob. 46ESCh. 10.1 - Prove that if there is a trail in a graph G from a...Ch. 10.1 - If a graph contains a circuits that starts and...Ch. 10.1 - Prob. 49ESCh. 10.1 - Let G be a connected graph, and let C be any...Ch. 10.1 - Prob. 51ESCh. 10.1 - Prob. 52ESCh. 10.1 - For what values of n dies the complete graph Kn...Ch. 10.1 - For what values of m and n does the complete...Ch. 10.1 - What is the maximum number of edges a simple...Ch. 10.1 - Prob. 56ESCh. 10.1 - Prob. 57ESCh. 10.2 - In the adjacency matrix for a directed graph, the...Ch. 10.2 - Prob. 2TYCh. 10.2 - Prob. 3TYCh. 10.2 - Prob. 4TYCh. 10.2 - Prob. 5TYCh. 10.2 - Prob. 6TYCh. 10.2 - Find real numbers a, b, and c such that the...Ch. 10.2 - Find the adjacency matrices for the following...Ch. 10.2 - Find directed graphs that have the following...Ch. 10.2 - Find adjacency matrices for the following...Ch. 10.2 - Find graphs that have the following adjacency...Ch. 10.2 - Prob. 6ESCh. 10.2 - Prob. 7ESCh. 10.2 - Prob. 8ESCh. 10.2 - Prob. 9ESCh. 10.2 - Prob. 10ESCh. 10.2 - Prob. 11ESCh. 10.2 - Prob. 12ESCh. 10.2 - Let O denote the matrix [0000] . Find 2 × 2...Ch. 10.2 - Prob. 14ESCh. 10.2 - Prob. 15ESCh. 10.2 - In 14-18, assume the entries of all matrices are...Ch. 10.2 - Prob. 17ESCh. 10.2 - Prob. 18ESCh. 10.2 - Prob. 19ESCh. 10.2 - The following is an adjacency matrix for a graph:...Ch. 10.2 - Let A be the adjacency matrix for K3, the complete...Ch. 10.2 - Draw a graph that has [0001200011000211120021100]...Ch. 10.2 - Prob. 23ESCh. 10.3 - If G and G’ are graphs, then G is isomorphic to G’...Ch. 10.3 - A property P is an invariant for graph isomorphism...Ch. 10.3 - Prob. 3TYCh. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 1-5, determine...Ch. 10.3 - For each pair of graphs G and G in 1—5, determine...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Prob. 9ESCh. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - For each pair of simple graphs G and G in 6—13,...Ch. 10.3 - For each pair of graphs G and G’ in 6-13,...Ch. 10.3 - Draw all nonisomorphic simple graphs with three...Ch. 10.3 - Draw all nonisomorphic simple graphs with four...Ch. 10.3 - Prob. 16ESCh. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Draw all nonisomorphic graphs with four vertices...Ch. 10.3 - Prob. 19ESCh. 10.3 - Draw four nonisomorphic graphs with six vertices,...Ch. 10.3 - Prob. 21ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 23ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 25ESCh. 10.3 - Prob. 26ESCh. 10.3 - Prob. 27ESCh. 10.3 - Prove that each of the properties in 21-29 is an...Ch. 10.3 - Prob. 29ESCh. 10.3 - Show that the following two graphs are not...Ch. 10.4 - A circuit-free graph is a graph with __________.Ch. 10.4 - Prob. 2TYCh. 10.4 - Prob. 3TYCh. 10.4 - Prob. 4TYCh. 10.4 - Prob. 5TYCh. 10.4 - Prob. 6TYCh. 10.4 - For any positive integer n, if G is a connected...Ch. 10.4 - Read the tree in Example 10.4.2 from left to right...Ch. 10.4 - Prob. 2ESCh. 10.4 - Prob. 3ESCh. 10.4 - Prob. 4ESCh. 10.4 - Prob. 5ESCh. 10.4 - Prob. 6ESCh. 10.4 - Prob. 7ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - Prob. 14ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - Prob. 17ESCh. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - In each of 8—21, either draw a graph with the...Ch. 10.4 - A connected graph has twelve vertices and eleven...Ch. 10.4 - A connected graph has nine vertices and twelve...Ch. 10.4 - Prob. 24ESCh. 10.4 - Prob. 25ESCh. 10.4 - If a graph has n vertices and n2 or fewer can it...Ch. 10.4 - A circuit-free graph has ten vertices and nine...Ch. 10.4 - Is a circuit-free graph with n vertices and at...Ch. 10.4 - Prob. 29ESCh. 10.4 - Prob. 30ESCh. 10.4 - a. Prove that the following is an invariant for...Ch. 10.5 - Prob. 1TYCh. 10.5 - Prob. 2TYCh. 10.5 - Prob. 3TYCh. 10.5 - Prob. 4TYCh. 10.5 - Prob. 5TYCh. 10.5 - Prob. 1ESCh. 10.5 - Prob. 2ESCh. 10.5 - Draw binary trees to represent the following...Ch. 10.5 - Prob. 4ESCh. 10.5 - Prob. 5ESCh. 10.5 - Prob. 6ESCh. 10.5 - Prob. 7ESCh. 10.5 - Prob. 8ESCh. 10.5 - Prob. 9ESCh. 10.5 - Prob. 10ESCh. 10.5 - Prob. 11ESCh. 10.5 - Prob. 12ESCh. 10.5 - Prob. 13ESCh. 10.5 - Prob. 14ESCh. 10.5 - Prob. 15ESCh. 10.5 - Prob. 16ESCh. 10.5 - Prob. 17ESCh. 10.5 - Prob. 18ESCh. 10.5 - Prob. 19ESCh. 10.5 - Prob. 20ESCh. 10.5 - Prob. 21ESCh. 10.5 - Prob. 22ESCh. 10.5 - Prob. 23ESCh. 10.5 - Prob. 24ESCh. 10.5 - In 21-25, use the steps of Algorithm 10.5.1 to...Ch. 10.6 - Prob. 1TYCh. 10.6 - Prob. 2TYCh. 10.6 - Prob. 3TYCh. 10.6 - In Kruskal’s algorithm, the edges of a connected,...Ch. 10.6 - Prob. 5TYCh. 10.6 - Prob. 6TYCh. 10.6 - At each stage of Dijkstra’s algorithm, the vertex...Ch. 10.6 - Prob. 1ESCh. 10.6 - Prob. 2ESCh. 10.6 - Prob. 3ESCh. 10.6 - Prob. 4ESCh. 10.6 - Prob. 5ESCh. 10.6 - Prob. 6ESCh. 10.6 - Prob. 7ESCh. 10.6 - Prob. 8ESCh. 10.6 - Prob. 9ESCh. 10.6 - Prob. 10ESCh. 10.6 - A pipeline is to be built that will link six...Ch. 10.6 - Use Dijkstra’s algorithm for the airline route...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Use Dijkstra’s algorithm to find the shortest path...Ch. 10.6 - Prob. 17ESCh. 10.6 - Prob. 18ESCh. 10.6 - Prob. 19ESCh. 10.6 - Prob. 20ESCh. 10.6 - Prob. 21ESCh. 10.6 - Prob. 22ESCh. 10.6 - Prob. 23ESCh. 10.6 - Prob. 24ESCh. 10.6 - Prob. 25ESCh. 10.6 - Prob. 26ESCh. 10.6 - Prob. 27ESCh. 10.6 - Suppose a disconnected graph is input to Kruskal’s...Ch. 10.6 - Suppose a disconnected graph is input to Prim’s...Ch. 10.6 - Modify Algorithm 10.6.3 so that the output...Ch. 10.6 - Prob. 31ES
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- Assuming Get Food Now achieved 12,000 interactions, how many of these would have resulted in customer being less than satisfied with their first interaction?arrow_forwardGiven the number of rows = 5, dfWithin = 24, and alpha is set at .05, what is q when calculating Tukey's HSD for a row effect?arrow_forwardProve that Cay({(0, 1), (1, 1)}:Zm ⊕Zn) has a Hamiltonian circuitfor all m and n greater than 1.arrow_forward
- The lattice points (a, b) and (m, n) are mutually visible if and only if a and b - n are relatively prime.arrow_forwardAt which point should i place the receiver on this satelite?arrow_forwardCompany X has 10 employees, each placing an average of 20 minutes of long-distance calls per day. The average call lasts 5 minutes. It has been determined that 20% of the calls are made during busy hour. A total of 4 external phone lines are used to place the pool of calls. Calculate the traffic flow in Erlang during the busy hour.arrow_forward
- Find a Hamiltonian circuit in Cay({(1, 0), (0, 1)}:Z4 ⊕ Z6).arrow_forwardPlease study the following Activity on Network Diagram and answer the questions below: Identify the Critical Path from the above AON Diagram. Calculate all the total floats. Calculate all the free floats.arrow_forwardConsider one application in which either a first order or second order IVP is formed to find a solution in a model problem.arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
Graph Theory: Euler Paths and Euler Circuits; Author: Mathispower4u;https://www.youtube.com/watch?v=5M-m62qTR-s;License: Standard YouTube License, CC-BY
WALK,TRIAL,CIRCUIT,PATH,CYCLE IN GRAPH THEORY; Author: DIVVELA SRINIVASA RAO;https://www.youtube.com/watch?v=iYVltZtnAik;License: Standard YouTube License, CC-BY