
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 1.CR, Problem 38CR
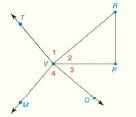
Fill in the missing statements or reasons.
| Given: |
|
| Prove: |
|
| Proof | |
| Statements | Reasons |
| 1.
|
1. Given |
| 2. ? | 2. Given |
| (1), (2) 3. ? | 3. Transitive Property of
|
| (3) 4.
|
4. ? |
| 5.
|
5. ? |
| 6. ? | 6. If a ray bisects an
|
| (4), (6), 7. ? | 7. Addition Property of Equality |
| 8.
|
8. ? |
| (7), (8) 9.
|
9. ? |
| 10. ? | 10. If two
|
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 1 Solutions
Elementary Geometry for College Students
Ch. 1.1 - In Exercises 1 and 2, which sentences are...Ch. 1.1 - In Exercises 1 and 2, which sentences are...Ch. 1.1 - In Exercises 3 and 4, give the negation of each...Ch. 1.1 - In Exercises 3 and 4, give the negation of each...Ch. 1.1 - In Exercises 5 to 10, classify each statement as...Ch. 1.1 - In Exercises 5 to 10, classify each statement as...Ch. 1.1 - In Exercises 5 to 10, classify each statement as...Ch. 1.1 - In Exercises 5 to 10, classify each statement as...Ch. 1.1 - In Exercises 5 to 10, classify each statement as...Ch. 1.1 - In Exercises 5 to 10, classify each statement as...
Ch. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - Prob. 14ECh. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - In Exercises 11 to 18, state the hypothesis and...Ch. 1.1 - In Exercises 19 to 24, classify each statement as...Ch. 1.1 - In Exercises 19 to 24, classify each statement as...Ch. 1.1 - In Exercises 19 to 24, classify each statement as...Ch. 1.1 - In Exercises 19 to 24, classify each statement as...Ch. 1.1 - In Exercises 19 to 24, classify each statement as...Ch. 1.1 - In Exercises 19 to 24, classify each statement as...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - In Exercises 25 to 32, name the type of reasoning...Ch. 1.1 - Prob. 32ECh. 1.1 - In Exercises 33 to 36, use intuition to state a...Ch. 1.1 - Prob. 34ECh. 1.1 - In Exercises 33 to 36, use intuition to state a...Ch. 1.1 - In Exercises 33 to 36, use intuition to state a...Ch. 1.1 - Prob. 37ECh. 1.1 - In Exercises 37 to 40, use induction to state a...Ch. 1.1 - Prob. 39ECh. 1.1 - In Exercises 37 to 40, use induction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - Prob. 47ECh. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 41 to 50, use deduction to state a...Ch. 1.1 - In Exercises 51 to 54, use Venn diagrams to...Ch. 1.1 - In Exercises 51 to 54, use Venn diagrams to...Ch. 1.1 - In Exercises 51 to 54, use Venn diagrams to...Ch. 1.1 - In Exercises 51 to 54, use Venn diagrams to...Ch. 1.1 - Prob. 55ECh. 1.1 - In Exercises 55 and 56, P is a true statement,...Ch. 1.1 - In Exercises 55 and 56, P is a true statement,...Ch. 1.2 - If line segment AB and line segment CD are drawn...Ch. 1.2 - If angles ABC and DEF were measured with a...Ch. 1.2 - How many endpoints does a line segment have? How...Ch. 1.2 - Do the points A, B, and C appear to be collinear?Ch. 1.2 - How many lines can be drawn that contain both...Ch. 1.2 - Consider noncollinear points A, B, and C. If each...Ch. 1.2 - Name all the angles in the figure.Ch. 1.2 - Which of the following measures can an angle have?...Ch. 1.2 - Must two different points be collinear? Must three...Ch. 1.2 - Which symbols correctly expresses the order in...Ch. 1.2 - Which symbols correctly name the angle shown?ABC,...Ch. 1.2 - A triangle is named ABC. Can it also be named ACB?...Ch. 1.2 - Consider rectangle MNQ. Can it also be named...Ch. 1.2 - Suppose ABC and DEF have the same measure. Which...Ch. 1.2 - Suppose AB and CD have the same length. Which...Ch. 1.2 - When two lines cross intersect, they have exactly...Ch. 1.2 - Judging from the ruler shown not to scale,...Ch. 1.2 - Judging from the ruler, estimate the measure of...Ch. 1.2 - Prob. 19ECh. 1.2 - Prob. 20ECh. 1.2 - Consider the square at the right, RSTV. It has...Ch. 1.2 - Square RSTV has diagonals RT and SV not shown. If...Ch. 1.2 - Use a compass to draw a circle. Draw a radius, a...Ch. 1.2 - Use a compass to draw a circle of radius 1 inch....Ch. 1.2 - The sides of the pair of angles are parallel. Are...Ch. 1.2 - The sides of the pair of angles are parallel. Are...Ch. 1.2 - The sides of the pair of angles are perpendicular....Ch. 1.2 - The sides of the pair of angles are perpendicular....Ch. 1.2 - On a piece of paper, use your compass to construct...Ch. 1.2 - On a piece of paper, use your protractor to draw a...Ch. 1.2 - A trapezoid is a four-sided figure that contains...Ch. 1.2 - In the rectangle shown, what is true of the...Ch. 1.2 - Prob. 33ECh. 1.2 - An angle is bisected if its two parts have the...Ch. 1.2 - Prob. 35ECh. 1.2 - Prob. 36ECh. 1.2 - Prob. 37ECh. 1.2 - Prob. 38ECh. 1.2 - ABC is straight angle. Using your protractor, you...Ch. 1.2 - Prob. 40ECh. 1.2 - Prob. 41ECh. 1.2 - In Exercises 41 to 44,m1+m2=mABC. Find m1 if...Ch. 1.2 - Prob. 43ECh. 1.2 - Prob. 44ECh. 1.2 - A compass was used to mark off three congruent...Ch. 1.2 - Use your compass and straightedge to bisect EF.Ch. 1.2 - In the figure, m1=x and m2=y. If x-y=24, find x...Ch. 1.2 - In the drawing, m1=x and m2=y. If mRSV=67 and...Ch. 1.2 - For Exercises 49 to 50, use the following...Ch. 1.2 - For Exercises 49 to 50, use the following...Ch. 1.3 - In Exercises 1 and 2, complete the statement....Ch. 1.3 - In Exercises 1 and 2, complete the statement....Ch. 1.3 - In Exercises 3 and 4, use the fact that...Ch. 1.3 - Prob. 4ECh. 1.3 - Prob. 5ECh. 1.3 - In Exercises 5 and 6, use the fact that...Ch. 1.3 - Prob. 7ECh. 1.3 - A cross-country runner jogs at a rate of 15 feet...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - Prob. 20ECh. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - Prob. 22ECh. 1.3 - Prob. 23ECh. 1.3 - Prob. 24ECh. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - Prob. 27ECh. 1.3 - In Exercises 9 to 28, use the drawings as needed...Ch. 1.3 - Prob. 29ECh. 1.3 - In Exercises 29 to 32, use only a compass and a...Ch. 1.3 - In Exercises 29 to 32, use only a compass and a...Ch. 1.3 - Prob. 32ECh. 1.3 - Can you use the construction for the midpoint of a...Ch. 1.3 - Generalize your findings in Exercise 33. 33. Can...Ch. 1.3 - Consider points A, B, C, and D, no three of which...Ch. 1.3 - Consider noncoplanar points A, B, C, and D. Using...Ch. 1.3 - Line l is parallel to plane P that is, it will not...Ch. 1.3 - AB and EF are said to be skew lines because they...Ch. 1.3 - Exercises 3840 In the box shown for Exercise 38,...Ch. 1.3 - Exercises 3940 In the box shown for Exercise 38,...Ch. 1.3 - Let AB=a and BC=b. Point M is the midpoint of BC....Ch. 1.4 - What type of angle has the given measure? a 47 b...Ch. 1.4 - What type of angle has the given measure? a 115 b...Ch. 1.4 - What relationship, if any, exists between two...Ch. 1.4 - What relationship, if any, exists between two...Ch. 1.4 - In Exercises 5 to 8, describe in one word the...Ch. 1.4 - In Exercises 5 to 8, describe in one word the...Ch. 1.4 - In Exercises 5 to 8, describe in one word the...Ch. 1.4 - In Exercises 5 to 8, describe in one word the...Ch. 1.4 - Use drawings as needed to answer each of the...Ch. 1.4 - Suppose that AB,AC,AD,AE, and AF are coplanar,...Ch. 1.4 - Exercises 10-13 Without using a protractor, name...Ch. 1.4 - Exercises 10-13 What, if anything, is wrong with...Ch. 1.4 - Exercises 10-13 FAC and CAD are adjacent and AF...Ch. 1.4 - For Exercises 14 and 15, let m1=x and m2=y. Using...Ch. 1.4 - For Exercises 14 and 15, let m1=x and m2=y. Using...Ch. 1.4 - Given: mRST=39 mTSV=23 Find: mRSV Exercises 1624Ch. 1.4 - Exercises 1624 Given: mRSV=59 mTSV=17 Find: mRSTCh. 1.4 - Exercises 1624 Given: mRST=2x+9 mTSV=3x2 mRSV=67...Ch. 1.4 - Exercises 1624 Given: mRST=2x10 mTSV=x+6...Ch. 1.4 - Exercises 1624 Given: mRST=5(x+1)3 mTSV=4(x2)+3...Ch. 1.4 - Exercises 1624 Given: mRST=x2 mTSV=x4 mRSV=45...Ch. 1.4 - Exercises 1624 Given: mRST=2x3 mTSV=x2 mRSV=49...Ch. 1.4 - Exercises 1624 Given: STbisectsRSV mRST=x+y...Ch. 1.4 - Exercises 1624 Given: STbisectsRSV mRST=2x+3y...Ch. 1.4 - Given: AB and AC in plane P as shown AD intersects...Ch. 1.4 - Two angles are complementary. One angle is 12...Ch. 1.4 - Two angles are supplementary. One angle is 24 more...Ch. 1.4 - For two complementary angles, find an expression...Ch. 1.4 - Suppose that the two angles are supplementary....Ch. 1.4 - On the protractor shown, NP bisects MNQ. Find x....Ch. 1.4 - Exercises 30,31 On the protractor shown for...Ch. 1.4 - Classify as true or false: a If points P and Q lie...Ch. 1.4 - Prob. 33ECh. 1.4 - Prob. 34ECh. 1.4 - In Exercises 33 to 40, use only a compass and a...Ch. 1.4 - Prob. 36ECh. 1.4 - Draw a triangle with three acute angles. Construct...Ch. 1.4 - Prob. 38ECh. 1.4 - Prob. 39ECh. 1.4 - Prob. 40ECh. 1.4 - Prob. 41ECh. 1.4 - If mTSV=38,mUSW=40, and mTSW=61, find mUSV....Ch. 1.4 - Exercises 44, 45 If mTSU=x+2z,mUSV=xz, and...Ch. 1.4 - Prob. 44ECh. 1.4 - Prob. 45ECh. 1.4 - With 0x90, an acute angle has a measure x. Find...Ch. 1.5 - In Exercises 1 to 6, which property justifies the...Ch. 1.5 - In Exercises 1 to 6, which property justifies the...Ch. 1.5 - In Exercises 1 to 6, which property justifies the...Ch. 1.5 - Prob. 4ECh. 1.5 - Prob. 5ECh. 1.5 - In Exercises 1 to 6, which property justifies the...Ch. 1.5 - In Exercises 7 10, state the property or...Ch. 1.5 - In Exercises 7 10, state the property or...Ch. 1.5 - Prob. 9ECh. 1.5 - In Exercises 7 10, state the property or...Ch. 1.5 - Prob. 11ECh. 1.5 - Prob. 12ECh. 1.5 - Prob. 13ECh. 1.5 - Prob. 14ECh. 1.5 - Prob. 15ECh. 1.5 - Prob. 16ECh. 1.5 - In Exercises 11 to 22, use the Given information...Ch. 1.5 - Prob. 18ECh. 1.5 - Prob. 19ECh. 1.5 - Prob. 20ECh. 1.5 - In Exercises 11 to 22, use the Given information...Ch. 1.5 - Prob. 22ECh. 1.5 - In Exercises 23 to 24, fill in the missing reasons...Ch. 1.5 - In Exercises 23 to 24, fill in the missing reasons...Ch. 1.5 - Prob. 25ECh. 1.5 - Prob. 26ECh. 1.5 - Prob. 27ECh. 1.5 - In Exercises 27 to 30, fill in the missing reasons...Ch. 1.5 - In Exercises 27 to 30, fill in the missing reasons...Ch. 1.5 - In Exercises 27 to 30, fill in the missing reasons...Ch. 1.5 - In Exercises 31 and 32, fill in the missing...Ch. 1.5 - In Exercises 31 and 32, fill in the missing...Ch. 1.5 - Prob. 33ECh. 1.5 - Prob. 34ECh. 1.5 - Prob. 35ECh. 1.5 - The Division Property of Inequality requires that...Ch. 1.5 - Prob. 37ECh. 1.5 - Write a proof for: If a=b and c=d, then ac=bd....Ch. 1.6 - In Exercise 1 and 2, supply reasons. Given: 13...Ch. 1.6 - In Exercise 1 and 2, supply reasons. Given: AB...Ch. 1.6 - In Exercise 3 and 4, supply statements. Given: 12...Ch. 1.6 - In Exercise 3 and 4, supply statements. Given:...Ch. 1.6 - In Exercise 5 to 9, use a compass and a...Ch. 1.6 - In Exercises 5 to 9, use a compass and a...Ch. 1.6 - In Exercise 5 to 9, use a compass and a...Ch. 1.6 - Prob. 8ECh. 1.6 - Prob. 9ECh. 1.6 - Prob. 10ECh. 1.6 - In Exercise 11 and 12, provide the missing...Ch. 1.6 - In Exercise 11 and 12, provide the missing...Ch. 1.6 - Does the relation is perpendicular to have a...Ch. 1.6 - Does the relation is greater than have a reflexive...Ch. 1.6 - Does the relation is complementary to for angles...Ch. 1.6 - Does the relation is less than for a numbers have...Ch. 1.6 - Does the relation is a brother of have a reflexive...Ch. 1.6 - Does the relation is in love with have a reflexive...Ch. 1.6 - Prob. 19ECh. 1.6 - Prob. 20ECh. 1.6 - Prob. 21ECh. 1.6 - Prob. 22ECh. 1.6 - Prove the Extended Segment Addition Property by...Ch. 1.6 - The Segment-Addition Postulate can be generalized...Ch. 1.6 - Prove the Extended Angle Addition Property by...Ch. 1.6 - The Angle-Addition Postulate can be generalized as...Ch. 1.6 - Prob. 27ECh. 1.6 - In the proof below, provide the missing reasons....Ch. 1.6 - Prob. 29ECh. 1.6 - Prob. 30ECh. 1.7 - In Exercises 1 to 6, state the hypothesis H and...Ch. 1.7 - In Exercises 1 to 6, state the hypothesis H and...Ch. 1.7 - In Exercises 1 to 6, state the hypothesis H and...Ch. 1.7 - In Exercises 1 to 6, state the hypothesis H and...Ch. 1.7 - Prob. 5ECh. 1.7 - In Exercises 1 to 6, state the hypothesis H and...Ch. 1.7 - Name, in order, the five parts of the formal proof...Ch. 1.7 - Which part hypothesis or conclusion of a theorem...Ch. 1.7 - Which part Given or Prove of the proof depends...Ch. 1.7 - Which of the following can be cited as a reason in...Ch. 1.7 - When can a theorem be cited as a reason reason in...Ch. 1.7 - Based upon the hypothesis of a theorem, do the...Ch. 1.7 - Prob. 13ECh. 1.7 - Prob. 14ECh. 1.7 - For each theorem stated in Exercises 13 to 18,...Ch. 1.7 - Prob. 16ECh. 1.7 - For each theorem stated in Exercises 13 to 18,...Ch. 1.7 - Prob. 18ECh. 1.7 - Prob. 19ECh. 1.7 - Prob. 20ECh. 1.7 - Prob. 21ECh. 1.7 - Prob. 22ECh. 1.7 - Prob. 23ECh. 1.7 - Prob. 24ECh. 1.7 - In Exercises 19 to 26, use the drawing in which AC...Ch. 1.7 - In Exercises 19 to 26, use the drawing in which AC...Ch. 1.7 - Prob. 27ECh. 1.7 - Prob. 28ECh. 1.7 - In Exercises 27 to 35, complete the formal proof...Ch. 1.7 - Prob. 30ECh. 1.7 - Prob. 31ECh. 1.7 - Prob. 32ECh. 1.7 - In Exercises 27 to 35, complete the formal proof...Ch. 1.7 - In Exercises 27 to 35, complete the formal proof...Ch. 1.7 - In Exercises 27 to 35, complete the formal proof...Ch. 1.CR - Name the four components of a mathematical system.Ch. 1.CR - Name three types of reasoning.Ch. 1.CR - Name the four characteristics of a good...Ch. 1.CR - In Review Exercises 4 to 6, name the type of...Ch. 1.CR - In Review Exercises 4 to 6, name the type of...Ch. 1.CR - In Review Exercises 4 to 6, name the type of...Ch. 1.CR - In Review Exercises 7 and 8, state the hypothesis...Ch. 1.CR - In Review Exercises 7 and 8, state the hypothesis...Ch. 1.CR - Prob. 9CRCh. 1.CR - Prob. 10CRCh. 1.CR - Prob. 11CRCh. 1.CR - A, B and C are three points on a line. AC=8, BC=4,...Ch. 1.CR - Use three letters to name the angle shown. Also...Ch. 1.CR - Figure MNPQ is a rhombus. Draw diagonals MP and QN...Ch. 1.CR - In Review Exercises 15 to 17, sketch and label the...Ch. 1.CR - In Review Exercises 15 to 17, sketch and label the...Ch. 1.CR - In Review Exercises 15 to 17, sketch and label the...Ch. 1.CR - On the basis of appearance, what type of angle is...Ch. 1.CR - On the basis of appearance, what type of angle is...Ch. 1.CR - Given: BD bisects ABC mABD=2x+15 mDBC=3x+5 Find:...Ch. 1.CR - Given: mABD=2x+5 mDBC=3x4 mABC=86 Find: mDBCCh. 1.CR - Given: AM=3x1 MB=4x5 M is the midpoint of AB Find:...Ch. 1.CR - Given: AM=4x4 MB=5x+2 AB=25 Find: MBCh. 1.CR - Given: D is the midpoint of AC ACBC CD=2x+5...Ch. 1.CR - Given: m3=7x21 m4=3x+7 Find: mFMHCh. 1.CR - Given: mFMH=4x+1 m4=x+4 Find: m4Ch. 1.CR - In the figure, find: a KHFJ b MJMH c KMJJMH d MKMHCh. 1.CR - Given: EFG is a right angle. mHFG=2x6 mEFH=3mHFG...Ch. 1.CR - Two angles are supplementary. One angle is 40 more...Ch. 1.CR - aWrite an expression for the perimeter of the...Ch. 1.CR - The sum of the measures of all three angles of the...Ch. 1.CR - Susan wants to have a 4-ft board with some pegs on...Ch. 1.CR - State whether the sentences in Review Exercises 33...Ch. 1.CR - State whether the sentences in Review Exercises 33...Ch. 1.CR - State whether the sentences in Review Exercises 33...Ch. 1.CR - State whether the sentences in Review Exercises 33...Ch. 1.CR - State whether the sentences in Review Exercises 33...Ch. 1.CR - Fill in the missing statements or reasons. Given:...Ch. 1.CR - Write two-column proofs for Review Exercises 39 to...Ch. 1.CR - Write two-column proofs for Review Exercises 39 to...Ch. 1.CR - Prob. 41CRCh. 1.CR - Prob. 42CRCh. 1.CR - Prob. 43CRCh. 1.CR - Prob. 44CRCh. 1.CR - Prob. 45CRCh. 1.CR - Prob. 46CRCh. 1.CR - Given: VP Construct: VW such that VW=4VPCh. 1.CR - Prob. 48CRCh. 1.CR - Prob. 49CRCh. 1.CR - Prob. 50CRCh. 1.CR - Prob. 51CRCh. 1.CR - Prob. 52CRCh. 1.CT - Which type of reasoning is illustrated...Ch. 1.CT - Given ABC as shown, provide a second correct...Ch. 1.CT - Using the Segment-Addition Postulate, state a...Ch. 1.CT - Complete each postulate: a If two lines intersect,...Ch. 1.CT - Prob. 5CTCh. 1.CT - Prob. 6CTCh. 1.CT - Given that NP bisects MNQ, state a conclusion...Ch. 1.CT - Complete each theorem: a If two lines are...Ch. 1.CT - State the conclusion for the following deductive...Ch. 1.CT - Prob. 10CTCh. 1.CT - In the figure, AB=x, BD=x+5, and AD=27. Find: a...Ch. 1.CT - Prob. 12CTCh. 1.CT - Prob. 13CTCh. 1.CT - Prob. 14CTCh. 1.CT - Prob. 15CTCh. 1.CT - Prob. 16CTCh. 1.CT - Prob. 17CTCh. 1.CT - Construct the angle bisector of obtuse angle RST.Ch. 1.CT - Prob. 19CTCh. 1.CT - In exercises 20 to 22, complete the missing...Ch. 1.CT - Prob. 21CTCh. 1.CT - In exercises 20 to 22, complete the missing...Ch. 1.CT - Prob. 23CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Given: l1l2l3,AB=5,BC=x,DE=x2,EF=7 Find: x,BC,DEarrow_forwardGiven: l1l2l3,AB=4,BC=5,DE=x,EF=12x Find: x,DE,EFarrow_forwardWhich of the following statements would you prove by the indirect method? a If ACAB in ABC, then mBmC. b If AC=AB in ABC, then mB=mC. c If RSTV is not a square, then RSST. d An angle has exactly one bisector.arrow_forward
- Complete all statements and reasons for the following proof problem. Given: R and V are right angles;12 Prove: RSTVST PROOF Statements Reasonsarrow_forwardReview Exercises Given: MNOP mM=4x mO=2x+50 Find: mMandmParrow_forwardSuppose that the two angles are supplementary. Find expressions for the supplements, using the expressions provided in Exercise 28, parts a to c. For two complementary angles, find an expression for the measure of the second angle if the measure of first is: a x b (3x12) c (2x+5v)arrow_forward
- The Angle-Addition Postulate can be generalized as follows: The measure of an angle equals the sum of measures of its parts. State a general conclusion regarding mGHK based on the figure shown.arrow_forwardIn Exercise 3 and 4, supply statements. Given: mAOBm1mBOCm1 Prove: OB bisects AOC PROOF Statements Reasons 1. ? 1. Given 2. ? 2. Substitution 3. ? 3. Angles with equal measures are congruent. 4. ? 4. If a ray divides an angle into two congruent angles, then the ray bisects the angle.arrow_forwardIn the figure, m1=x and m2=y. If x-y=24, find x and y. HINT: m1+m2=180.arrow_forward
- In Exercises 55 and 56, P is a true statement, while Q and R are false statements. Classify each of the following statements as true or false. a PandQorR b PorQandRarrow_forwardGiven: m1=x212 m4=x(x2) Find: x so that ABCDarrow_forwarda Which of these (AB,AB,orAB) represents the length of the line segment AB? b Which (mCBA, mCAB,or, mBAC) represents the measure of mABCarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Elementary Linear Algebra (MindTap Course List)
Algebra
ISBN:9781305658004
Author:Ron Larson
Publisher:Cengage Learning
Surface Area Of A Sphere | Geometry | Math | Letstute; Author: Let'stute;https://www.youtube.com/watch?v=T_DBkFnr4NM;License: Standard YouTube License, CC-BY