Chapter 20, Problem 15P

Human blood behaves as a Newtonian fluid (see Prob. 20.55) in the high shear rate region where $\stackrel{\dot{}}{\gamma }>100$.In the low shear rate region where $\stackrel{\dot{}}{\gamma }>50$, the red cells tend to aggregate into what are called rouleaux, which make the fluid behavior depart fromNewtonian. This low shear rate region is called the Casson region, and there is a transition region between the two distinct flow regions. In the Casson region as shear rate approaches zero, the shear stress goes to a finite value, similar to a Bingham plastic, which is called the yield stress, ${\tau }_y$, and this stress must be overcome in order to initiate flow in stagnate blood. Flow in the Casson region is usually plotted as the square root of shear rate versus the square root of shear stress, and follows a straight line relationship when plotted in this way. The Casson relationship is

$\sqrt{\tau }=\sqrt{{\tau }_y}+K_c\sqrt{\stackrel{\dot{}}{\gamma }}$

where $K_c=$ consistency index. In the table below are experimentally measured values of $\stackrel{\dot{}}{\gamma }$ and $\tau$ from a single blood sample over the Casson and Newtonian flow regions.

$\stackrel{\dot{}}{\gamma },1\text{/s}$	0.91	3.3	4.1	6.3	9.6	23	36	49	65	105	126	215	315	402
$\tau ,{\text{N/m}}^{\text{2}}$	0.059	0.15	0.19	0.27	0.39	0.87	1.33	1.65	2.11	3.44	4.12	7.02	10.21	13.01
Region	Casson	Transition	Newtonian

Find the values of $K_c$ and ${\tau }_y$ using linear regression in the Casson region, and find $\mu$ by using linear regression in the Newtonian region. Also find the correlation coefficient for each regression analysis. Plot the two regression lines on a Casson plot ( $\sqrt{\stackrel{\dot{}}{\gamma }}$ versus $\sqrt{\tau }$) and extend the regression lines as dashed lines into adjoining regions; also include the data points in the plot. Limit the shear rate region to $0<\sqrt{\stackrel{\dot{}}{\gamma }}<15$.

To determine

To calculate: The values of $K_c$ and ${\tau }_y$ using linear regression in the Casson region and find $\mu$ using linear regression in the Newtonian region using the following experimentally measured values of $\dot{\gamma }$ and $\tau$ from a single blood sample over the Casson and Newtonian flow regions,

$\dot{\gamma },\text{1/s}$	0.91	3.3	4.1	6.3	9.6	23	36	49	65	105	126	215	315	402
$\tau ,{\text{N/m}}^{\text{2}}$	0.0059	0.15	0.19	0.27	0.39	0.84	1.33	1.65	2.11	3.44	4.12	7.02	10.21	13.01
Region	Casson							Transition		Newtonian

Also, find the correlation coefficient for each regression analysis. Plot the two regression lines on the Casson plot ($\sqrt{\dot{\gamma }}$ versus $\sqrt{\tau }$

) and extend the regressions lines as dashed lines into adjoining regressions and include the given data points in the plots.

Answer to Problem 15P

Solution: In the Casson region $\underset{\_}{K_c=0.19754,{\tau }_y=0.00011}$

and in Newtonian region $\underset{\_}{\mu =0.53848}$. The correlation coefficients in the Casson region $\underset{\_}{r=0.98907}$

and in Newtonian region $\underset{\_}{r=0.78559}$.

Explanation of Solution

Given Information: Consider the experimentally measured values of $\dot{\gamma }$ and $\tau$ from a single blood sample over the Casson and Newtonian flow regions,

$\dot{\gamma },\text{1/s}$	0.91	3.3	4.1	6.3	9.6	23	36	49	65	105	126	215	315	402
$\tau ,{\text{N/m}}^{\text{2}}$	0.0059	0.15	0.19	0.27	0.39	0.84	1.33	1.65	2.11	3.44	4.12	7.02	10.21	13.01
Region	Casson							Transition		Newtonian

The Casson relationship is with $K_c$ being consistency index,

$\sqrt{\tau }=\sqrt{{\tau }_y}+K_c\sqrt{\dot{\gamma }}$

The relationship for the Newtonian fluid,

$\tau =\mu \sqrt{\dot{\gamma }}$

Formula used:

If $y=a_0+a_{1}x$ be the linear regression for a set of $n$

data points $x_i,y_i,i=1,2,\mathrm{...},n$ then,

$a_1=\frac{n{\displaystyle \sum x_i{y}_i}-{\displaystyle \sum x_i}{\displaystyle \sum y_i}}{n{\displaystyle \sum x_i^2-{\left({\displaystyle \sum x_i}\right)}^2}};a_0=\overline{y}-a_1\overline{x}$

Here,

$\overline{x}=\frac{1}{n}{\displaystyle \sum x_i};\overline{y}=\frac{1}{n}{\displaystyle \sum y_i}$

If $y=a_{1}x$ be the linear regression for a set of $n$

data points $x_i,y_i,i=1,2,\mathrm{...},n$ then,

$a_1=\frac{{\displaystyle \sum x_i{y}_i}}{{\displaystyle \sum x_i^2}}$

The correlation coefficient is,

$r^2=\frac{s_t-s_r}{s_t};s_t={\displaystyle \sum {\left(Y_i-\overline{y}\right)}^2},s_r={\displaystyle \sum {\left(Y_i-\widehat{Y}\right)}^2}$

Here, $\widehat{Y}$ is the predicted value based on the regression fit.

Calculation:

Consider the experimentally measured values of $\dot{\gamma }$ and $\tau$ from a single blood sample over the Casson and Newtonian flow regions,

$\dot{\gamma },\text{1/s}$	0.91	3.3	4.1	6.3	9.6	23	36	49	65	105	126	215	315	402
$\tau ,{\text{N/m}}^{\text{2}}$	0.0059	0.15	0.19	0.27	0.39	0.84	1.33	1.65	2.11	3.44	4.12	7.02	10.21	13.01
Region	Casson							Transition		Newtonian

The Casson relationship is with $K_c$ being consistency index,

$\sqrt{\tau }=\sqrt{{\tau }_y}+K_c\sqrt{\dot{\gamma }}$

Defining the two variables $Y=\sqrt{\tau },X=\sqrt{\dot{\gamma }}$,

$Y=\sqrt{{\tau }_y}+K_{c}X$

Therefore, the unknown constant $\sqrt{{\tau }_y},K_c$ can be obtained using linear regressions,

$K_c=\frac{n{\displaystyle \sum X_i{Y}_i}-{\displaystyle \sum X_i}{\displaystyle \sum Y_i}}{n{\displaystyle \sum X_i^2-{\left({\displaystyle \sum X_i}\right)}^2}}$

$\sqrt{{\tau }_y}={\overline{Y}}_i-K_c{\overline{X}}_i$

Construct the following table considering the data in the Casson regions to compute the unknown constant $\sqrt{{\tau }_y},K_c$

$i$	${\dot{\gamma }}_i$	${\tau }_i$	$X_i=\sqrt{{\dot{\gamma }}_i}$	$Y_i=\sqrt{{\tau }_i}$	$X_i^2$	$X_i{Y}_i$
1	0.91	0.0059	0.95394	0.07681	0.91000	0.07327
2	3.3	0.15	1.81659	0.38730	3.30000	0.70356
3	4.1	0.19	2.02485	0.43589	4.10000	0.88261
4	6.3	0.27	2.50998	0.51962	6.30000	1.30422
5	9.6	0.39	3.09839	0.62450	9.60000	1.93494
6	23	0.84	4.79583	0.91652	23.00000	4.39545
7	36	1.33	6.00000	1.15326	36.00000	6.91954
${\displaystyle \sum }$			21.19957	4.11389	83.21000	16.21360

Therefore, the unknown constant $\sqrt{{\tau }_y},K_c$ using regression coefficients with $n=7$,

$\begin{array}{c}{K}_c=\frac{7\times 16.21360-21.19957\times 4.11389}{7\times 83.21-{\left(21.19957\right)}^2}\\ =0.19754\end{array}$

$\begin{array}{c}\overline{x}=\frac{21.19957}{7}\\ =3.02851\end{array}$

$\begin{array}{c}\overline{y}=\frac{4.11389}{7}\\ =0.58770\end{array}$

$\begin{array}{c}\sqrt{{\tau }_y}=0.58770-0.19754\times 3.02851\\ =-0.01055\end{array}$

Therefore,

$\begin{array}{c}{K}_c=0.19754\\ {\tau }_y=0.00011\end{array}$

Hence, the linear regression line for Casson region is,

$Y=-0.01055+0.19754X$

Construct the table to calculate the correlation coefficients defining ${\widehat{Y}}_i=-0.01055+0.19754X_i$

$i$	$X_i$	$Y_i$	${\left(Y_i-\overline{y}\right)}^2$	${\widehat{Y}}_i$	${\left(Y_i-{\widehat{Y}}_i\right)}^2$
1	0.95394	0.07681	0.26101	0.17789	0.01022
2	1.81659	0.38730	0.04016	0.34830	0.00152
3	2.02485	0.43589	0.02305	0.38944	0.00216
4	2.50998	0.51962	0.00463	0.48527	0.00118
5	3.09839	0.62450	0.00135	0.60151	0.00053
6	4.79583	0.91652	0.10812	0.93682	0.00041
7	6.00000	1.15326	0.31986	1.17469	0.00046
	${\displaystyle \sum }$		0.75818		0.01648

Therefore,

$s_t=0.75818,s_r=0.01648$

Hence, the correlation coefficients,

$\begin{array}{c}r=\sqrt{\frac{0.75818-0.01648}{0.75818}}\\ =0.98907\end{array}$

Therefore, for Casson region the linear fit is,

$\sqrt{\tau }=-0.01055+0.19754\sqrt{\dot{\gamma }}$ with $K_c=0.19754,{\tau }_y=0.00011$

And the correlation coefficients,

$r=0.98907$

Consider the Newtonian relationship as,

$\tau =\mu \dot{\gamma }$

From the linear regression,

$\mu =\frac{{\displaystyle \sum {\dot{\gamma }}_i{\tau }_i}}{{\displaystyle \sum {\dot{\gamma }}_i^2}}$

Construct the following table considering the data in the Newton regions to compute the unknown constant $\mu$

$i$	${\dot{\gamma }}_i$	${\tau }_i$	${\dot{\gamma }}_i^2$	$Y_i{\tau }_i$
1	105	3.44	11025	361.20
2	126	4.12	15876	519.12
3	215	7.02	46225	1509.30
4	315	10.21	99225	3216.15
5	402	13.01	161604	5230.02
${\displaystyle \sum }$		37.8	333955	10835.79

Therefore, the unknown constant $\mu$ using regression coefficients with $n=5$ is calculated as,

$\begin{array}{c}\mu =\frac{10835.79}{333955}\\ =0.03245\end{array}$

$\begin{array}{c}\overline{\tau }=\frac{37.8}{5}\\ =7.56\end{array}$

Therefore,

$\mu =0.03245$

Hence, the linear regression line for Newtonian region is,

$\tau =0.03245\dot{\gamma }$

Construct the table to calculate the correlation coefficients defining $\widehat{\tau }=0.03245\dot{\gamma }$

$i$	${\dot{\gamma }}_i$	${\tau }_i$	${\left({\tau }_i-\overline{\tau }\right)}^2$	${\widehat{\tau }}_i$	${\left({\tau }_i-{\widehat{\tau }}_i\right)}^2$
1	105	3.44	16.97440	3.40725	0.00107
2	126	4.12	16.97440	4.08870	0.00098
3	215	7.02	49.28040	6.97675	0.00187
4	315	10.21	104.24410	10.22175	0.00014
5	402	13.01	169.26010	13.04490	0.00122
	${\displaystyle \sum }$		356.73340		0.00528

Therefore,

$s_t=356.73340,s_r=0.00528$

Hence, the correlation coefficients,

$\begin{array}{c}r=\sqrt{\frac{356.73340-0.00528}{356.73340}}\\ =0.99999\end{array}$

Therefore, for Newtonian region the linear fit is

$\tau =0.03245\dot{\gamma }$ with $\mu =0.03245$

And the correlation coefficients,

$r=0.99999$

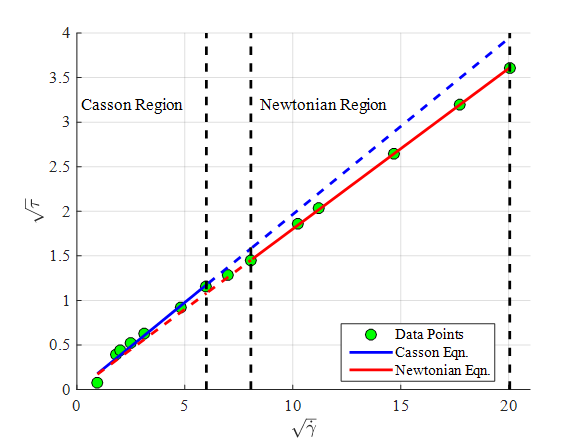
Graph:

Consider the two regression lines in the field of $\left(\sqrt{\tau },\sqrt{\dot{\gamma }}\right)$,

In the Casson region,

$\sqrt{\tau }=-0.01055+0.19754\sqrt{\dot{\gamma }}$

In the Newtonian region, $\sqrt{\tau }=\sqrt{0.03245}\sqrt{\dot{\gamma }}$

Construct the MATLAB function ‘Code_97924_20_15a.m’ to plot the two regression lines on the Casson plot ($\sqrt{\dot{\gamma }}$ versus $\sqrt{\tau }$

) and extend the regressions lines as dashed lines into adjoining regressions and include the given data points in the plots.

clear;clc;

% enter given data

Gama_dot = [0.91 3.3 4.1 6.3 9.6 23 36 49 65 105 126 215 315 402];

Tau = [0.0059 0.15 0.19 0.27 0.39 0.84 1.33 1.65 2.11 3.44 4.12 7.02 10.21 13.01];

%– Casson Region: Regression Line

Yc = @(X) -0.01055 + 0.19754*X;

%– Newtonian Region: Regression Line

Yn = @(X) sqrt(0.03245)*X;

% define the range

Xc = sqrt(linspace(0.91, 36, 20));

Xt = sqrt(linspace(37, 65, 20));

Xn = sqrt(linspace(66, 402, 50));

% generate the plot

figure(); hold on

plot(sqrt(Gama_dot), sqrt(Tau), 'o','MarkerEdgeColor','k',...

'MarkerFaceColor','g','MarkerSize',8);

% define graphical properties

plot(Xc, Yc(Xc), '-b' ,'linewidth',2);

plot(Xn, Yn(Xn), 'r','linewidth',2);

plot(Xt, Yc(Xt), '–b','linewidth',2);

plot(Xn, Yc(Xn), '–b','linewidth',2);

plot(Xc, Yn(Xc), '–r' ,'linewidth',2);

plot(Xt, Yn(Xt), '–r','linewidth',2);

% draw straight lines

h(1) = line(sqrt([36 36]) ,[0 5]);

h(2) = line(sqrt([65 65]) ,[0 5]);

h(3) = line(sqrt([402 402]),[0 5]);

t(1) = text(0.2,3.2,'Casson Region');

t(2) = text(8.5,3.2,'Newtonian Region');

xlim([0 21]); ylim([0 4]);grid on

legend('Data Points','Casson Eqn.', 'Newtonian Eqn.')

xlabel('$\sqrt{\dot{\gamma}}$','Interpreter','latex');

ylabel('$\sqrt{\tau}$','Interpreter','latex');

% define graphical properties

set(gca,'FontName','Times New Roman','FontSize',12);

set(h,'LineStyle','–','linewidth',2,'Color',[0 0 0])

set(t,'FontName','Times New Roman','FontSize',12);

The comparison is shown on the plot as,