
Finite Mathematics and Applied Calculus (MindTap Course List)
7th Edition
ISBN: 9781337274203
Author: Stefan Waner, Steven Costenoble
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 2.4, Problem 12E
To determine
The correct logistic function
from the given choices for the following curve,
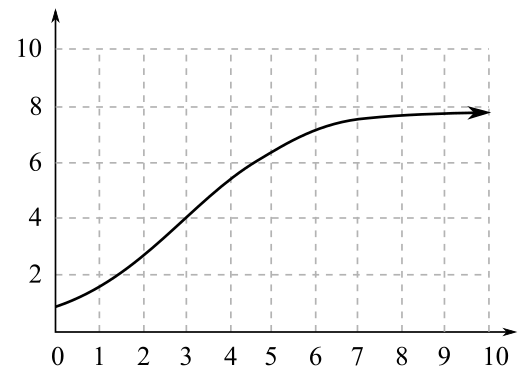
(A).
(B).
(C).
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Prove that the straight line y=3-2x intersects the exponential curve y=e^x at a point whose x-coordinate belongs to the interval (0,1).
In Exercises, sketch the shifted exponential curves
y = 2x - 1 and y = 2-x - 1
Suppose a new magazine initially sells 600 copies per month. Research indicates that a vigorous advertising campaign could increase sales by 40% each month if our market were unlimited. But research also indicates that magazine sales in our area are unlikely to exceed 2400 per month. Make a logistic model of projected magazine sales.
a) N = 600 / 1+3e^-0.336t
b) N = 2400 / 1+3e^-0.336t
c) N = 40 / 1+3e^-0.336t
d) N = 2400 / 1+40e^-0.336t
Chapter 2 Solutions
Finite Mathematics and Applied Calculus (MindTap Course List)
Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - In Exercises 16, (a) state the values of a, b, and...Ch. 2.1 - Prob. 6ECh. 2.1 - Prob. 7ECh. 2.1 - Prob. 8ECh. 2.1 - In Exercises 716, sketch the graph of the...Ch. 2.1 - Prob. 10E
Ch. 2.1 - Prob. 11ECh. 2.1 - In Exercises 716, sketch the graph of the...Ch. 2.1 - In Exercises 716, sketch the graph of the...Ch. 2.1 - Prob. 14ECh. 2.1 - Prob. 15ECh. 2.1 - Prob. 16ECh. 2.1 - In Exercises 1720, for each demand equation,...Ch. 2.1 - Prob. 18ECh. 2.1 - Prob. 19ECh. 2.1 - Prob. 20ECh. 2.1 - Prob. 21ECh. 2.1 - In Exercises 2124, use technology to find the...Ch. 2.1 - Prob. 23ECh. 2.1 - In Exercises 2124, use technology to find the...Ch. 2.1 - World Military Expenditure The following chart...Ch. 2.1 - Education Expenditure The following chart shows...Ch. 2.1 - Oil Imports from Mexico Crude oil imports to the...Ch. 2.1 - Oil Production in Mexico Crude oil production by...Ch. 2.1 - GE Net Income 20092013 The annual net income of...Ch. 2.1 - GE Net Income 20072011 The annual net income of...Ch. 2.1 - Revenue The market research department of the...Ch. 2.1 - Prob. 32ECh. 2.1 - Revenue Pack-Em-In Real Estate is building a new...Ch. 2.1 - Revenue Pack-Em-In has another development in the...Ch. 2.1 - Revenue from Monorail Service, Las Vegas In 2005...Ch. 2.1 - Revenue from Monorail Service, Mars The Utarek...Ch. 2.1 - Website Profit You operate a gaming website,...Ch. 2.1 - T-Shirt Profit Two fraternities, Sig Ep and Ep...Ch. 2.1 - Website Profit The latest demand equation for your...Ch. 2.1 - T-Shirt Profit The latest demand equation for your...Ch. 2.1 - Nightclub Management You have just opened a new...Ch. 2.1 - Television Advertising As sales manager for...Ch. 2.1 - Prob. 43ECh. 2.1 - Prob. 44ECh. 2.1 - iPod Sales The following table shows Apple iPod...Ch. 2.1 - iPod Sales The following table shows Apple iPod...Ch. 2.1 - What can you say about the graph of f(x)=ax2+bx+c...Ch. 2.1 - Prob. 48ECh. 2.1 - Multiple choice: Following is the graph of...Ch. 2.1 - Prob. 50ECh. 2.1 - Prob. 51ECh. 2.1 - Prob. 52ECh. 2.1 - Prob. 53ECh. 2.1 - Prob. 54ECh. 2.1 - Prob. 55ECh. 2.1 - Prob. 56ECh. 2.1 - Prob. 57ECh. 2.1 - Prob. 58ECh. 2.1 - Prob. 59ECh. 2.1 - Prob. 60ECh. 2.1 - If the revenue function for a particular commodity...Ch. 2.1 - If the revenue function for a particular commodity...Ch. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - Prob. 4ECh. 2.2 - Prob. 5ECh. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - Prob. 7ECh. 2.2 - Prob. 8ECh. 2.2 - Prob. 9ECh. 2.2 - Prob. 10ECh. 2.2 - In Exercises 1-12, compute the missing values in...Ch. 2.2 - Prob. 12ECh. 2.2 - In Exercises 13-18, graph the given function using...Ch. 2.2 - Prob. 14ECh. 2.2 - Prob. 15ECh. 2.2 - In Exercises 13-18, graph the given function using...Ch. 2.2 - Prob. 17ECh. 2.2 - In Exercises 13-18, graph the given function using...Ch. 2.2 - In Exercises 19-24 the values of two functions, f...Ch. 2.2 - Prob. 20ECh. 2.2 - Prob. 21ECh. 2.2 - Prob. 22ECh. 2.2 - Prob. 23ECh. 2.2 - Prob. 24ECh. 2.2 - In Exercises 25-30, supply a valid technology...Ch. 2.2 - Prob. 26ECh. 2.2 - Prob. 27ECh. 2.2 - Prob. 28ECh. 2.2 - In Exercises 25-30, supply a valid technology...Ch. 2.2 - In Exercises 25-30, supply a valid technology...Ch. 2.2 - Prob. 31ECh. 2.2 - Prob. 32ECh. 2.2 - Prob. 33ECh. 2.2 - Prob. 34ECh. 2.2 - Prob. 35ECh. 2.2 - Prob. 36ECh. 2.2 - Prob. 37ECh. 2.2 - Prob. 38ECh. 2.2 - Prob. 39ECh. 2.2 - Prob. 40ECh. 2.2 - Prob. 41ECh. 2.2 - Prob. 42ECh. 2.2 - Prob. 43ECh. 2.2 - Prob. 44ECh. 2.2 - Prob. 45ECh. 2.2 - Prob. 46ECh. 2.2 - In Exercises 47-54, model the data using an...Ch. 2.2 - Prob. 48ECh. 2.2 - Prob. 49ECh. 2.2 - Prob. 50ECh. 2.2 - In Exercises 47-54, model the data using an...Ch. 2.2 - Prob. 52ECh. 2.2 - In Exercises 47-54, model the data using an...Ch. 2.2 - Prob. 54ECh. 2.2 - Prob. 55ECh. 2.2 - Prob. 56ECh. 2.2 - In Exercises 55-62, find an equation for an...Ch. 2.2 - Prob. 58ECh. 2.2 - In Exercises 55-62, find an equation for an...Ch. 2.2 - In Exercises 55-62, find an equation for an...Ch. 2.2 - Prob. 61ECh. 2.2 - Prob. 62ECh. 2.2 - In Exercises 63-66, obtain an exponential function...Ch. 2.2 - Prob. 64ECh. 2.2 - In Exercises 63-66, obtain an exponential function...Ch. 2.2 - Prob. 66ECh. 2.2 - Prob. 67ECh. 2.2 - Prob. 68ECh. 2.2 - In Exercises 67-70, use technology to find the...Ch. 2.2 - Prob. 70ECh. 2.2 - Aspirin Soon after taking an aspirin, a patient...Ch. 2.2 - Alcohol After a large number of drinks, a person...Ch. 2.2 - Prob. 73ECh. 2.2 - Revenue The annual revenue of Amazon rose from...Ch. 2.2 - Prob. 75ECh. 2.2 - Prob. 76ECh. 2.2 - Prob. 77ECh. 2.2 - Prob. 78ECh. 2.2 - Bacteria A bacteria culture starts with 1,000...Ch. 2.2 - Prob. 80ECh. 2.2 - Prob. 81ECh. 2.2 - The 2003 SARS Outbreak A few weeks into the deadly...Ch. 2.2 - The 2014 Ebola Outbreak In the first six months of...Ch. 2.2 - Prob. 84ECh. 2.2 - Investments In August 2013, E*TRADE Financial was...Ch. 2.2 - Investments In August 2013, Ally Bank was offering...Ch. 2.2 - Prob. 87ECh. 2.2 - Prob. 88ECh. 2.2 - Investments Rock Solid Bank Trust is offering a...Ch. 2.2 - Savings FlybynightSavings.com is offering a...Ch. 2.2 - Prob. 91ECh. 2.2 - Home Prices The median selling price of an...Ch. 2.2 - Climate Change The most abundant greenhouse gas is...Ch. 2.2 - Prob. 94ECh. 2.2 - New York City Housing Costs: Downtown The...Ch. 2.2 - New York City Housing Costs: Uptown The following...Ch. 2.2 - Facebook The following table gives the approximate...Ch. 2.2 - Prob. 98ECh. 2.2 - Prob. 99ECh. 2.2 - Prob. 100ECh. 2.2 - Prob. 101ECh. 2.2 - Prob. 102ECh. 2.2 - Prob. 103ECh. 2.2 - Prob. 104ECh. 2.2 - Prob. 105ECh. 2.2 - Describe a real-life situation in which a...Ch. 2.2 - Prob. 107ECh. 2.2 - Prob. 108ECh. 2.2 - Prob. 109ECh. 2.2 - Prob. 110ECh. 2.3 - If y=4x, then x=.Ch. 2.3 - If y=log6x, then x=.Ch. 2.3 - Simplify: 2log28.Ch. 2.3 - Prob. 4ECh. 2.3 - Simplify: ln(ex).Ch. 2.3 - Simplify: lna.Ch. 2.3 - In Exercises 7-14, graph the given function....Ch. 2.3 - Prob. 8ECh. 2.3 - In Exercises 7-14, graph the given function....Ch. 2.3 - Prob. 10ECh. 2.3 - In Exercises 7-14, graph the given function....Ch. 2.3 - Prob. 12ECh. 2.3 - Prob. 13ECh. 2.3 - Prob. 14ECh. 2.3 - In Exercises 15-20, find the associated...Ch. 2.3 - Prob. 16ECh. 2.3 - Prob. 17ECh. 2.3 - Prob. 18ECh. 2.3 - In Exercises 15-20, find the associated...Ch. 2.3 - Prob. 20ECh. 2.3 - In Exercises 21-26, find the associated half-life...Ch. 2.3 - Prob. 22ECh. 2.3 - Prob. 23ECh. 2.3 - Prob. 24ECh. 2.3 - In Exercises 21-26, find the associated half-life...Ch. 2.3 - Prob. 26ECh. 2.3 - In Exercises 27-32, convert the given exponential...Ch. 2.3 - Prob. 28ECh. 2.3 - In Exercises 27-32, convert the given exponential...Ch. 2.3 - Prob. 30ECh. 2.3 - In Exercises 27-32, convert the given exponential...Ch. 2.3 - Prob. 32ECh. 2.3 - Investments How long will it take a $500...Ch. 2.3 - Prob. 34ECh. 2.3 - Investments How long, to the nearest year, will it...Ch. 2.3 - Investments How long, to the nearest year, will it...Ch. 2.3 - Prob. 37ECh. 2.3 - Depreciation My investment in OHaganBooks.com...Ch. 2.3 - Carbon Dating The amount of carbon 14 remaining in...Ch. 2.3 - Carbon Dating Refer to Exercise 39. How old, to...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Long-Term Investments Exercises 41-48 are based on...Ch. 2.3 - Prob. 47ECh. 2.3 - Prob. 48ECh. 2.3 - Half-Life The amount of radium 226 remaining in a...Ch. 2.3 - Half-Life The amount of iodine 131 remaining in a...Ch. 2.3 - Automobiles The rate of auto thefts triples every...Ch. 2.3 - Televisions The rate of television thefts is...Ch. 2.3 - Half-Life The half-life of cobalt 60 is 5 years....Ch. 2.3 - Half-Life The half-life of strontium 90 is 28...Ch. 2.3 - Prob. 55ECh. 2.3 - Prob. 56ECh. 2.3 - Aspirin Soon after taking an aspirin, a patient...Ch. 2.3 - Alcohol After a large number of drinks, a person...Ch. 2.3 - Prob. 59ECh. 2.3 - Prob. 60ECh. 2.3 - Prob. 61ECh. 2.3 - Prob. 62ECh. 2.3 - Prob. 63ECh. 2.3 - Prob. 64ECh. 2.3 - Richter Scale The Richter scale is used to measure...Ch. 2.3 - Sound Intensity The loudness of a sound is...Ch. 2.3 - Prob. 67ECh. 2.3 - Prob. 68ECh. 2.3 - On the same set of axes, graph y=lnx, y=Alnx, and...Ch. 2.3 - Prob. 70ECh. 2.3 - Prob. 71ECh. 2.3 - Of what use are logarithms, now that they are no...Ch. 2.3 - Prob. 73ECh. 2.3 - Prob. 74ECh. 2.3 - Prob. 75ECh. 2.3 - Prob. 76ECh. 2.3 - Prob. 77ECh. 2.4 - In Exercises 1-6, find N, A, and b; give a...Ch. 2.4 - Prob. 2ECh. 2.4 - Prob. 3ECh. 2.4 - Prob. 4ECh. 2.4 - Prob. 5ECh. 2.4 - Prob. 6ECh. 2.4 - Prob. 7ECh. 2.4 - Prob. 8ECh. 2.4 - Prob. 9ECh. 2.4 - Prob. 10ECh. 2.4 - Prob. 11ECh. 2.4 - Prob. 12ECh. 2.4 - Prob. 13ECh. 2.4 - Prob. 14ECh. 2.4 - Prob. 15ECh. 2.4 - Prob. 16ECh. 2.4 - Prob. 17ECh. 2.4 - In Exercises 17-20, use technology to find a...Ch. 2.4 - Prob. 19ECh. 2.4 - Prob. 20ECh. 2.4 - Prob. 21ECh. 2.4 - Prob. 22ECh. 2.4 - Prob. 23ECh. 2.4 - Prob. 24ECh. 2.4 - Internet Use The following graph shows the...Ch. 2.4 - Internet Use The following graph shows the...Ch. 2.4 - Prob. 27ECh. 2.4 - Epidemics Last year's epidemic of Martian flu...Ch. 2.4 - Sales You have sold 100 I Calculus T-shirts, and...Ch. 2.4 - Prob. 30ECh. 2.4 - Prob. 31ECh. 2.4 - Prob. 33ECh. 2.4 - College Basketball: Women The following table...Ch. 2.4 - Prob. 35ECh. 2.4 - Exercises 35 and 36 are based on the discussion...Ch. 2.4 - Prob. 37ECh. 2.4 - Prob. 38ECh. 2.4 - Prob. 39ECh. 2.4 - Prob. 40ECh. 2.4 - Prob. 41ECh. 2.4 - Prob. 42ECh. 2.4 - Prob. 43ECh. 2.4 - Prob. 44ECh. 2 - Sketch the graph of the quadratic functions in...Ch. 2 - Prob. 2RECh. 2 - Prob. 3RECh. 2 - Prob. 4RECh. 2 - Prob. 5RECh. 2 - Prob. 6RECh. 2 - Prob. 7RECh. 2 - Prob. 8RECh. 2 - Prob. 9RECh. 2 - Prob. 10RECh. 2 - Prob. 11RECh. 2 - Prob. 12RECh. 2 - Prob. 13RECh. 2 - Prob. 14RECh. 2 - In Exercises 15-18, find a formula of the form...Ch. 2 - Prob. 16RECh. 2 - Prob. 17RECh. 2 - Prob. 18RECh. 2 - Prob. 19RECh. 2 - Prob. 20RECh. 2 - In Exercises 21-24, use the given information to...Ch. 2 - In Exercises 21-24, use the given information to...Ch. 2 - Prob. 23RECh. 2 - Prob. 24RECh. 2 - Prob. 25RECh. 2 - In Exercises 25-28, find the time required, to the...Ch. 2 - In Exercises 25-28, find the time required, to the...Ch. 2 - In Exercises 25-28, find the time required, to the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - In Exercises 29-32, find an equation for the...Ch. 2 - Website Traffic The daily traffic (hits per day)...Ch. 2 - Revenue and Profit Some time ago, a consultant...Ch. 2 - Revenue and Profit Billy-Sean OHagan is John...Ch. 2 - Lobsters Marjory Duffin, CEO of Duffin House, is...Ch. 2 - Stock Prices In the period immediately following...Ch. 2 - Prob. 39RECh. 2 - Prob. 40RECh. 2 - Prob. 41RECh. 2 - Prob. 42RECh. 2 - Prob. 43RECh. 2 - Prob. 44RECh. 2 - Prob. 45RECh. 2 - Prob. 50RE
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- model a population p if its rate of growth is proportional to the amount present at time tarrow_forwardConsider an island that is separated from the mainland, which contains a pool of potential colonizer species. The MacArthur-Wilson theory of biogeography† hypothesizes that some species from the mainland will migrate to the island but that increasing competition on the island will lead to species extinction. It further hypothesizes that both the rate of migration and the rate of extinction of species are exponential functions, and that an equilibrium occurs when the rate of extinction matches the rate of immigration. This equilibrium point is thought to be the point at which immigration and extinction stabilize. Suppose that, for a certain island near the mainland, the rate of immigration of new species is given by the following formula. I = 5.0 ✕ 0.93t species per year Also suppose that the rate of species extinction on the island is given by the following formula. E = 1.7 ✕ 1.1t species per year According to the MacArthur-Wilson theory, how long will be required for stabilization…arrow_forwardgive an example of a function that is not a dirichlet function and justifyarrow_forward
- The logistic growth function describes the population, f(t), of an endangered species of elk t years after they were introduced to a nonthreatening habitat. a. How many elk were initially introduced to the habitat? b. How many elk are expected in the habitat after 10 years? c. What is the limiting size of the elk population that the habitat will sustain?arrow_forwardWho is the inventor of the logistic function? 1.Ludwig Ogistic 2.The iranian physicist Piver Verfraco 3.The Belgian mathematician Pierre François Verhulst.arrow_forwardIn the logistic model for population growth, dP/dt=P(8-2P), the carrying capacity of the population P(t) is:arrow_forward
- Suppose the probability π(x)π(x) of reaching a target (such as getting a ball between goal posts) as a function of distance x (in metres) from the target is well-fitted by a logistic regression equation withlog(π(x)/[1−π(x)])=6.1−0.13xPlease answer below to 3 significant digits.Part a)For this prediction model, what is the probability of reaching the target from a distance of 49 metres.Part b)At what distance is the probability of reaching the target equal to 0.6?arrow_forwardConsider an island separated from the mainland, which contains a pool of potential colonizer species. The MacArthur-Wilson theory of biogeography hypothesizes that some species from the mainland will migrate to the island but that increasing competition on the island will lead to species extinction. It further hypothesizes that both the rate of migration and the rate of extinction of species are exponential functions, and that an equilibrium occurs when the rate of extinction matches the rate of immigration. This equilibrium point is thought to be the point at which immigration and extinction stabilize. Suppose that, for a certain island near the mainland, the rate of immigration of new species is given by the following formula. I = 3.6 * 0.93t species per year Also suppose that the rate of species extinction on the island is given by the following formula. E = 1.4 * 1.1t species per year According to the MacArthur-Wilson theory, how long will be required for stabilization to occur and…arrow_forwardNitrogen dioxide, NO2, is an air pollutant resulting from burning fossil fuels in cars and power plants. The following table shows the decrease in the national average of the concentration in parts per billion (ppb) of NO2 for selected years. Year 2014 2015 2016 2017 2018 NO2 (ppb) 40.8107 39.7886 38.7972 37.8209 36.8752 Use exponential regression to find an exponential decay function for the concentration, C, of NO2 t years after 2014. Round constants to the nearest ten-thousandth. C = Use the model to predict the concentration of NO2 (in ppb) in 2050. Round to the nearest whole number. ? ppbarrow_forward
- Find the logistic function f with the given properties. f has limiting value 6 and passes through (0, 1) and (1, 2). HINT [First find A, then substitute.]arrow_forward71 A. No, it would not be appropriate because this data should be modeled by a quadratic function B. Yes, it would be appropriate because r2 is close to 1 C. Yes, it would be appropriate because employee growth should be modeled by a logistic function D. No, it would not be appropriate because t=14 is too far outside the range of known values, this would be extreme extrapolationarrow_forwardThe following table shows world population N, in billions, in the given year. According to the logistic model N = 10.90 / 1+2.23e^-0.030t, when will world population reach 90% of carrying capacity? Year N 1965 3.38 1970 3.72 1975 4.15 1980 4.48 1985 4.87 1990 5.38 1995 5.72 1999 6.05 a) 2064b) 2069c) 2066d) 2094arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning


Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning

Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
01 - What Is A Differential Equation in Calculus? Learn to Solve Ordinary Differential Equations.; Author: Math and Science;https://www.youtube.com/watch?v=K80YEHQpx9g;License: Standard YouTube License, CC-BY
Higher Order Differential Equation with constant coefficient (GATE) (Part 1) l GATE 2018; Author: GATE Lectures by Dishank;https://www.youtube.com/watch?v=ODxP7BbqAjA;License: Standard YouTube License, CC-BY
Solution of Differential Equations and Initial Value Problems; Author: Jefril Amboy;https://www.youtube.com/watch?v=Q68sk7XS-dc;License: Standard YouTube License, CC-BY