
Concept explainers
Solve the following problem over the interval from
(a) Analytically.
(b) Euler's method.
(c) Heun's method without iteration.
(d) Ralston's method.
(e) Fourth-order RK method.
(a)
To calculate: The solution of the initial value problem
Answer to Problem 2P
Solution: The solution to the initial value problem is
Explanation of Solution
Given Information:
The initial value problem
Formula used:
To solvean initial value problem of the form
Calculation:
Rewrite the provided differential equation as,
Integrate both sides to get,
Now use the initial condition
Hence, the analytical solution of the initial value problem is
(b)
To calculate: The solution of the initial value problem
Answer to Problem 2P
Solution: For
| t | y |
| 0 | 1 |
| 0.25 | 1.25 |
| 0.5 | 1.809017 |
| 0.75 | 2.817765 |
| 1 | 4.496385 |
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solvean initial value problem of the form
Calculation:
From the initial condition
Thus, evaluate the function
Further,
Proceed further and use the following MATLAB code to implement Euler’s method and solve the differential equation.
Execute the above code to obtain the solutions stored in matrix
The results thus obtained are tabulated as,
| T | y |
| 0 | 1 |
| 0.25 | 1.25 |
| 0.5 | 1.809017 |
| 0.75 | 2.817765 |
| 1 | 4.496385 |
(c)
To calculate: The solution of the initial value problem
Answer to Problem 2P
Solution: The solutions are tabulated as,
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
In the above expression,
Calculation:
From the initial condition
Thus, evaluate the function
And,
Thus,
Proceed further and use the following MATLAB code to implement Heun’s method and solve the differential equation.
Execute the above code to obtain the solutions stored in matrix
Theresults thus obtained aretabulated as,
(d)
To calculate: The solution of the initial value problem
Answer to Problem 2P
Solution: The solutions are tabulated as,
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
In the above expression,
Calculation:
From the initial condition
Thus, evaluate the function
And,
Thus,
Proceed further and use the following MATLAB code to implement Ralston’s method and solve the differential equation.
Execute the above code to obtain the solutions stored in matrix
The results thus obtained are tabulated as,
(e)
To calculate: The solution of the initial value problem
Answer to Problem 2P
Solution: The solutions are tabulated as,
Explanation of Solution
Given Information:
The initial value problem
Formula used:
Solve an initial value problem of the form
In the above expression,
Calculation:
From the initial condition
Ans,
And,
And,
Therefore,
Proceed further and use the following MATLAB code to implement RK method of order four, solve the differential equation, and compare the results obtained from part (a) to part (e) on a single plot.
Execute the above code to obtain the solutions stored in matrix
The results thus obtained are tabulated as,
Plot for all the methods along with the analytical solution
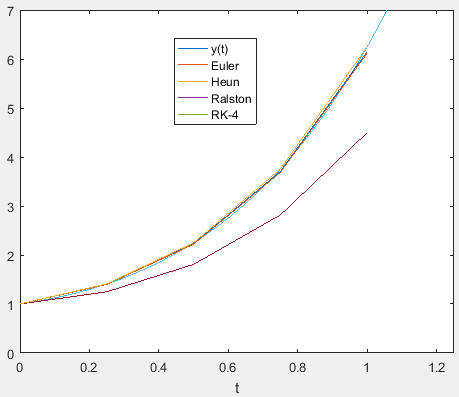
From the graph, it is inferred that the RK method of order 4 is the best approximation to the solution.
Want to see more full solutions like this?
Chapter 25 Solutions
Numerical Methods for Engineers
Additional Math Textbook Solutions
Fundamentals of Differential Equations (9th Edition)
Advanced Engineering Mathematics
Basic Technical Mathematics
A First Course in Probability
Algebra and Trigonometry: Structure and Method, Book 2
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






