Math
CalculusSingle Variable Calculus: Early Transcendentals, Volume I(a) A particle starts by moving to the right along a horizontal line; the graph of its position function is shown in the figure. When is the particle moving to the right? Moving to the left? Standing still? (b) Draw a graph of the veloc.ity function.
close solutoin list

(a) A particle starts by moving to the right along a horizontal line; the graph of its position function is shown in the figure. When is the particle moving to the right? Moving to the left? Standing still? (b) Draw a graph of the veloc.ity function.

BuyFind

Single Variable Calculus: Early Tr...

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781305270343
BuyFind

Single Variable Calculus: Early Tr...

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781305270343

Solutions

Chapter
Section
Problem 1E
Problem 2E
Problem 3E
Problem 4E
Problem 5E
Problem 6E
Problem 7E
Problem 8E
Problem 9E
Problem 10E
Problem 11E
Problem 12E
Problem 13E
Problem 14E
Problem 15E
Problem 16E
Problem 17E
Problem 18E
Problem 19E
Problem 20E
Problem 21E
Problem 22E
Problem 23E
Problem 24E
Problem 25E
Problem 26E
Problem 27E
Problem 28E
Problem 29E
Problem 30E
Problem 31E
Problem 32E
Problem 33E
Problem 34E
Problem 35E
Problem 36E
Problem 37E
Problem 38E
Problem 39E
Problem 40E
Problem 41E
Problem 42E
Problem 43E
Problem 44E
Problem 45E
Problem 46E
Problem 47E
Problem 48E
Problem 49E
Problem 50E
Problem 51E
Problem 53E
Problem 54E
Problem 55E
Problem 56E
Problem 57E
Problem 58E
Problem 59E
Problem 60E
Problem 61E
Chapter 2.7, Problem 11E
Textbook Problem

(a) A particle starts by moving to the right along a horizontal line; the graph of its position function is shown in the figure. When is the particle moving to the right? Moving to the left? Standing still?

(b) Draw a graph of the veloc.ity function.

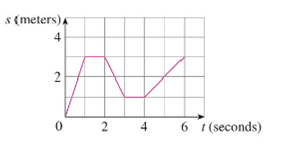
Chapter 2.7, Problem 11E, (a) A particle starts by moving to the right along a horizontal line; the graph of its position

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.See solution
Chapter 2.7,
Problem 10E
Chapter 2.7,
Problem 12E

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

See Solution

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 2 Solutions

Single Variable Calculus: Early Transcendentals, Volume I
Show all chapter solutions
Ch. 2.1 - A Lank holds 1000 gallons o f water, which drains...Ch. 2.1 - A cardiac monitor is used to measure the heart...Ch. 2.1 - The point P(2, 1) lies on the curve y = 1/(1 x)....Ch. 2.1 - The point P(0.5, 0) lies on the curve y = cos x....Ch. 2.1 - If a ball is thrown into the air with a velocity...Ch. 2.1 - If a rock is thrown upward on the planet Mars with...Ch. 2.1 - The table shows the position of a motorcyclist...Ch. 2.1 - The displacement (in centimeters) of a particle...Ch. 2.1 - The point P(1, 0) lies on the curve y = sin(l0/x)....Ch. 2.2 - Explain in your own words what is meant by the...
Ch. 2.2 - Explain what it means to say that...Ch. 2.2 - Explain the meaning of each of the following. (a)...Ch. 2.2 - Use the given graph of f to state the value of...Ch. 2.2 - For the function f whose graph is given, state the...Ch. 2.2 - For the function h whose graph is given, state the...Ch. 2.2 - For the function g whose graph is given, state the...Ch. 2.2 - For the function A whose graph is shown, state the...Ch. 2.2 - For the function f whose graph is shown, state the...Ch. 2.2 - A patient receives a 150-mg injection of a drug...Ch. 2.2 - Sketch the graph of the function and use it to...Ch. 2.2 - Sketch the graph of the function and use it to...Ch. 2.2 - Use the graph of the function f to state the value...Ch. 2.2 - Use the graph of the function f to state the value...Ch. 2.2 - Sketch the graph of an example of a function f...Ch. 2.2 - Sketch the graph of an example of a function f...Ch. 2.2 - Sketch the graph of an example of a function f...Ch. 2.2 - Sketch the graph of an example of a function f...Ch. 2.2 - Guess the value of the limit (if it exists) by...Ch. 2.2 - Guess the value of the limit (if it exists) by...Ch. 2.2 - Guess the value of the limit (if it exists) by...Ch. 2.2 - Guess the value of the limit (if it exists) by...Ch. 2.2 - Use a table of Values to estimate i:he value of...Ch. 2.2 - Use a table of Values to estimate i:he value of...Ch. 2.2 - Use a table of Values to estimate i:he value of...Ch. 2.2 - Use a table of Values to estimate i:he value of...Ch. 2.2 - Use a table of Values to estimate i:he value of...Ch. 2.2 - Use a table of Values to estimate i:he value of...Ch. 2.2 - (a) By graphing the function f(x) = (cos 2x cos...Ch. 2.2 - (a) Estimate the value of limx0sinxsinx by...Ch. 2.2 - Determine the infinite limit. limx5+x+1x5Ch. 2.2 - Determine the infinite limit. limx5x+1x5Ch. 2.2 - Determine the infinite limit. limx12x(x1)2Ch. 2.2 - Determine the infinite limit. limx3x(x3)5Ch. 2.2 - Determine the infinite limit. limx3+ln(x29)Ch. 2.2 - Determine the infinite limit. limx0+ln(sinx)Ch. 2.2 - Determine the infinite limit. limx(/2)+1xsecxCh. 2.2 - Determine the infinite limit. limxcotxCh. 2.2 - Determine the infinite limit. limx2xcscxCh. 2.2 - Determine the infinite limit. limx2x22xx24x+4Ch. 2.2 - Determine the infinite limit. limx2+x22x8x25x+6Ch. 2.2 - Determine the infinite limit. limx0+(1xlnx)Ch. 2.2 - Determine the infinite limit. limx0(lnx2x2)Ch. 2.2 - (a) Find the vertical asymptotes of the function...Ch. 2.2 - Determine limx11x31 and limx1+1x31 (a) by...Ch. 2.2 - (a) By graphing the function f(x) = (tan 4x)/x and...Ch. 2.2 - (a) Estimate the value of the limit limx0 (1 +...Ch. 2.2 - (a) Evaluate the function f(x) = x2 (2x/1000) for...Ch. 2.2 - (a) Evaluate h(x) = (tan x x)/x3 for x = 1, 0.5,...Ch. 2.2 - Graph the function f(x) = sin(/x) of Example 4 in...Ch. 2.2 - Consider the function f(x) = tan1x. (a) Show that...Ch. 2.2 - Use a graph to estimate the equations of all the...Ch. 2.2 - In the theory of relativity, the mass of a...Ch. 2.2 - (a) Use numerical and graphical evidence to guess...Ch. 2.3 - Given that limx2f(x)=4limx2g(x)=2limx2h(x)=0 find...Ch. 2.3 - Tire graphs of f and g are given. Use them to...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - Evaluate the limit and justify each step by...Ch. 2.3 - (a) What is wrong with the following equation?...Ch. 2.3 - Evaluate the limit, if it exists. limx2x2+x5x5Ch. 2.3 - Evaluate the limit, if it exists. limx3x2+3xx2x12Ch. 2.3 - Evaluate the limit, if it exists. limx5x25x+6x5Ch. 2.3 - Evaluate the limit, if it exists. limx4x2+3xx2x12Ch. 2.3 - Evaluate the limit, if it exists. limt3t292t2+7t+3Ch. 2.3 - Evaluate the limit, if it exists....Ch. 2.3 - Evaluate the limit, if it exists. limh0(5+h)225hCh. 2.3 - Evaluate the limit, if it exists. limh0(2+h)38hCh. 2.3 - Evaluate the limit, if it exists. limx2x+2x3+8Ch. 2.3 - Evaluate the limit, if it exists. limt1t41t31Ch. 2.3 - Evaluate the limit, if it exists. limh09+h3hCh. 2.3 - Evaluate the limit, if it exists. limu24u+13u2Ch. 2.3 - Evaluate the limit, if it exists. limx31x13x3Ch. 2.3 - Evaluate the limit, if it exists. limh0(3+h)131hCh. 2.3 - Evaluate the limit, if it exists. limt01+t1ttCh. 2.3 - Evaluate the limit, if it exists. limt0(1t1t2+t)Ch. 2.3 - Evaluate the limit, if it exists. limx164x16xx2Ch. 2.3 - Evaluate the limit, if it exists....Ch. 2.3 - Evaluate the limit, if it exists. limt0(1t1+t1t)Ch. 2.3 - Evaluate the limit, if it exists. limx4x2+95x+4Ch. 2.3 - Evaluate the limit, if it exists. limh0(x+h)x3hCh. 2.3 - Evaluate the limit, if it exists. limh01(xh)21x2hCh. 2.3 - (a) Estimate the value of limx0x1+3x1 by graphing...Ch. 2.3 - (a) Use a graph of f(x)=3+x3x to estimate the...Ch. 2.3 - Use the Squeeze Theorem to show that...Ch. 2.3 - Use the Squeeze Theorem to show that...Ch. 2.3 - If 4x 9 f(x) x2 4x + 7 for x 0, find limx4f(x)Ch. 2.3 - If 2x g(x) x4 x2 + 2 for all x, evaluate...Ch. 2.3 - Prove that limx0x4cos2x=0.Ch. 2.3 - Prove that limxxesin(/x)=0.Ch. 2.3 - Find the limit, if it exists. If the limit does...Ch. 2.3 - Find the limit, if it exists. If the limit does...Ch. 2.3 - Find the limit, if it exists. If the limit does...Ch. 2.3 - Find the limit, if it exists. If the limit does...Ch. 2.3 - Find the limit, if it exists. If the limit does...Ch. 2.3 - Find the limit, if it exists. If the limit does...Ch. 2.3 - The signum (or sign)function, denoted by sgn, is...Ch. 2.3 - Let g(x) =sgn(sinx). (a) Find each of the...Ch. 2.3 - Let g(x)=x2+x6x2 (a) Find (i) limx2+g(x) (ii)...Ch. 2.3 - Let f(x)={x2+1ifx1(x2)2ifx1 (a) Find limx0...Ch. 2.3 - Let B(t)={412tift2t+cift2 Find the value of c so...Ch. 2.3 - l.et g(x)={xifx13ifx=12xif1x2x3ifx2 (a) Evaluate...Ch. 2.3 - (a) If the symbol denotes the greatest integer...Ch. 2.3 - Let f(x)=cosx,x. (a) Sketch the graph of f. (b)...Ch. 2.3 - If f(x)=x+x, show that lim x0 f(x) exists hut is...Ch. 2.3 - In the theory of relativity, the Lorentz...Ch. 2.3 - If p is a polynomial, Show that limxa p(x) = p(a)Ch. 2.3 - If r is a rational function. use Exercise 57 to...Ch. 2.3 - If limx1f(x)8x1=10, find limx1f(x).Ch. 2.3 - If limx0f(x)x2=5, find the following limits. (a)...Ch. 2.3 - If f(x)={x2ifxisrational0ifxisirrational prove...Ch. 2.3 - Show by means of an example that limxa[f(x)+g(x)]...Ch. 2.3 - Show by means of an example that limxa[f(x)g(x)]...Ch. 2.3 - Evaluate limx26x23x1.Ch. 2.3 - Is there a number a such that limx23x2+ax+a+3x2+x2...Ch. 2.3 - The figure shows a fixed circle C1, with equation...Ch. 2.4 - Use the given graph of f to find a number such...Ch. 2.4 - Use the given graph of f to find a number such...Ch. 2.4 - Use the given graph of f(x)=x to find a number ...Ch. 2.4 - Use the given graph of f(x) =x2 to find a number ...Ch. 2.4 - Use a graph to find a number such that if...Ch. 2.4 - Use a graph to find a number such that if...Ch. 2.4 - For the limit limx2(x33x+4)=6 illustrate...Ch. 2.4 - For the limit limx0e2x1x=2 illustrate Definition 2...Ch. 2.4 - (a) Use a graph to find a number such that if 2 x...Ch. 2.4 - Given that limxcsc2=, illustrate Definition 6 by...Ch. 2.4 - A machinist is required to manufacture a circular...Ch. 2.4 - A crystal growth furnace is used in research to...Ch. 2.4 - (a) Find a number such that if |x 2| , then |4x ...Ch. 2.4 - Given that limx2(5x7)=3, illustrate Definition 2...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Prove the statement using the , definition of a...Ch. 2.4 - Verify that another possible choice of for...Ch. 2.4 - Verify, by a geometric argument, that the largest...Ch. 2.4 - Prove that limx21x=12.Ch. 2.4 - Prove that limxax=aifa0. [Hint:Usexa=xax+a]Ch. 2.4 - If H is the Heaviside function defined in Example...Ch. 2.4 - If the function f is defined by...Ch. 2.4 - By comparing Definitions 2, 3, and 4, prove...Ch. 2.4 - How close to 3 do we have to take x so that...Ch. 2.4 - Prove, using Definition 6, that limx31(x+3)4=...Ch. 2.4 - Prove that limx0+lnx=Ch. 2.4 - Suppose that limxaf(x)=andlimxag(x)=c, where c is...Ch. 2.5 - Write an equation that expresses the fact that a...Ch. 2.5 - If f is continuous on ( , ).what can you say about...Ch. 2.5 - (a) From the graph of f , state the numbers at...Ch. 2.5 - From the graph of g, state the intervals on which...Ch. 2.5 - Sketch the graph of a function f that is...Ch. 2.5 - Sketch the graph of a function f that is...Ch. 2.5 - Sketch the graph of a function f that is...Ch. 2.5 - Sketch the graph of a function f that is...Ch. 2.5 - The toll T charged for driving on a certain...Ch. 2.5 - Explain why each function is continuous or...Ch. 2.5 - Use the definition of continuity and the...Ch. 2.5 - Use the definition of continuity and the...Ch. 2.5 - Use the definition of continuity and the...Ch. 2.5 - Use the definition of continuity and the...Ch. 2.5 - Use the definition of continuity and the...Ch. 2.5 - Use the definition of continuity and the...Ch. 2.5 - Explain why the function is discontinuous at the...Ch. 2.5 - Explain why the function is discontinuous at the...Ch. 2.5 - Explain why the function is discontinuous at the...Ch. 2.5 - Explain why the function is discontinuous at the...Ch. 2.5 - Explain why the function is discontinuous at the...Ch. 2.5 - Explain why the function is discontinuous at the...Ch. 2.5 - How would you "remove the discontinuity" of f? In...Ch. 2.5 - How would you "remove the discontinuity" of f? In...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Explain, using Theorems 4, 5, 7, and 9, why the...Ch. 2.5 - Locate the discontinuities of the function and...Ch. 2.5 - Locate the discontinuities of the function and...Ch. 2.5 - Use continuity to evaluate the limit. limx2x20x2Ch. 2.5 - Use continuity to evaluate the limit....Ch. 2.5 - Use continuity to evaluate the limit....Ch. 2.5 - Use continuity to evaluate the limit. limx43x22x4Ch. 2.5 - Show that f is continuous on ( , )....Ch. 2.5 - Show that f is continuous on ( , )....Ch. 2.5 - Find the numbers at which f is discontinuous. At...Ch. 2.5 - Find the numbers at which f is discontinuous. At...Ch. 2.5 - Find the numbers at which f is discontinuous. At...Ch. 2.5 - The gravitational force exerted by the planet...Ch. 2.5 - For what value of the constant c is the function f...Ch. 2.5 - Find the values of a and h that make f continuous...Ch. 2.5 - Suppose f and g are continuous functions such that...Ch. 2.5 - Let f(x)=1/xandg(x)=1/x2. (a) Find (f g)(x). (b)...Ch. 2.5 - Which of the following functions .f has a...Ch. 2.5 - Suppose that a function f is continuous on [0, 1]...Ch. 2.5 - If f(x) = x2 + 10 sin x, show that there is a...Ch. 2.5 - Suppose f is continuous on [1, 5] and the only...Ch. 2.5 - Use the Intermediate Value Theorem to show that...Ch. 2.5 - Use the Intermediate Value Theorem to show that...Ch. 2.5 - Use the Intermediate Value Theorem to show that...Ch. 2.5 - Use the Intermediate Value Theorem to show that...Ch. 2.5 - (a) Prove that the equation has at least one real...Ch. 2.5 - (a) Prove that the equation has at least one real...Ch. 2.5 - (a) Prove that the equation has at least one real...Ch. 2.5 - (a) Prove that the equation has at least one real...Ch. 2.5 - Prove, without graphing, that the graph of the...Ch. 2.5 - Prove, without graphing, that the graph of the...Ch. 2.5 - Prove that f is continuous at a if and only if...Ch. 2.5 - To prove that sine is continuous, we need to show...Ch. 2.5 - Prove that cosine is a continuous function.Ch. 2.5 - (a) Prove Theorem 4, part 3. (b) Prove Theorem 4,...Ch. 2.5 - For what values of x is f continuous?...Ch. 2.5 - For what values of x is g continuous?...Ch. 2.5 - Is there a number that is exactly 1 more than its...Ch. 2.5 - If a and b are positive numbers, prove that the...Ch. 2.5 - Show that the function f(x)={x4sin(1/x)ifx00ifx=0...Ch. 2.5 - (a) Show that the absolute value function F(x) = |...Ch. 2.6 - Explain in your own words tile meaning of each of...Ch. 2.6 - (a) Can the graph of y = f(x) intersect a vertical...Ch. 2.6 - For the function f whose graph is given, state the...Ch. 2.6 - For the function g whose graph is given, state the...Ch. 2.6 - Sketch the graph of an example of a function f...Ch. 2.6 - Sketch the graph of an example of a function f...Ch. 2.6 - Sketch the graph of an example of a function f...Ch. 2.6 - Sketch the graph of an example of a function f...Ch. 2.6 - Sketch the graph of an example of a function f...Ch. 2.6 - Sketch the graph of an example of a function f...Ch. 2.6 - Guess the value of the limit limxx22x by...Ch. 2.6 - (a) Use a graph of f(x)=(12x)x to estimate the...Ch. 2.6 - Evaluate the limit and justify each step by...Ch. 2.6 - Evaluate the limit and justify each step by...Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - Find the limit or show that it does not exist....Ch. 2.6 - (a) For F(x)=xlnx find each of the following...Ch. 2.6 - For f(x)=2x1lnx find each of the following limits....Ch. 2.6 - (a) Estimate the value of limx(x2+x+1+x) by...Ch. 2.6 - (a) Use a graph of f(x)=3x2+8x+63x2+3x+1 to...Ch. 2.6 - Find the horizontal and vertical asymptotes of...Ch. 2.6 - Find the horizontal and vertical asymptotes of...Ch. 2.6 - Find the horizontal and vertical asymptotes of...Ch. 2.6 - Find the horizontal and vertical asymptotes of...Ch. 2.6 - Find the horizontal and vertical asymptotes of...Ch. 2.6 - Find the horizontal and vertical asymptotes of...Ch. 2.6 - Estimate the horizontal asymptote of the function...Ch. 2.6 - (a) Graph the function f(x)=2x2+13x5 How many...Ch. 2.6 - Let P and Q be polynomials. Find limxP(x)Q(x) if...Ch. 2.6 - Make a rough sketch of the curve y = xn (n an...Ch. 2.6 - Find a formula for a function f that satisfies the...Ch. 2.6 - Find a formula for a function that has vertical...Ch. 2.6 - A function f is a ratio of quadratic functions and...Ch. 2.6 - Find the limits as x and as x . Use this...Ch. 2.6 - Find the limits as x and as x . Use this...Ch. 2.6 - Find the limits as x and as x . Use this...Ch. 2.6 - Find the limits as x and as x . Use this...Ch. 2.6 - Find the limits as x and as x . Use this...Ch. 2.6 - (a) Use the Squeeze Theorem to evaluate limxsinxx....Ch. 2.6 - By the end behavior of a function we mean the...Ch. 2.6 - Find limxf(x) if, for all x 1, 10ex212exf(x)5xx1Ch. 2.6 - (a) A tank contains 5000 L of pure water. Brine...Ch. 2.6 - In Chapter 9 we will be able to show, under...Ch. 2.6 - (a) By graphing y = ex/10 and y = 0.1 on a common...Ch. 2.6 - Use a graph to find a number N such that if x N...Ch. 2.6 - For the limit limx13xx2+1=3 illustrate Definition...Ch. 2.6 - For the limit limx13xx2+1=3 illustrate Definition...Ch. 2.6 - For the limit limxxlnx= illustrate Definition 9 by...Ch. 2.6 - (a) How large do we have to take x so that 1/x2 ...Ch. 2.6 - (a) How large do we have to take x so that...Ch. 2.6 - Use Definition 8 to prove that limx1x=0....Ch. 2.6 - Prove, using Definition 9, that limxx3=....Ch. 2.6 - Use Definition 9 to prove that limxex=. Definition...Ch. 2.6 - Formulate a precise definition of limxf(x)= Then...Ch. 2.6 - (a) Prove that limxf(x)=limt0+f(1/t) and...Ch. 2.7 - A curve has equation y = f(x) (a) Write an...Ch. 2.7 - Graph the curve y = ex in the viewing rectangles [...Ch. 2.7 - (a) Find the slope of the tangent line to the...Ch. 2.7 - (a) Find the slope of the tangent line to the...Ch. 2.7 - Find an equation of the tangent line to the curve...Ch. 2.7 - Find an equation of the tangent line to the curve...Ch. 2.7 - Find an equation of the tangent line to the curve...Ch. 2.7 - Find an equation of the tangent line to the curve...Ch. 2.7 - (a) Find the slope of the tangent to the curve y =...Ch. 2.7 - (a) Find the slope of the tangent to the curve...Ch. 2.7 - (a) A particle starts by moving to the right along...Ch. 2.7 - Shown are graphs of the position functions of two...Ch. 2.7 - If a ball is thrown into the air with a velocity...Ch. 2.7 - If a rock is thrown upward on the planet Mars with...Ch. 2.7 - The displacement (in meters) of a particle moving...Ch. 2.7 - The displacement (in feel) of a particle moving in...Ch. 2.7 - For the function g whose graph is given, arrange...Ch. 2.7 - The graph of a function f is shown. (a) Find the...Ch. 2.7 - For the function f graphed in Exercise 18: (a)...Ch. 2.7 - Find an equation of the tangent line to the graph...Ch. 2.7 - If an equation of the tangent tine to the curve y...Ch. 2.7 - If the tangent line to y= f(x) at (4, 3) passes...Ch. 2.7 - Sketch the graph of a function f for which f(0) =...Ch. 2.7 - Sketch the graph of a function g for which g(0) =...Ch. 2.7 - Sketch the graph of a function q that is...Ch. 2.7 - Sketch the graph of a function f where the domain...Ch. 2.7 - If f(x) = 3x2 x3 , find f'(l) and use it to find...Ch. 2.7 - If g(x) = x4 2, find g'(l) and use it to find an...Ch. 2.7 - (a) If F(x) = 5x/(l + x2), find F'(2) and use it...Ch. 2.7 - (a) If G(x) = 4x2 x3, find G'(a) and use it to...Ch. 2.7 - Find f'(a). f(x) = 3x2 4x + 1Ch. 2.7 - Find f'(a). f(t) = 2t3 + tCh. 2.7 - Find f'(a). f(t)=2t+1t+3Ch. 2.7 - Find f'(a). f(x) = x2Ch. 2.7 - Find f'(a). f(x)=12xCh. 2.7 - Find f'(a). f(x)=41xCh. 2.7 - Each limit represents the derivative of some...Ch. 2.7 - Each limit represents the derivative of some...Ch. 2.7 - Each limit represents the derivative of some...Ch. 2.7 - Each limit represents the derivative of some...Ch. 2.7 - Each limit represents the derivative of some...Ch. 2.7 - Each limit represents the derivative of some...Ch. 2.7 - A particle moves along a straight line with...Ch. 2.7 - A particle moves along a straight line with...Ch. 2.7 - A warm can of soda is placed in a cold...Ch. 2.7 - A roast is taken from an over when its temperature...Ch. 2.7 - Reasearchers measured the average blood alcohol...Ch. 2.7 - The number N of locations of a popular coffeehouse...Ch. 2.7 - The table shows world average daily oil...Ch. 2.7 - The table shows values of the viral load V(r) in...Ch. 2.7 - The cost (in dollars) of producing x units of a...Ch. 2.7 - The cost of producing x ounces of gold from a new...Ch. 2.7 - The number of bacteria after r hours in a...Ch. 2.7 - Let H(t) be the daily cost (in dollars) to heat an...Ch. 2.7 - The quantity (in pounds) of a gourmet ground...Ch. 2.7 - The quantity of oxygen that can dissolve in water...Ch. 2.7 - The graph shows the influence of the temperature T...Ch. 2.7 - Determine whether f'(0) exists....Ch. 2.7 - Determine whether f'(0) exists....Ch. 2.7 - (a) Graph the function f(x)=sinx11000sin(1000x) in...Ch. 2.8 - Use the given graph to estimate the value of each...Ch. 2.8 - Use the given graph to estimate the value of each...Ch. 2.8 - Match the graph of each function in (a)(d) with...Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Trace or copy the graph of the given function .f....Ch. 2.8 - Shown is the graph of the population function P(t)...Ch. 2.8 - A rechargeable battery is plugged into a charger....Ch. 2.8 - The graph (from the US Department of Energy) shows...Ch. 2.8 - The graph shows how the average age of first...Ch. 2.8 - Make a careful sketch of the graph if .f and below...Ch. 2.8 - Make a careful sketch of the graph if .f and below...Ch. 2.8 - Make a careful sketch of the graph if .f and below...Ch. 2.8 - Let .f (x) = x2. (a) Estimate the values of f'(0),...Ch. 2.8 - Let f(x) = x3. (a) Estimate the values of f'(0),...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - Find the derivative of the function using the...Ch. 2.8 - (a) Sketch the graph of f(x)=6x by starting with...Ch. 2.8 - (a) If f(x) = x4 + 2x, find f'(x). (b) Check to...Ch. 2.8 - (a) If f(x) = x + 1/x, find f'(x). (b) Chock to...Ch. 2.8 - The unemployment rate U(t) varies with time. The...Ch. 2.8 - The table gives the number N(t), measured in...Ch. 2.8 - The table gives the height as time passes of a...Ch. 2.8 - Water temperature affects the growth rate of brook...Ch. 2.8 - Let P represent the percentage of a city's...Ch. 2.8 - Suppose N is the number of people in the United...Ch. 2.8 - The graph of f is given. State, with reasons, the...Ch. 2.8 - The graph of f is given. State, with reasons, the...Ch. 2.8 - The graph of f is given. State, with reasons, the...Ch. 2.8 - The graph of f is given. State, with reasons, the...Ch. 2.8 - Graph the function f(x)=x+x. Zoom in repeatedly,...Ch. 2.8 - Zoom in toward the points (1, 0), (0, 1). and (1,...Ch. 2.8 - The graphs of a function f and its derivative f'...Ch. 2.8 - The graphs of a function f and its derivative f'...Ch. 2.8 - The figure shows the graphs of f, f', and f"....Ch. 2.8 - The figure shows graphs of f; f', f", and f'"....Ch. 2.8 - The figure shows the graphs of three functions....Ch. 2.8 - The figure shows the graphs of four functions. One...Ch. 2.8 - Use the definition of a derivative to find f'(x)...Ch. 2.8 - Use the definition of a derivative to find f'(x)...Ch. 2.8 - If f(x) = 2x2 x3, find f'(x), f"(x), f'"(x), and...Ch. 2.8 - (a) The graph of a position function of a car is...Ch. 2.8 - Let f(x)=x3. (a) If a 0, use Equation 2 .7 .5 to...Ch. 2.8 - (a) If g(x) = x2/3, show that g'(0) does not...Ch. 2.8 - Show that the function f(x) = | x 6| is not...Ch. 2.8 - Where is the greatest integer function f(x) = [[ x...Ch. 2.8 - (a) Sketch the graph of the function f(x) = x |x...Ch. 2.8 - (a) Sketch the graph of the function g(x) = x +...Ch. 2.8 - Recall that a function f is called even if f(x) =...Ch. 2.8 - The left-hand and right-hand derivatives off at a...Ch. 2.8 - Nick starts jogging and runs faster and faster for...Ch. 2.8 - When you turn on a hot -water faucet, the...Ch. 2.8 - Let f be the tangent line to the parabola y = x2...Ch. 2 - Explain what each of the following means and...Ch. 2 - Describe several ways in which a limit can fail to...Ch. 2 - State the following limit Laws. (a) Sum Law (b)...Ch. 2 - What does the Squeeze Theorem say?Ch. 2 - (a) What does it mean to say that the line x = a...Ch. 2 - Which of the following curves have vertical...Ch. 2 - (a) What does it mean for f to be continuous at a?...Ch. 2 - (a) Give examples of functions that a:e continuous...Ch. 2 - What does the Intermediate Value Theorem say?Ch. 2 - Write an expression for the slope of the tangent...Ch. 2 - Suppose an object moves along a straight line...Ch. 2 - If y = f(x) and x changes from x1, to x2, write...Ch. 2 - Define the derivative f'(a). Discuss two way of...Ch. 2 - Define the second derivative of f. If f(t) is the...Ch. 2 - (a) What does it mean for f to be differentiable...Ch. 2 - Describe several ways in which a function can fail...Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - Determine whether the statement is true or false....Ch. 2 - The graph of f is given. (a) Find each limit, or...Ch. 2 - Sketch the graph of a function f that satisfies...Ch. 2 - Find the limit. limx1ex3xCh. 2 - Find the limit. limx3x29x2+2x3Ch. 2 - Find the limit. limx3x29x2+2x3Ch. 2 - Find the limit. limx1+x29x2+2x3Ch. 2 - Find the limit. limh0(h1)3+1hCh. 2 - Find the limit. limt2t24t38Ch. 2 - Find the limit. limr9r(r9)4Ch. 2 - Find the limit. limv4+4v4vCh. 2 - Find the limit. limu1u41u3+5u26uCh. 2 - Find the limit. limx3x+6xx33x2Ch. 2 - Find the limit. limxx292x6Ch. 2 - Find the limit. limxx292x6Ch. 2 - Find the limit. limxln(sinx)Ch. 2 - Find the limit. limx12x2x45+x3x4Ch. 2 - Find the limit. limx(x2+4x+1x)Ch. 2 - Find the limit. limxexx2Ch. 2 - Find the limit. limx0+tan1(1/x)Ch. 2 - Find the limit. limx1(1x1+1x23x+2)Ch. 2 - Use graphs to discover the asymptotes of the...Ch. 2 - Use graphs to discover the asymptotes of the...Ch. 2 - If 2x 1 f(x) x2 for 0 x 3, find limx1f(x).Ch. 2 - Prove that limx0x2cos(1/x2)=0.Ch. 2 - Prove the statement using the precise definition...Ch. 2 - Prove the statement using the precise definition...Ch. 2 - Prove the statement using the precise definition...Ch. 2 - Prove the statement using the precise definition...Ch. 2 - Let f(x)={xifx03xif0x3(x3)2ifx3 (a) Evaluate each...Ch. 2 - Let g(x)={2xx2if0x22xif2x3x4if3x4ifx4 a) For each...Ch. 2 - Show that the function is continuous on its...Ch. 2 - Show that the function is continuous on its...Ch. 2 - Use the Intermediate Value Theorem to show that...Ch. 2 - Use the Intermediate Value Theorem to show that...Ch. 2 - (a) Find the slope of the tangent line to the...Ch. 2 - Find equations of the tangent lines to the curve...Ch. 2 - The displacement (in meters) of an object moving...Ch. 2 - According to Boyle's Law, if the temperature of a...Ch. 2 - (a) Use the definition of a derivative to find...Ch. 2 - Find a function f and a number a such that...Ch. 2 - The total cost of repaying a student loan at an...Ch. 2 - Trace or copy the graph of the function. Then...Ch. 2 - Trace or copy the graph of the function. Then...Ch. 2 - Trace or copy the graph of the function. Then...Ch. 2 - (a) If f(x)=35x, use the definition of a...Ch. 2 - (a) Find the asymptotes of the graph of f(x)=4x3+x...Ch. 2 - The graph of .f is shown. State, with reasons, the...Ch. 2 - The figure shows the graphs of f, f', and f"....Ch. 2 - Sketch the graph or a function .f that satisfies...Ch. 2 - Let P(t) be the percentage of Americans under the...Ch. 2 - Let B(t) be the number of US 20 bills in...Ch. 2 - The total fertility rate at time t, denoted by...Ch. 2 - Suppose that | f(x) | g(x) for all x, where...Ch. 2 - Let f(x)=x+x. (a) For what values of a does...Ch. 2 - Evaluate limx1x31x1Ch. 2 - Find numbers a and b such that limx0ax+b2x=1.Ch. 2 - Evaluate limx02x12x+1x.Ch. 2 - The figure shows a point P on the parabola y = x2...Ch. 2 - Evaluate the following limits, if they exist,...Ch. 2 - Sketch the region in the plane defined by each of...Ch. 2 - Find all values of a such that f is continuo us on...Ch. 2 - A fixed point of a function f is a number c in its...Ch. 2 - If limxa[f(x)+g(x)]=2andlimxa[f(x)g(x)]=1, find...Ch. 2 - (a) The figure shows an isosceles triangle ABC...Ch. 2 - (a) If we start. from 0 latitude and proceed in a...Ch. 2 - If f is a differentiable function and g(x) =...Ch. 2 - Suppose f is a function that satisfies the...Ch. 2 - Suppose f is a function with the property that |...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Show solutions
Sketch several level curves of the function. 5. f(x,y)=4x2+y2

Multivariable Calculus

Evaluate the expression sin Exercises 116. (23)2

Finite Mathematics and Applied Calculus (MindTap Course List)

Inequalities Solve the inequality. Express the solution using interval notation and graph the solution set on t...

Precalculus: Mathematics for Calculus (Standalone Book)

Finding Derivatives In Exercises 2940, find the derivative of the function. y=6

Calculus: An Applied Approach (MindTap Course List)

By any method, determine all possible real solutions of each equation in Exercises 1330. Check your answers by ...

Applied Calculus

Simplify the expression. 70. tan(sin1 x)

Calculus: Early Transcendentals

Sketching the Graph of a Logarithmic Function In Exercises 61-68, sketch the graph of the function and state It...

Calculus: Early Transcendental Functions

Identify the circumstances in which the median may be better than the mean as a measure of central tendency and...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

A random sample of 100 patients treated in a program for alcoholism and drug dependency over the past 10 years ...

Essentials Of Statistics

Let P(x1,y1) be a point on the ellipse x2/a2+y2/b2=1 with foci F1 and F2 and let and be the angles between th...

Calculus (MindTap Course List)

A random sample is obtained from a normal population with a mean of =95 and a standard deviation of =40 . The s...

Statistics for The Behavioral Sciences (MindTap Course List)

In Exercises 19 and 20, determine whether the lines AB and CD are parallel. 20. A(2, 3), B(2, 2) and C(2, 4), D...

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

Prove the statement using the precise definition of a limit. 44. limx4+2x4=

Single Variable Calculus

A chemical supply company currently has in stock 100 lb of a certain chemical, which it sells to customers in 5...

Probability and Statistics for Engineering and the Sciences

In Exercises 516, evaluate the given quantity. log4164

Finite Mathematics

Critical Thinking If a data set has an even number of data, is it true or false that the median is never equal ...

Understanding Basic Statistics

For Problems 1-10, answer true or false. The value, in dollars, of x five-dollar bills and y ten-dollar bills c...

Intermediate Algebra

For exercises 36 and 37, EFis the median of trapezoid ABCD in the figure above. Suppose that AB=12.8andDC=18.4 ...

Elementary Geometry For College Students, 7e

Counting Problem In how many different ways can a basketball team win exactly four out of their last six games?

Mathematical Excursions (MindTap Course List)

Solve each equation: 10x2+29x+10=0

Elementary Technical Mathematics

34. If find the following. (b) (c) (d)

Mathematical Applications for the Management, Life, and Social Sciences

Use the pie chart "Century Mutual Fund - Investments" for Exercises 45 and 46. 47. Ford Motor Co. announced tha...

Contemporary Mathematics for Business & Consumers

Differential Equation In Exercises 51-56, find the general solution of the differential equation. dydx=(ex+5)2

Calculus: Early Transcendental Functions (MindTap Course List)

Finding a Taylor Series In Exercises 5-16, use the definition of Taylor series to find the Taylor series, cente...

Calculus of a Single Variable

Find all solutions of the equation. 21. x2 + 2x + 5 = 0

Single Variable Calculus: Early Transcendentals

Use the unit circle and the fact that cosine is an even function to find each of the following: cos(135)

Trigonometry (MindTap Course List)

The minimum distance of a code is defined to be the smallest distance between any pair of distinct code words i...

Elements Of Modern Algebra

For a = 6i − j and b = 2i + 3j, a + 2b = 2i − 4j 8i − 2j 16i − 4j 10i + 5j

Study Guide for Stewart's Multivariable Calculus, 8th

Sometimes, Always, or Never: If limxaf(x) and f(a) both exist, then f is continuous at a.

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

Let Z be the standard normal variable. Find the values of z if z satisfies: a. P(Zz)=.9713b. P(zZ)=.9713.

Finite Mathematics for the Managerial, Life, and Social Sciences

Given: BD bisects ABC mABD=2x+15 mDBC=3x+5 Find: mABC

Elementary Geometry for College Students

Finding the Interval of Convergence In Exercises 1538, find the Interval of convergence of the power series. (B...

Calculus (MindTap Course List)

Finding an Indefinite Integral In Exercises 25-32, use substitution and partial fractions to find the indefinit...

Calculus

Finding Velocity and Acceleration Vectors in Space In Exercises 37-40, the position vector r describes the path...

Multivariable Calculus

Describe the characteristics of a within-subjects experimental research design.

Research Methods for the Behavioral Sciences (MindTap Course List)

Write each expression without using absolute value symbols.

College Algebra (MindTap Course List)

The paper referenced in the previous exercise also had the 50 taxi drivers drive in the simulator while sending...

Introduction To Statistics And Data Analysis

In Exercises 926. use the given information to draw a right triangle labeled like the one shown in Figure 8.89....

Mathematics: A Practical Odyssey

The following table reports prices and usage quantities for two items in 2009 and 2011. a. Compute price relati...

Statistics for Business & Economics, Revised (MindTap Course List)

Solve each of the following equations using the addition principle of equality. Check each answer. 47=R36

Mathematics For Machine Technology

Show the five-number summary and the box plot for the following data: 5, 15, 18, 10, 8, 12, 16, 10, 6.

STATISTICS F/BUSINESS+ECONOMICS-TEXT

In addition to the key words, you should be able to define each of the following terms: literature search title...

Research Methods for the Behavioral Sciences (MindTap Course List)

A psychologist determined that the number of sessions required to obtain the trust ofa new patient is either 1,...

Essentials Of Statistics For Business & Economics

Construct circuits for the Boolean expressions in 13-17. (PQ)V~R

Discrete Mathematics With Applications

2. In a completely randomized design, seven experimental units were used for each of the five levels of the fac...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

Write the first four terms of the arithmetic sequence whose nth term is 3n1. Then find the common difference be...

College Algebra

The World Bank records the prevalence of HIV In countries around the world. According to their data. “Prevalenc...

Introductory Statistics

[T] The function H(t)=8sin(6t) models the height H (in feet) of the tide f hours after midnight. Assume that t ...

Calculus Volume 1

In the following exercises, find the antiderivative using the indicated substitution. 262. ( x+1)5dx;u=x1

Calculus Volume 2

Reminder Round all answers to two decimal places unless otherwise indicated. Solving Exponential EquationsIn Ex...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

In Problems 17-32 use the procedures developed in this chapter to find the general solution of each differentia...

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.