
CHEMISTRY: ATOMS FIRST VOL 1 W/CONNECT
14th Edition
ISBN: 9781259327933
Author: Burdge
Publisher: MCG
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 3, Problem 3.91QP
A 3s orbital is illustrated here. Using this as a reference to show the relative size of the other four orbitals, answer the following questions.
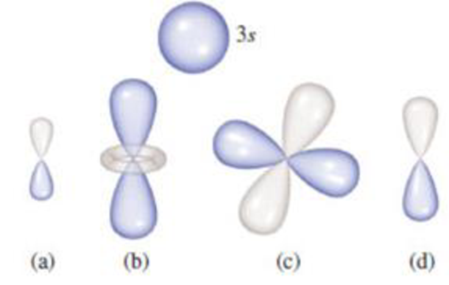
(a) Which orbital has the greatest value of n? (b) How many orbitals have a value of ℓ = 1? (c) How many other orbitals with the same value of n would have the same general shape as orbital (b)?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
CHEMISTRY: ATOMS FIRST VOL 1 W/CONNECT
Ch. 3.1 - Calculate the kinetic energy of a helium atom...Ch. 3.1 - Calculate the energy in joules of a 5.25-g object...Ch. 3.1 - Prob. 1PPBCh. 3.1 - Prob. 1PPCCh. 3.1 - Prob. 3.2WECh. 3.1 - How much greater is the electrostatic potential...Ch. 3.1 - What must the separation between charges of +2 and...Ch. 3.1 - Prob. 2PPCCh. 3.1 - Prob. 3.1.1SRCh. 3.1 - Prob. 3.1.2SR
Ch. 3.1 - Prob. 3.1.3SRCh. 3.2 - One type of laser used in the treatment of...Ch. 3.2 - What is the wavelength (in meters) of an...Ch. 3.2 - What is the frequency (in reciprocal seconds) of...Ch. 3.2 - Which of the following sets of waves best...Ch. 3.2 - Prob. 3.2.1SRCh. 3.2 - Prob. 3.2.2SRCh. 3.2 - Prob. 3.2.3SRCh. 3.2 - Prob. 3.2.4SRCh. 3.3 - Calculate the energy (in joules) of (a) a photon...Ch. 3.3 - Calculate the energy (in joules) of (a) a photon...Ch. 3.3 - (a) Calculate the wavelength (in nanometers) of...Ch. 3.3 - Prob. 3.3.1SRCh. 3.3 - Prob. 3.3.2SRCh. 3.3 - Prob. 3.3.3SRCh. 3.3 - Prob. 3.3.4SRCh. 3.3 - Prob. 3.3.5SRCh. 3.4 - Calculate the wavelength (in nanometers) of the...Ch. 3.4 - What is the wavelength (in nanometers) of a photon...Ch. 3.4 - What is the value of ni for an electron that emits...Ch. 3.4 - For each pair of transitions, determine which one...Ch. 3.4 - Prob. 3.4.1SRCh. 3.4 - Prob. 3.4.2SRCh. 3.4 - Prob. 3.4.3SRCh. 3.4 - Prob. 3.4.4SRCh. 3.5 - Calculate the de Broglie wavelength of the...Ch. 3.5 - Calculate the de Broglie wavelength (in...Ch. 3.5 - Use Equation 3.11 to calculate the momentum, p...Ch. 3.5 - Consider the impact of early electron diffraction...Ch. 3.5 - Prob. 3.5.1SRCh. 3.5 - Prob. 3.5.2SRCh. 3.5 - Prob. 3.5.3SRCh. 3.6 - An electron in a hydrogen atom is known to have a...Ch. 3.6 - Prob. 7PPACh. 3.6 - (a) Calculate the minimum uncertainty in the...Ch. 3.6 - Using Equation 3.13, we can calculate the minimum...Ch. 3.6 - Prob. 3.6.1SRCh. 3.6 - Prob. 3.6.2SRCh. 3.7 - What are the possible values for the magnetic...Ch. 3.7 - Prob. 8PPACh. 3.7 - Prob. 8PPBCh. 3.7 - Prob. 8PPCCh. 3.7 - Prob. 3.7.1SRCh. 3.7 - Prob. 3.7.2SRCh. 3.7 - Prob. 3.7.3SRCh. 3.7 - Prob. 3.7.4SRCh. 3.8 - Prob. 3.9WECh. 3.8 - Prob. 9PPACh. 3.8 - Prob. 9PPBCh. 3.8 - Prob. 9PPCCh. 3.8 - Prob. 3.8.1SRCh. 3.8 - Prob. 3.8.2SRCh. 3.8 - Prob. 3.8.3SRCh. 3.8 - Prob. 3.8.4SRCh. 3.9 - Write the electron configuration and give the...Ch. 3.9 - Prob. 10PPACh. 3.9 - Write the electron configuration and give the...Ch. 3.9 - Prob. 10PPCCh. 3.9 - Prob. 3.9.1SRCh. 3.9 - Prob. 3.9.2SRCh. 3.9 - Prob. 3.9.3SRCh. 3.10 - Without referring to Figure 3.26, write the...Ch. 3.10 - Prob. 11PPACh. 3.10 - Prob. 11PPBCh. 3.10 - Consider again the alternate universe and its...Ch. 3.10 - Prob. 3.10.1SRCh. 3.10 - Prob. 3.10.2SRCh. 3.10 - Prob. 3.10.3SRCh. 3.10 - Prob. 3.10.4SRCh. 3 - Define these terms: potential energy, kinetic...Ch. 3 - What are the units for energy commonly employed in...Ch. 3 - A truck initially traveling at 60 km/h is brought...Ch. 3 - Describe the interconversions of forms of energy...Ch. 3 - Prob. 3.5QPCh. 3 - Prob. 3.6QPCh. 3 - Prob. 3.7QPCh. 3 - Prob. 3.8QPCh. 3 - Prob. 3.9QPCh. 3 - (a) How much greater is the electrostatic energy...Ch. 3 - Prob. 3.11QPCh. 3 - Prob. 3.12QPCh. 3 - List the types of electromagnetic radiation,...Ch. 3 - Prob. 3.14QPCh. 3 - Prob. 3.15QPCh. 3 - Prob. 3.16QPCh. 3 - The SI unit of time is the second, which is...Ch. 3 - Prob. 3.18QPCh. 3 - Prob. 3.19QPCh. 3 - Four waves represent light in four different...Ch. 3 - Prob. 3.21QPCh. 3 - Prob. 3.22QPCh. 3 - Prob. 3.23QPCh. 3 - What is a photon? What role did Einsteins...Ch. 3 - A photon has a wavelength of 705 nm. Calculate the...Ch. 3 - The blue color of the sky results from the...Ch. 3 - A photon has a frequency of 6.5 109 Hz. (a)...Ch. 3 - Prob. 3.28QPCh. 3 - Prob. 3.29QPCh. 3 - Prob. 3.30QPCh. 3 - Prob. 3.31QPCh. 3 - A particular form of electromagnetic radiation has...Ch. 3 - Photosynthesis makes use of visible light to bring...Ch. 3 - The retina of a human eye can detect light when...Ch. 3 - Prob. 3.35QPCh. 3 - The binding energy of magnesium metal is 5.86 ...Ch. 3 - What is the kinetic energy of the ejected electron...Ch. 3 - A red light was shined onto a metal sample and the...Ch. 3 - A photoelectric experiment was performed by...Ch. 3 - Which of the following best explains why we see...Ch. 3 - One way to see the emission spectrum of hydrogen...Ch. 3 - How many lines would we see in the emission...Ch. 3 - For a hydrogen atom in which the electron has been...Ch. 3 - Prob. 3.40QPCh. 3 - Prob. 3.41QPCh. 3 - Briefly describe Bohrs theory of the hydrogen atom...Ch. 3 - Explain the meaning of the negative sign in...Ch. 3 - Consider the following energy levels of a...Ch. 3 - Prob. 3.45QPCh. 3 - Calculate the wavelength (in nanometers) of a...Ch. 3 - Calculate the frequency (hertz) and wavelength...Ch. 3 - What wavelength of light is needed to excite the...Ch. 3 - An electron in the hydrogen atom makes a...Ch. 3 - Explain why elements produce their own...Ch. 3 - Some copper-containing substances emit green light...Ch. 3 - Prob. 3.52QPCh. 3 - Prob. 3.53QPCh. 3 - Prob. 3.54QPCh. 3 - Why is Equation 3.11 meaningful only for...Ch. 3 - Prob. 3.56QPCh. 3 - Thermal neutrons are neutrons that move at speeds...Ch. 3 - Protons can be accelerated to speeds near that of...Ch. 3 - Prob. 3.59QPCh. 3 - Prob. 3.60QPCh. 3 - Prob. 3.61QPCh. 3 - Prob. 3.62QPCh. 3 - What are the inadequacies of Bohrs theory?Ch. 3 - What is the Heisenberg uncertainty principle? What...Ch. 3 - Prob. 3.65QPCh. 3 - Prob. 3.66QPCh. 3 - Prob. 3.67QPCh. 3 - The speed of a thermal neutron (see Problem 3.57)...Ch. 3 - Alveoli are tiny sacs of air in the lungs. Their...Ch. 3 - In the beginning of the twentieth century, some...Ch. 3 - Suppose that photons of blue light (430 nm) are...Ch. 3 - Prob. 3.72QPCh. 3 - Prob. 3.73QPCh. 3 - Which of the four quantum numbers (n, , m, ms)...Ch. 3 - Prob. 3.75QPCh. 3 - Prob. 3.76QPCh. 3 - Prob. 3.77QPCh. 3 - Prob. 3.78QPCh. 3 - Describe the shapes of s, p, and d orbitals. How...Ch. 3 - Prob. 3.80QPCh. 3 - Describe the characteristics of an s orbital, p...Ch. 3 - Why is a boundary surface diagram useful in...Ch. 3 - Prob. 3.83QPCh. 3 - Give the values of the four quantum numbers of an...Ch. 3 - Describe how a 1s orbital and a 2s orbital are...Ch. 3 - Prob. 3.86QPCh. 3 - Prob. 3.87QPCh. 3 - Make a chart of all allowable orbitals in the...Ch. 3 - Prob. 3.89QPCh. 3 - Prob. 3.90QPCh. 3 - A 3s orbital is illustrated here. Using this as a...Ch. 3 - Prob. 3.92QPCh. 3 - Prob. 3.93QPCh. 3 - State the Aufbau principle, and explain the role...Ch. 3 - Indicate the total number of (a) p electrons in N...Ch. 3 - Calculate the total number of electrons that can...Ch. 3 - Determine the total number of electrons that can...Ch. 3 - Determine the maximum number of electrons that can...Ch. 3 - Prob. 3.99QPCh. 3 - The electron configuration of an atom in the...Ch. 3 - List the following atoms in order of increasing...Ch. 3 - Determine the number of unpaired electrons in each...Ch. 3 - Determine the number of impaired electrons in each...Ch. 3 - Determine the number of unpaired electrons in each...Ch. 3 - Prob. 3.105QPCh. 3 - Portions of orbital diagrams representing the...Ch. 3 - Prob. 3.107QPCh. 3 - Prob. 3.108QPCh. 3 - Prob. 3.109QPCh. 3 - Define the following terms and give an example of...Ch. 3 - Explain why the ground-state electron...Ch. 3 - Write the election configuration of a xenon core.Ch. 3 - Comment on the correctness of the following...Ch. 3 - Prob. 3.114QPCh. 3 - Prob. 3.115QPCh. 3 - Write the ground-state electron configurations for...Ch. 3 - Write the ground-state electron configurations for...Ch. 3 - What is the symbol of the element with the...Ch. 3 - Prob. 3.119QPCh. 3 - Prob. 3.120QPCh. 3 - Discuss the current view of the correctness of the...Ch. 3 - Distinguish carefully between the following terms:...Ch. 3 - What is the maximum number of electrons in an atom...Ch. 3 - Prob. 3.124QPCh. 3 - Prob. 3.125QPCh. 3 - A baseball pitchers fastball has been clocked at...Ch. 3 - A ruby laser produces radiation of wavelength 633...Ch. 3 - Four atomic energy levels of an atom are shown...Ch. 3 - Prob. 3.129QPCh. 3 - Spectral lines of the Lyman and Balmer series do...Ch. 3 - Only a fraction of the electric energy supplied to...Ch. 3 - The figure here illustrates a series of...Ch. 3 - When one of heliums electrons is removed, the...Ch. 3 - The retina of a human eye can detect light when...Ch. 3 - An electron in an excited state in a hydrogen atom...Ch. 3 - Prob. 3.136QPCh. 3 - The election configurations described in this...Ch. 3 - Draw the shapes (boundary surfaces) of the...Ch. 3 - Prob. 3.139QPCh. 3 - Consider the graph here. (a) Calculate the binding...Ch. 3 - Scientists have found interstellar hydrogen atoms...Ch. 3 - Ionization energy is the minimum energy required...Ch. 3 - Prob. 3.143QPCh. 3 - Prob. 3.144QPCh. 3 - The cone cells of the human eye are sensitive to...Ch. 3 - (a) An electron in the ground state of the...Ch. 3 - Prob. 3.147QPCh. 3 - Prob. 3.148QPCh. 3 - When an election makes a transition between energy...Ch. 3 - Blackbody radiation is the term used to describe...Ch. 3 - Suppose that photons of red light (675 nm) are...Ch. 3 - In an election microscope, electrons are...Ch. 3 - According to Einsteins special theory of...Ch. 3 - The mathematical equation for studying the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, chemistry and related others by exploring similar questions and additional content below.Similar questions
- Which of the following sets of quantum numbers correctly represents a 4p orbital? (a) n = 4, = 0, m = 1 (b) n = 4, = 1, m = 0 (c) n = 4, = 2, m = 1 (d) n = 4, = 1, m =2arrow_forwardWhat is the maximum number of electrons that can occupy a f subshell (l = 3)?arrow_forward6.96 When a helium atom absorbs light at 58.44 nm, an electron is promoted from the 1s orbital to a 2p orbital. Given that the ionization energy of (ground state) helium is 2372 kJ/ mol, find the longest wavelength of light that could eject an electron from the excited state helium atom.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781337399074Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning
Chemistry & Chemical ReactivityChemistryISBN:9781133949640Author:John C. Kotz, Paul M. Treichel, John Townsend, David TreichelPublisher:Cengage Learning Introductory Chemistry: An Active Learning Approa...ChemistryISBN:9781305079250Author:Mark S. Cracolice, Ed PetersPublisher:Cengage Learning
Introductory Chemistry: An Active Learning Approa...ChemistryISBN:9781305079250Author:Mark S. Cracolice, Ed PetersPublisher:Cengage Learning Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStaxChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co
Chemistry by OpenStax (2015-05-04)ChemistryISBN:9781938168390Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark BlaserPublisher:OpenStaxChemistry: Matter and ChangeChemistryISBN:9780078746376Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl WistromPublisher:Glencoe/McGraw-Hill School Pub Co Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning
Chemistry for Engineering StudentsChemistryISBN:9781337398909Author:Lawrence S. Brown, Tom HolmePublisher:Cengage Learning

Chemistry & Chemical Reactivity
Chemistry
ISBN:9781337399074
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning

Chemistry & Chemical Reactivity
Chemistry
ISBN:9781133949640
Author:John C. Kotz, Paul M. Treichel, John Townsend, David Treichel
Publisher:Cengage Learning

Introductory Chemistry: An Active Learning Approa...
Chemistry
ISBN:9781305079250
Author:Mark S. Cracolice, Ed Peters
Publisher:Cengage Learning

Chemistry by OpenStax (2015-05-04)
Chemistry
ISBN:9781938168390
Author:Klaus Theopold, Richard H Langley, Paul Flowers, William R. Robinson, Mark Blaser
Publisher:OpenStax

Chemistry: Matter and Change
Chemistry
ISBN:9780078746376
Author:Dinah Zike, Laurel Dingrando, Nicholas Hainen, Cheryl Wistrom
Publisher:Glencoe/McGraw-Hill School Pub Co

Chemistry for Engineering Students
Chemistry
ISBN:9781337398909
Author:Lawrence S. Brown, Tom Holme
Publisher:Cengage Learning
Quantum Numbers, Atomic Orbitals, and Electron Configurations; Author: Professor Dave Explains;https://www.youtube.com/watch?v=Aoi4j8es4gQ;License: Standard YouTube License, CC-BY
QUANTUM MECHANICAL MODEL/Atomic Structure-21E; Author: H to O Chemistry;https://www.youtube.com/watch?v=mYHNUy5hPQE;License: Standard YouTube License, CC-BY