
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
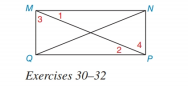
Chapter 3.2, Problem 32E
In Exercises 30 to 32, draw the
| Given: |
|
| Prove: |
|
| (HINT: Show
|
|
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 3 Solutions
Elementary Geometry for College Students
Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4. consider the congruent...Ch. 3.1 - In Exercises 1 to 4, consider the congruent...Ch. 3.1 - Consider ABC and ABD in the figure shown. By the...Ch. 3.1 - In a right triangle, the sides that form the right...Ch. 3.1 - In ABC, the midpoints of the sides are joined. a...Ch. 3.1 - a. Suppose that you wish to prove that RSTSRV....Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...
Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 9 to 12, congruent parts are...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 13 to 18, use only the given...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 19 and 20, the triangles to be proved...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 21 to 24, the triangles named can be...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 25 and 26, complete each proof. Use...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 27 to 32, use SSS, SAS, ASA, or AAS...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the methods to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In Exercises 33 to 36, the method to be used are...Ch. 3.1 - In quadrilateral ABCD, AC and BD are perpendicular...Ch. 3.1 - In ABC and DEF, you know that AD, CF, and ABDE....Ch. 3.1 - Prob. 39ECh. 3.1 - In Exercises 39 to 40, complete each proof. Given:...Ch. 3.1 - Given: ABC; RS is the perpendicular bisector of...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercises 1 to 4, state the reason SSS, SAS,...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 9ECh. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - In Exercise 5 to 12, plan and write the two-column...Ch. 3.2 - Prob. 13ECh. 3.2 - Prob. 14ECh. 3.2 - Given: HJ bisects KHL HJKL See figure for exercise...Ch. 3.2 - Given: HJ bisects KHL HJKL In Exercise 15, you cam...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 17 to 20, first prove that triangles...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 21 to 26, ABC is a right triangle. Use...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - In Exercise 27 to 29, prove the indicated...Ch. 3.2 - Prob. 30ECh. 3.2 - Prob. 31ECh. 3.2 - In Exercises 30 to 32, draw the triangles that are...Ch. 3.2 - Given: RW bisects SRU Prove: RSRU TRUVRS HINT:...Ch. 3.2 - Given: DBBC and CEDE Prove: ABAE BDCECD HINT:...Ch. 3.2 - In the roof truss shown, AB=8 and mHAF=37. Find: a...Ch. 3.2 - In the support system of the bridge shown, AC=6ft...Ch. 3.2 - As a car moves along the roadway in a mountain...Ch. 3.2 - Because of the construction along the road from A...Ch. 3.2 - Given: Regular pentagon ABCDE with diagonals BE...Ch. 3.2 - In the figure with regular pentagon ABCDE, do BE...Ch. 3.3 - For Exercises 1 to 8, use the accompanying...Ch. 3.3 - Prob. 2ECh. 3.3 - Prob. 3ECh. 3.3 - Prob. 4ECh. 3.3 - Prob. 5ECh. 3.3 - For Exercises 1 to 8, use the accompanying...Ch. 3.3 - Prob. 7ECh. 3.3 - Prob. 8ECh. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - Prob. 10ECh. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - In Exercises 9 to 12, determine whether the sets...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - Prob. 14ECh. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - In Exercises 13 to 18, describe the line segments...Ch. 3.3 - Prob. 18ECh. 3.3 - Prob. 19ECh. 3.3 - Is it possible for a triangle to be: a an acute...Ch. 3.3 - Prob. 21ECh. 3.3 - In concave quadrilateral ABCD, the angle at A...Ch. 3.3 - Prob. 23ECh. 3.3 - Prob. 24ECh. 3.3 - Prob. 25ECh. 3.3 - Prob. 26ECh. 3.3 - Prob. 27ECh. 3.3 - Prob. 28ECh. 3.3 - Prob. 29ECh. 3.3 - Prob. 30ECh. 3.3 - Prob. 31ECh. 3.3 - Prob. 32ECh. 3.3 - Suppose that ABCDEF. Also, AX bisects CAB and DY...Ch. 3.3 - Suppose that ABCDEF. Also, AX is the median from A...Ch. 3.3 - In Exercises 35 and 36, complete each proof using...Ch. 3.3 - Prob. 36ECh. 3.3 - Prob. 37ECh. 3.3 - Prob. 38ECh. 3.3 - Prob. 39ECh. 3.3 - In isosceles triangle BAT, ABAT.Also, BRBTAR, if...Ch. 3.3 - Prob. 41ECh. 3.3 - Prob. 42ECh. 3.3 - Prob. 43ECh. 3.3 - Prob. 44ECh. 3.3 - Prob. 45ECh. 3.3 - Prob. 46ECh. 3.3 - Given: In the figure, XZYZ and Z is the midpoint...Ch. 3.3 - Prob. 48ECh. 3.4 - In Exercises 1 to 6, use line segments of given...Ch. 3.4 - Prob. 2ECh. 3.4 - Prob. 3ECh. 3.4 - Prob. 4ECh. 3.4 - Prob. 5ECh. 3.4 - Prob. 6ECh. 3.4 - Prob. 7ECh. 3.4 - Prob. 8ECh. 3.4 - Prob. 9ECh. 3.4 - Prob. 10ECh. 3.4 - Prob. 11ECh. 3.4 - Prob. 12ECh. 3.4 - In Exercises 13 and 14. use the angles and lengths...Ch. 3.4 - Prob. 14ECh. 3.4 - Prob. 15ECh. 3.4 - Prob. 16ECh. 3.4 - Prob. 17ECh. 3.4 - Prob. 18ECh. 3.4 - Prob. 19ECh. 3.4 - Prob. 20ECh. 3.4 - Prob. 21ECh. 3.4 - Prob. 22ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 24ECh. 3.4 - In Exercises 23 to 26, use line segments of length...Ch. 3.4 - Prob. 26ECh. 3.4 - In Exercise 27 and 28, use the given angle R and...Ch. 3.4 - Prob. 28ECh. 3.4 - Complete the justification of the construction of...Ch. 3.4 - Prob. 30ECh. 3.4 - Prob. 31ECh. 3.4 - Prob. 32ECh. 3.4 - Prob. 33ECh. 3.4 - Prob. 34ECh. 3.4 - Prob. 35ECh. 3.4 - Draw a right triangle and construct the angle...Ch. 3.4 - Draw an obtuse triangle and construct the three...Ch. 3.4 - Prob. 38ECh. 3.4 - A carpenter has placed a square over an angle in...Ch. 3.4 - Prob. 40ECh. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - In Exercise 1 to 10, classify each statement as...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose angles...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Is it possible to draw a triangle whose sides...Ch. 3.5 - Prob. 15ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Prob. 17ECh. 3.5 - In Exercises 15 to 18, describe the triangle XYZ ,...Ch. 3.5 - Two of the sides of an isosceles triangle have...Ch. 3.5 - The sides of a right triangle have lengths of 6cm,...Ch. 3.5 - Prob. 21ECh. 3.5 - One of the angles of an isosceles triangle...Ch. 3.5 - Prob. 23ECh. 3.5 - A tornado has just struck a small Kansas community...Ch. 3.5 - In Exercises 25 and 26, complete each proof shown...Ch. 3.5 - Prob. 26ECh. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - In Exercises 27 and 28, construct proofs. Given:...Ch. 3.5 - Prob. 29ECh. 3.5 - In MNP not shown, point Q lies on NP so that MQ...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prob. 33ECh. 3.5 - In Exercises 31 to 34, apply a form of Theorem...Ch. 3.5 - Prove by the indirect method: Given: MPN is not...Ch. 3.5 - Prove by the indirect method: Given: Scalene XYZ...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.5 - In Exercises 37 and 38, prove each theorem. The...Ch. 3.CR - Given: AEBDEC AEDE Prove: AEBDECCh. 3.CR - Given: ABEFACDF12 Prove: BECh. 3.CR - Given: AD bisects BC ABBCDCBC Prove: AEDECh. 3.CR - Prob. 4CRCh. 3.CR - Prob. 5CRCh. 3.CR - Given: B is the midpoint of AC BDAC Prove: ADC is...Ch. 3.CR - Prob. 7CRCh. 3.CR - Prob. 8CRCh. 3.CR - Given: YZ is the base of an isosceles triangle;...Ch. 3.CR - Prob. 10CRCh. 3.CR - Prob. 11CRCh. 3.CR - Prob. 12CRCh. 3.CR - Prob. 13CRCh. 3.CR - Given: AC bisects BAD Prove: ADCDCh. 3.CR - Prob. 15CRCh. 3.CR - Prob. 16CRCh. 3.CR - Prob. 17CRCh. 3.CR - Name the longest line segment shown in...Ch. 3.CR - Prob. 19CRCh. 3.CR - Two sides of a triangle have lengths 15 and 20....Ch. 3.CR - Prob. 21CRCh. 3.CR - Prob. 22CRCh. 3.CR - Prob. 23CRCh. 3.CR - Prob. 24CRCh. 3.CR - Given: ABC is isosceles with base AB...Ch. 3.CR - Prob. 26CRCh. 3.CR - Prob. 27CRCh. 3.CR - Construct a right triangle that has acute angle A...Ch. 3.CR - Construct a second isosceles triangle in which the...Ch. 3.CT - It is given that ABCDEF triangles not shown a If...Ch. 3.CT - Consider XYZ triangles not shown a Which side is...Ch. 3.CT - Prob. 3CTCh. 3.CT - Prob. 4CTCh. 3.CT - With congruent parts marked, are the two triangles...Ch. 3.CT - Prob. 6CTCh. 3.CT - Prob. 7CTCh. 3.CT - CM is the median for ABC from vertex C to side AB....Ch. 3.CT - Prob. 9CTCh. 3.CT - Prob. 10CTCh. 3.CT - Prob. 11CTCh. 3.CT - Show all arcs in the following construction....Ch. 3.CT - Prob. 13CTCh. 3.CT - Prob. 14CTCh. 3.CT - Prob. 15CTCh. 3.CT - Prob. 16CTCh. 3.CT - Complete all statements and reasons for the...Ch. 3.CT - Complete all missing statements and reasons in the...Ch. 3.CT - The perimeter of an isosceles triangle is 32cm. If...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- In Exercises 27 to 32, use SSS, SAS, ASA, or AAS to prove that the triangles are congruent. Given: PN bisects MQ M and Q are right angles Prove: PQRNMRarrow_forwardIn Exercises 17 to 24, complete each proof. Given: MNNP,QRRP Prove: MNPQRP Exercises 17, 18 PROOF Statements Reasons 1. ? 1. ? 2. sN and QRP are right s 2. ? 3. ? 3. All right s are 4. PP 4. ? 5. ? 5.?arrow_forwardIn Exercises 21 to 24, the triangles named can be proved congruent. Considering the congruent pairs marked, name the additional pair of parts that must be congruent in order to use the method named. AAS EFGJHGarrow_forward
- In Exercise 30 to 32, draw the triangle that is to be shown congruent separately. Then complete the proof. Given: MQP and NPQ are right s MQNP Prove: MPNQ HINT:Show MQPNPQarrow_forwardIn Exercises 1 to 4, state the reason SSS, SAS, ASA, AAS, or HL why the triangles are congruent. Given: P is the midpoint of MR and NQ. Prove: MNPQRParrow_forwardIn Exercises 27 to 32, use SSS, SAS, ASA, or AAS to prove that the triangles are congruent. Given: PQ bisects MPN MPNP Prove: MQPNQParrow_forward
- In Exercises 21 to 24, the triangles named can be proved congruent. Considering the congruent pairs marked, name the additional pair of parts that must be congruent in order to use the method named. SSS MNOOPMarrow_forwardIn Exercises 1 to 6, state the hypothesis H and the conclusion C for each statement. If two sides of a triangle are congruent, then the triangle is isosceles.arrow_forwardIn Exercises 19 to24 , complete each proof. Given: M-Q-T and P-Q-R such that MNPQ and QRST are s Prove: NSarrow_forward
- In Exercises 27 to 32, use SSS, SAS, ASA, or AAS to prove that the triangles are congruent. Given: PQMN and 12 Prove: MQPNQParrow_forwardIn Exercises 9 to 12, congruent parts are indicated by like dashes sides or arcs angles. State which method SSS, SAS. ASA, or AAS would be used to prove the two triangles congruent.arrow_forwardIn Exercises 19 to 24, complete each proof. Given: 12and34 Prove: MNPQ is a kite PROOF Statements Reasons 1. 12and34 1. ? 2. NQNQ 2. ? 3. ? 3. ASA 4. MNPN and MQPQ 4. ? 5. ? 5. If a quadrilateral has two pairs of adjacent sides, it is a kitearrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
What are the Different Types of Triangles? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=1k0G-Y41jRA;License: Standard YouTube License, CC-BY
Law of Sines AAS, ASA, SSA Ambiguous Case; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=FPVGb-yWj3s;License: Standard YouTube License, CC-BY
Introduction to Statistics..What are they? And, How Do I Know Which One to Choose?; Author: The Doctoral Journey;https://www.youtube.com/watch?v=HpyRybBEDQ0;License: Standard YouTube License, CC-BY
Triangles | Mathematics Grade 5 | Periwinkle; Author: Periwinkle;https://www.youtube.com/watch?v=zneP1Q7IjgQ;License: Standard YouTube License, CC-BY
What Are Descriptive Statistics And Inferential Statistics?; Author: Amour Learning;https://www.youtube.com/watch?v=MUyUaouisZE;License: Standard Youtube License