Introduction to Electrodynamics
4th Edition
ISBN: 9781108420419
Author: David J. Griffiths
Publisher: Cambridge University Press
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Textbook Question
Chapter 3.3, Problem 3.16P
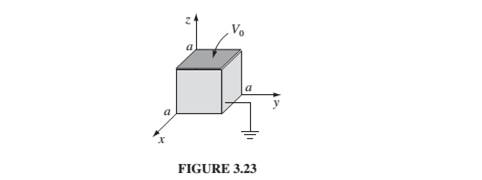
A cubical box (sides of length a) consists of five metal plates, whichare welded together and grounded (Fig. 3.23). The top is made of a separate sheetof metal, insulated from the others, and held at a constant potential
Expert Solution & Answer
Trending nowThis is a popular solution!
Learn your wayIncludes step-by-step video
schedule10:43
Students have asked these similar questions
Determine whether the vector field is conservative and, if so, find the general potential function.
F=⟨cos(z),2y^3,−xsin(z)⟩
A thin plastic rod of length L has a positive charge Q uniformly distributed along its length. We willcalculate the exact field due to the rod in the next homework set. In this set, we will approximatethe rod as several point sources and develop the Riemann sum as an intermediate step on the wayto writing an integral.For those aiming at a P rating, you may use L = 3.0m , Q = 17 mC, and y = 0.11m to calculate theanswer numerically first and substitute variables for them only as required in the problem statement.For those aiming at an E rating, leave L, Q and y as variables. Substitute numbers only whererequired in the problem statement, and only as a last step
Show that electric potential for a shell whose radius is R, has charge q uniformly distributed on its entire surface, is the same as electric potential for a conductor (Solid) has radius R and charge q.
Chapter 3 Solutions
Introduction to Electrodynamics
Ch. 3.1 - Find the average potential over a spherical...Ch. 3.1 - Prob. 3.2PCh. 3.1 - Prob. 3.3PCh. 3.1 - Prob. 3.4PCh. 3.1 - Prob. 3.5PCh. 3.1 - Prob. 3.6PCh. 3.2 - Find the force on the charge +q in Fig. 3.14....Ch. 3.2 - (a) Using the law of cosines, show that Eq. 3.17...Ch. 3.2 - In Ex. 3.2 we assumed that the conducting sphere...Ch. 3.2 - A uniform line charge is placed on an infinite...
Ch. 3.2 - Two semi-infinite grounded conducting planes meet...Ch. 3.2 - Prob. 3.12PCh. 3.3 - Find the potential in the infinite slot of Ex. 3.3...Ch. 3.3 - Prob. 3.14PCh. 3.3 - A rectangular pipe, running parallel to the z-axis...Ch. 3.3 - A cubical box (sides of length a) consists of five...Ch. 3.3 - Prob. 3.17PCh. 3.3 - Prob. 3.18PCh. 3.3 - Prob. 3.19PCh. 3.3 - Suppose the potential V0() at the surface of a...Ch. 3.3 - Prob. 3.21PCh. 3.3 - In Prob. 2.25, you found the potential on the axis...Ch. 3.3 - Prob. 3.23PCh. 3.3 - Prob. 3.24PCh. 3.3 - Find the potential outside an infinitely long...Ch. 3.3 - Prob. 3.26PCh. 3.4 - A sphere of radius R, centered at the origin,...Ch. 3.4 - Prob. 3.28PCh. 3.4 - Four particles (one of charge q, one of charge 3q,...Ch. 3.4 - In Ex. 3.9, we derived the exact potential for a...Ch. 3.4 - Prob. 3.31PCh. 3.4 - Two point charges, 3qand q , arc separated by a...Ch. 3.4 - Prob. 3.33PCh. 3.4 - Three point charges are located as shown in Fig....Ch. 3.4 - A solid sphere, radius R, is centered at the...Ch. 3.4 - Prob. 3.36PCh. 3.4 - Prob. 3.37PCh. 3.4 - Here’s an alternative derivation of Eq. 3.10 (the...Ch. 3.4 - Prob. 3.39PCh. 3.4 - Two long straight wires, carrying opposite uniform...Ch. 3.4 - Prob. 3.41PCh. 3.4 - You can use the superposition principle to combine...Ch. 3.4 - A conducting sphere of radius a, at potential V0 ,...Ch. 3.4 - Prob. 3.44PCh. 3.4 - Prob. 3.45PCh. 3.4 - A thin insulating rod, running from z=a to z=+a ,...Ch. 3.4 - Prob. 3.47PCh. 3.4 - Prob. 3.48PCh. 3.4 - Prob. 3.49PCh. 3.4 - Prob. 3.50PCh. 3.4 - Prob. 3.51PCh. 3.4 - Prob. 3.52PCh. 3.4 - Prob. 3.53PCh. 3.4 - Prob. 3.54PCh. 3.4 - Prob. 3.55PCh. 3.4 - Prob. 3.56PCh. 3.4 - Prob. 3.57PCh. 3.4 - Find the charge density () on the surface of a...
Additional Science Textbook Solutions
Find more solutions based on key concepts
(I) Calculate the force needed to move the wire in Fig. 13–35 if it is immersed in a soapy solution and the wir...
Physics for Scientists and Engineers with Modern Physics
A nurse pushes a cart by exerting a force on the handle at a downward angle 35.0° below the horizontal. The loa...
College Physics
The table below shows the ratio of peak voltage to peak currentthat is, the impedance Zas a function of frequen...
Essential University Physics: Volume 2 (3rd Edition)
The pV-diagram of the Carnot cycle.
Sears And Zemansky's University Physics With Modern Physics
Q4.8 Some people say that the “force of inertia” (or “force of momentum”) throws the passengers forward when a ...
University Physics with Modern Physics (14th Edition)
8. (a) Does a sound level of zero decibels mean that there is no sound? (b) Is there any physical meaning to a ...
College Physics (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, physics and related others by exploring similar questions and additional content below.Similar questions
- Repeat the preceding problem, with E=2xi+3x2k.arrow_forwardUsing the Dirac-delta function, find the potential and electric field at the point (0,0,Z) of a homogeneously charged disk of radius a with total charge Q.arrow_forwardA sphere of radius R centered at the origin carries charge density ρ(r, θ) = k*(R/r^ 2) (R − 2r) sin θ where k is a constant, and r, θ are the usual spherical coordinates. Use the multipole expansion to find the approximate potential for points on the z-axis far from the sphere (z >> R).arrow_forward
- Show if the potential changes in the following relation V(r) In this case, we only have a non-circular closed path when n = -2 .arrow_forwardSince the potential of a perfect conducting sphere with a radius of 3.5 cm in empty space is 10 V, calculate the value of the potentials at a distance of 13.3 cm from the center of the sphere as Volts in ke.arrow_forwardConsider a uniformly charged ring in the xy plane, centered at the origin. The ring has radius a and positive charge q distributed evenly along its circumference. Imagine a small metal ball of mass m and negative charge −q0. The ball is released from rest at the point (0,0,d) and constrained to move along the z axis, with no damping. If 0<d≪a, what will be the ball's subsequent trajectory? repelled from the origin attracted toward the origin and coming to rest oscillating along the z axis between z=d and z=−d circling around the z axis at z=darrow_forward
- find a potential function f for the field F=e4y+3z(5i+20xj+15xk)arrow_forwardWhat is the energy required to bring a point charge ? from very far to a distance ? from the center of an insulating sphere of radius ? with charge ?, assuming uniform charge density and d > R? What if the sphere is replaced with a hollow spherical conductor of charge -Q and radius R, what would the energy required be then? Hint: you don’t have to re-derive the potential due to a charged sphere again.arrow_forwardFind the potential inside and outside a uniformly charged solid spherewhose radius is R and whose total charge is q. Use infinity as your reference point.Compute the gradient of V in each region, and check that it yields the correct field.Sketch V (r).arrow_forward
- Compute for the absolute potential for every of the following distances from a charge of 2 μC: whenr = 100 mm and r = 500 mm. How much work is needed to carry a 0.05 μC charge from the point at r =100 mm to that at r = 100 mm?arrow_forwardA proton circulates in a cyclotron, beginning approximatelyat rest at the center.Whenever it passes through the gap betweendees, the electric potential difference between the dees is 200 V.(a) By how much does its kinetic energy increase with each passagethrough the gap? (b) What is its kinetic energy as it completes100 passes through the gap? Let r100 be the radius of the proton’scircular path as it completes those 100 passes and enters a dee,and let r101 be its next radius, as it enters a dee the next time. (c) Bywhat percentage does the radius increase when it changes fromr100 to r101? That is, what is percentage increase r101 - r100/r100 100%?arrow_forwardCheck Your Understanding How would the above limit change with a uniformly rectangle instead of a disk?arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Classical Dynamics of Particles and Systems
Physics
ISBN:9780534408961
Author:Stephen T. Thornton, Jerry B. Marion
Publisher:Cengage Learning
Modern Physics
Physics
ISBN:9781111794378
Author:Raymond A. Serway, Clement J. Moses, Curt A. Moyer
Publisher:Cengage Learning
Ising model | A Bird's Eye View | Solid State Physics; Author: Pretty Much Physics;https://www.youtube.com/watch?v=1CCZkHPrhzk;License: Standard YouTube License, CC-BY