Graph of functions using logarithmic scale:

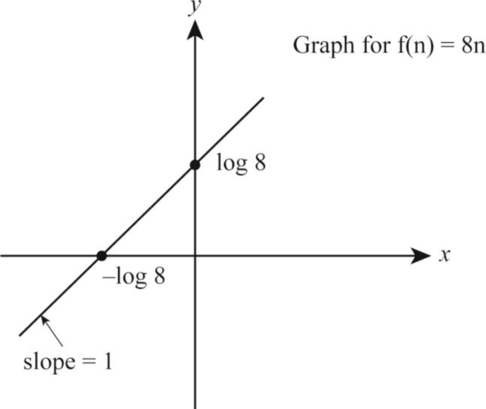
8n:

Let the function be:

$f(n)=8n$

Take the logarithm on both the sides of the above function as follows:

$log f(n) = log 8n$

$logf(n) = log n+ log 8$         (1)

According to the given data, let us take $log f(n)=Y$ , $log n= X$ . Substitute the values in Equation (1):

$Y=X+log8$         (2)

Thus, from the above Equation (2), the value of $Yinterval= log 8$ , $Xinterval =−log 8$

The following is the graph representation corresponding to the values $Yinterval= log 8$ , $Xinterval =−log 8$ on respective x-axis and y-axis respectively.

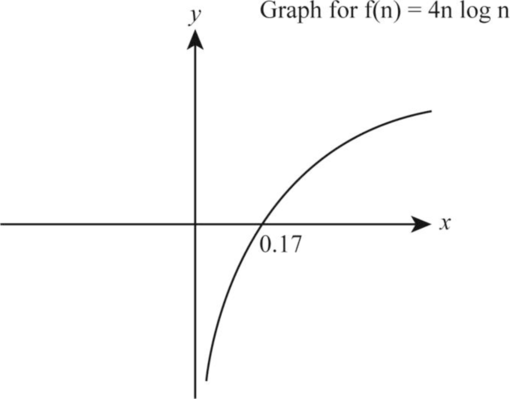
4n logn:

Let the function be:

$f(n)=4nlogn$

Take the logarithm on both the sides of the above function as follows:

$log f(n) = log 4n log n$

$logf(n) = log 4+ log (nlog n)$

$logf(n) = log 4+ log n + log(log n)$         (3)

According to the given data, let us take $log f(n)=Y$ , $log n= X$ . Substitute the values in Equation (3)

$Y=X+log(X) +log4$         (4)

The following is the graph representation corresponding for the function $f(n)=4nlogn$ on respective x-axis and y-axis respectively.

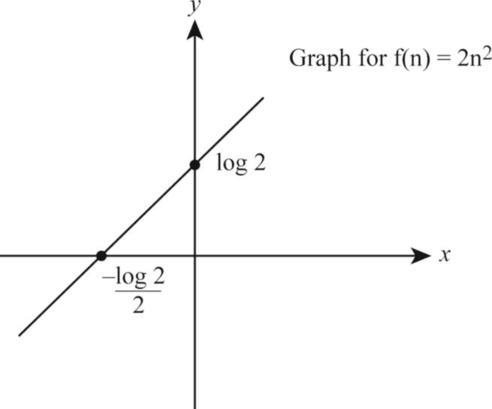
$2n2$ :

Let the function be:

$f(n)=2n2$

Take the logarithm on both the sides of the above function as follows:

$log f(n) = log 2n2$

$logf(n) = log 2+ log n2$

$logf(n) = log 2+ 2log n$         (5)

According to the given data, let us take $log f(n)=Y$ , $log n= X$ . Substitute the values in Equation (5)

$Y=2X+log2$         (6)

Thus, from the above Equation (6), the value of $Yinterval= log 2$ while substituting X =0, $Xinterval =−log 22$ while substituting Y=0.

The following is the graph representation corresponding to the values $Yinterval= log 2$ , $Xinterval =−log 22$ on respective x-axis and y-axis respectively.

$n3$ :

Let the function be:

$f(n)=n3$

Take the logarithm on both the sides of the above function as follows:

$log f(n) = log n3$

$logf(n) = 3log n$         (7)

According to the given data, let us take $log f(n)=Y$ , $log n= X$ . Substitute the values in Equation (6)

$Y=3X$         (8)

The following is the graph representation corresponding to the value on respective x-axis and y-axis respectively.

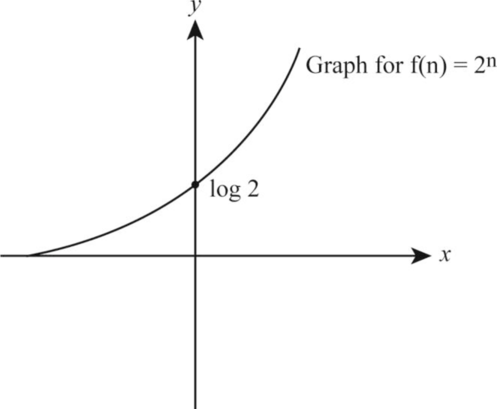
$2n$ :

Let the function be:

$f(n)= 2n$

Take the logarithm on both the sides of the above function as follows:

$log f(n) = log 2n$

$logf(n) = nlog 2$

$logf(n) = elog nlog 2$         (7)

According to the given data, let us take $log f(n)=Y$ , $log n= X$ . Substitute the values in Equation (6)

$Y= ex log2$         (8)

The following is the graph representation corresponding to the value on respective x-axis and y-axis respectively.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Chapter 3, Problem 43P

Chapter 4, Problem 2R

Students have asked these similar questions

Dijkstra's Algorithm (part 1). Consider the network shown below, and Dijkstra’s link-state algorithm. Here, we are interested in computing the least cost path from node E (note: the start node here is E) to all other nodes using Dijkstra's algorithm. Using the algorithm statement used in the textbook and its visual representation, complete the "Step 0" row in the table below showing the link state algorithm’s execution by matching the table entries (i), (ii), (iii), and (iv) with their values. Write down your final [correct] answer, as you‘ll need it for the next question.

4. |z + 5 - 5i| = 7

14. dz, C: |z❘ C: |z❘ = 0.6 ze² - 2iz H

Chapter 4 Solutions

Data Structures and Algorithms in Java

Ch. 4 - Prob. 1R Ch. 4 - The number of operations executed by algorithms A...Ch. 4 - The number of operations executed by algorithms A...Ch. 4 - Prob. 4R Ch. 4 - Prob. 5R Ch. 4 - Prob. 6R Ch. 4 - Prob. 7R Ch. 4 - Prob. 8R Ch. 4 - Prob. 9R Ch. 4 - Prob. 10R

Ch. 4 - Prob. 11R Ch. 4 - Prob. 12R Ch. 4 - Prob. 13R Ch. 4 - Prob. 14R Ch. 4 - Prob. 15R Ch. 4 - Prob. 16R Ch. 4 - Prob. 17R Ch. 4 - Prob. 18R Ch. 4 - Prob. 19R Ch. 4 - Prob. 20R Ch. 4 - Prob. 21R Ch. 4 - Prob. 22R Ch. 4 - Show that 2n+1 is O(2n).Ch. 4 - Prob. 24R Ch. 4 - Prob. 25R Ch. 4 - Prob. 26R Ch. 4 - Prob. 27R Ch. 4 - Prob. 28R Ch. 4 - Prob. 29R Ch. 4 - Prob. 30R Ch. 4 - Prob. 31R Ch. 4 - Prob. 32R Ch. 4 - Prob. 33R Ch. 4 - Prob. 34R Ch. 4 - Prob. 35C Ch. 4 - Prob. 36C Ch. 4 - Prob. 37C Ch. 4 - Prob. 38C Ch. 4 - Prob. 39C Ch. 4 - Prob. 40C Ch. 4 - Prob. 41C Ch. 4 - Prob. 42C Ch. 4 - Prob. 43C Ch. 4 - Draw a visual justification of Proposition 4.3...Ch. 4 - Prob. 45C Ch. 4 - Prob. 46C Ch. 4 - Communication security is extremely important in...Ch. 4 - Al says he can prove that all sheep in a flock are...Ch. 4 - Consider the following justification that the...Ch. 4 - Consider the Fibonacci function, F(n) (see...Ch. 4 - Prob. 51C Ch. 4 - Prob. 52C Ch. 4 - Prob. 53C Ch. 4 - Prob. 54C Ch. 4 - An evil king has n bottles of wine, and a spy has...Ch. 4 - Prob. 56C Ch. 4 - Prob. 57C Ch. 4 - Prob. 58C Ch. 4 - Prob. 59C Ch. 4 - Prob. 60P Ch. 4 - Prob. 61P Ch. 4 - Perform an experimental analysis to test the...Ch. 4 - Prob. 63P

Knowledge Booster

Learn more about

Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, computer-science and related others by exploring similar questions and additional content below.

Similar questions

SEE MORE QUESTIONS

Recommended textbooks for you

Operations Research : Applications and Algorithms
Computer Science
ISBN:9780534380588
Author:Wayne L. Winston
Publisher:Brooks Cole
Programming Logic & Design Comprehensive
Computer Science
ISBN:9781337669405
Author:FARRELL
Publisher:Cengage
C++ Programming: From Problem Analysis to Program...
Computer Science
ISBN:9781337102087
Author:D. S. Malik
Publisher:Cengage Learning
COMPREHENSIVE MICROSOFT OFFICE 365 EXCE
Computer Science
ISBN:9780357392676
Author:FREUND, Steven
Publisher:CENGAGE L
C++ for Engineers and Scientists
Computer Science
ISBN:9781133187844
Author:Bronson, Gary J.
Publisher:Course Technology Ptr
Systems Architecture
Computer Science
ISBN:9781305080195
Author:Stephen D. Burd
Publisher:Cengage Learning