Given information:
The non-linear simultaneous equation,
(x−4)2+(y−4)2=5x2+y2=16
Formula used:
The Newton-Raphson formula for two non-linear equation is,
xi+1=xi−ui∂vi∂y−vi∂ui∂y∂ui∂x∂vi∂y−∂ui∂y∂vi∂xyi+1=yi−vi∂ui∂x−ui∂vi∂x∂ui∂x∂vi∂y−∂ui∂y∂vi∂x
Calculation:
Use MATLAB to draw the graph of the equations, (x−4)2+(y−4)2=5 and x2+y2=16 as below,
Code:
clear;clc;
%x-coordinates spacing is defined.
x =linspace(-10,10,100);
%first function is defined.
y1_1 =(- x.^2+8.*x -11).^(1/2)+4;
y1_2 =4-(- x.^2+8.*x -11).^(1/2);
%second function is defined.
y2_1 =(4- x).^(1/2).*(x +4).^(1/2);
y2_2 =-(4- x).^(1/2).*(x +4).^(1/2);
Y1 =[y1_1,y1_2];
Y2 =[y2_1,y2_2];
X =[x,x];
%Plot command is used to draw the two function.
plot(X,Y1,X,Y2)
legend('(x-4)^2 + (y-4)^2 = 5','x^2 + y^2 = 16')
xlabel('x')
ylabel('y')
Output:
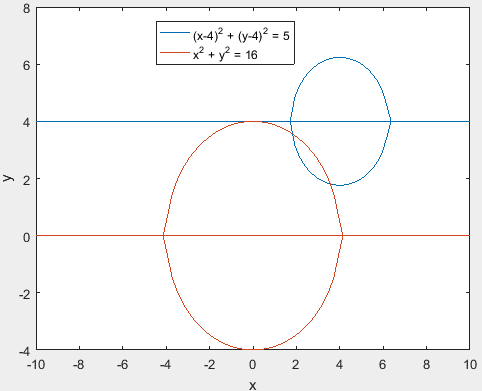
From the above graph, it is observed that there are two roots at (1.8,3.6) and (3.6,1.8).
Consider theequations,
(x−4)2+(y−4)2=5x2+y2=16
Rewrite the equation as below,
u(x,y)=5−(x−4)2−(y−4)2v(x,y)=16−x2−y2
Partial differentiate the above functions with respect to x,
∂u∂x=∂∂x[5−(x−4)2−(y−4)2]=∂∂x(5)−∂∂x[(x−4)2]−∂∂x[(y−4)2]=0−2(x−4)−0=−2x+8
And,
∂v∂x=∂∂x(16−x2−y2)=∂∂x(16)−∂∂x(x2)−∂∂x(y2)=0−2x−0=−2x
Now, partial differentiate the above functions with respect to y,
∂u∂y=∂∂y[5−(x−4)2−(y−4)2]=∂∂y(5)−∂∂y(x−4)2−∂∂y(y−4)2=0−0−2(y−4)=−2y+8
And,
∂v∂y=∂∂y(16−x2−y2)=∂∂y(16)−∂∂y(x2)−∂∂y(y2)=0−0−2y=−2y
Use initial guesses x0=1.8 and y0=3.6, the first iteration is,
x0+1=x0−u0∂v0∂y−v0∂u0∂y∂u0∂x∂v0∂y−∂u0∂y∂v0∂xx1=1.8−{5−((1.8)−4)2−((3.6)−4)2}(−2(3.6))−(16−(1.8)2−(3.6)2)(−2(3.6)+8)(−2(1.8)+8)(−2(3.6))−(−2(3.6)+8)(−2(1.8))=1.8−{5−(−2.2)2−(−0.4)2}(−7.2)−(16−3.24−12.96)(−7.2+8)(−3.6+8)(−7.2)−(−7.2+8)(−3.6)=1.8056
And,
y0+1=y0−v0∂u0∂x−u0∂v0∂x∂u0∂x∂v0∂y−∂u0∂y∂v0∂xy1=3.6−(16−(1.8)2−(3.6)2)(−2(1.8)+8)−{5−((1.8)−4)2−((3.6)−4)2}(−2(1.8))(−2(1.8)+8)(−2(3.6))−(−2(3.6)+8)(−2(1.8))=3.6−(16−3.24−12.96)(−3.6+8)−{5−(−2.2)2−(−0.4)2}(−3.6)(−3.6+8)(−7.2)−(−7.2+8)(−3.6)=3.5694
Now, use x1=1.8056 and y1=3.5694, the second iteration is,
x1+1=x1−u1∂v1∂y−v1∂u1∂y∂u1∂x∂v1∂y−∂u1∂y∂v1∂xx2=1.8056−{5−((1.8056)−4)2−((3.5694)−4)2}(−2(3.5694))−(16−(1.8056)2−(3.5694)2)(−2(3.5694)+8)(−2(1.8056)+8)(−2(3.5694))−(−2(3.5694)+8)(−2(1.8056))=1.8056−{−0.00081}(−7.14)−(−0.00081)(0.86)(4.389)(−7.14)−(0.86)(−3.6112)=1.80583
And,
y1+1=y1−v1∂u1∂x−u1∂v1∂x∂u1∂x∂v1∂y−∂u1∂y∂v1∂xy2=3.5694−(16−(1.8056)2−(3.5694)2)(−2(1.8056)+8)−{5−((1.8056)−4)2−((3.5694)−4)2}(−2(1.8056))(−2(1.8056)+8)(−2(3.5694))−(−2(3.5694)+8)(−2(1.8056))=3.5694−{−0.00081}(4.389)−(−0.00081)(−3.6112)(4.389)(−7.14)−(0.86)(−3.6112)=3.56917
Now, use x2=1.80583 and y2=3.56917, the third iteration is,
x2+1=x2−u2∂v2∂y−v2∂u2∂y∂u2∂x∂v2∂y−∂u2∂y∂v2∂xx3=1.80583−{5−((1.80583)−4)2−((3.56917)−4)2}(−2(3.56917))−(16−(1.80583)2−(3.56917)2)(−2(3.56917)+8)(−2(1.80583)+8)(−2(3.56917))−(−2(3.56917)+8)(−2(1.80583))=1.80583−{−0.0000035}(−7.13834)−(−0.0000035)(0.86166)(4.38834)(−7.13834)−(0.86166)(−3.61166)=1.80583
And,
y2+1=y2−v2∂u2∂x−u2∂v2∂x∂u2∂x∂v2∂y−∂u2∂y∂v2∂xy2=3.56917−(16−(1.80583)2−(3.56917)2)(−2(1.80583)+8)−{5−((1.80583)−4)2−((3.56917)−4)2}(−2(1.80583))(−2(1.80583)+8)(−2(3.56917))−(−2(3.56917)+8)(−2(1.80583))=3.56917−{−0.0000035}(4.38834)−(−0.0000035)(−3.61166)(4.38834)(−7.13834)−(0.86166)(−3.61166)=3.56917
Thus, all the iteration can be summarized as below,
| i
|
xi
|
yi
|
| 0 |
1.8 |
3.6 |
| 1 |
1.8056 |
3.5694 |
| 2 |
1.80583 |
3.56917 |
| 3 |
1.80583 |
3.56917 |
Hence, the root of the simultaneous non-linear equations y=x2+1 and y=2cosx is x=1.80583 and y=3.56917.
Use initial guesses x0=3.6 and y0=1.8, the first iteration is,
x0+1=x0−u0∂v0∂y−v0∂u0∂y∂u0∂x∂v0∂y−∂u0∂y∂v0∂xx1=3.6−{5−((3.6)−4)2−((1.8)−4)2}(−2(1.8))−(16−(3.6)2−(1.8)2)(−2(1.8)+8)(−2(3.6)+8)(−2(1.8))−(−2(1.8)+8)(−2(3.6))=3.6−{0}(−3.6)−(−0.2)(4.4)(0.8)(−3.6)−(4.4)(−7.2)=3.56944
And,
y0+1=y0−v0∂u0∂x−u0∂v0∂x∂u0∂x∂v0∂y−∂u0∂y∂v0∂xy1=1.8−(16−(3.6)2−(1.8)2)(−2(3.6)+8)−{5−((3.6)−4)2−((1.8)−4)2}(−2(3.6))(−2(3.6)+8)(−2(1.8))−(−2(1.8)+8)(−2(3.6))=1.8−{−0.2}(0.8)−(0)(−7.2)(0.8)(−3.6)−(4.4)(−7.2)=1.80556
Now, use x1=3.56944 and y1=1.80556, the second iteration is,
x1+1=x1−u1∂v1∂y−v1∂u1∂y∂u1∂x∂v1∂y−∂u1∂y∂v1∂xx2=3.56944−{5−((3.56944)−4)2−((1.80556)−4)2}(−2(1.80556))−(16−(3.56944)2−(1.80556)2)(−2(1.80556)+8)(−2(3.56944)+8)(−2(1.80556))−(−2(1.80556)+8)(−2(3.56944))=3.56944−{−0.00095}(−3.61112)−(−0.00095)(4.38888)(0.86112)(−3.61112)−(4.38888)(−7.13888)=3.56917
And,
y1+1=y1−v1∂u1∂x−u1∂v1∂x∂u1∂x∂v1∂y−∂u1∂y∂v1∂xy2=1.80556−(16−(3.56944)2−(1.80556)2)(−2(3.56944)+8)−{5−((3.56944)−4)2−((1.80556)−4)2}(−2(3.56944))(−2(3.56944)+8)(−2(1.80556))−(−2(1.80556)+8)(−2(3.56944))=1.80556−{−0.00095}(0.86112)−(−0.00095)(−7.13888)(0.86112)(−3.61112)−(4.38888)(−7.13888)=1.80583
Now, use x2=3.56917 and y2=1.80583, the third iteration is,
x2+1=x2−u2∂v2∂y−v2∂u2∂y∂u2∂x∂v2∂y−∂u2∂y∂v2∂xx3=3.56917−{5−((3.56917)−4)2−((1.80583)−4)2}(−2(1.80583))−(16−(3.56917)2−(1.80583)2)(−2(1.80583)+8)(−2(3.56917)+8)(−2(1.80583))−(−2(1.80583)+8)(−2(3.56917))=3.56917−{−0.0000035}(−3.61166)−(−0.0000035)(4.38834)(0.86166)(−3.61166)−(4.38834)(−7.13834)=3.56917
And,
y2+1=y2−v2∂u2∂x−u2∂v2∂x∂u2∂x∂v2∂y−∂u2∂y∂v2∂xy2=1.80583−(16−(3.56917)2−(1.80583)2)(−2(3.56917)+8)−{5−((3.56917)−4)2−((1.80583)−4)2}(−2(3.56917))(−2(3.56917)+8)(−2(1.80583))−(−2(1.80583)+8)(−2(3.56917))=1.80583−{−0.0000035}(0.86166)−(−0.0000035)(−7.13834)(0.86166)(−3.61166)−(4.38834)(−7.13834)=1.80583
Thus, all the iteration can be summarized as below,
| i
|
xi
|
yi
|
| 0 |
3.6 |
1.8 |
| 1 |
3.56944 |
1.80556 |
| 2 |
3.56917 |
1.80583 |
| 3 |
3.56917 |
1.80583 |
Hence, the root of the simultaneous non-linear equations y=x2+1 and y=2cosx is x=3.56917 and y=1.80583.
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
