
Concept explainers
Determine the highest real root of
(a) Graphically.
(b) Fixed-point iteration method (three iterations,
(c) Newton-Raphson method (three iterations,
(d) Secant method (three iterations,
(e) Modified secant method (three iterations,
Compute the approximate percent relative errors for your solutions.
(a)
To calculate: The highest real root of the function
Answer to Problem 2P
Solution:
The highest real root of the function
Explanation of Solution
Given:
The function,
Formula used:
The roots of the function are the points at which the graph of the function crosses the x-axis.
Calculation:
Consider the function,
Substitute different values of x and find the corresponding values of
For
For
For
For
For
Summarize the above values as shown below,
| x | |
| 0 | |
| 1 | 3 |
| 2 | |
| 3 | |
| 4 | 6.6 |
Plot the above points on the graph and join them as below,
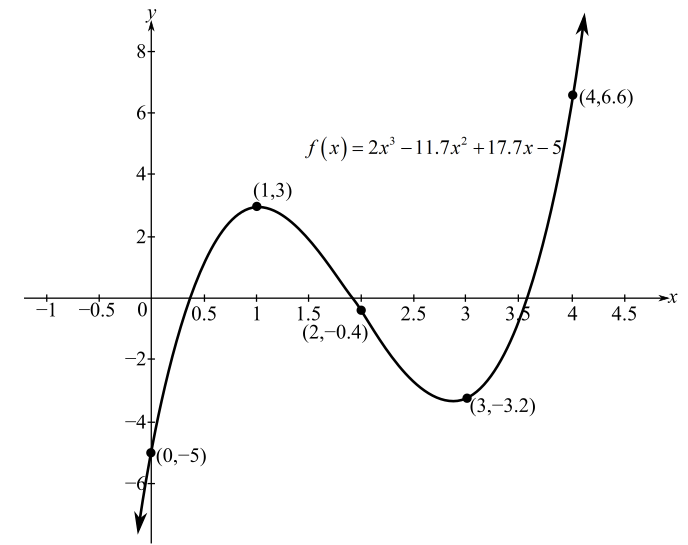
From the above graph, it is observed that the graph of the function crosses the x-axis from three points. That is, approximately
Hence, the highest real root of the function
(b)
To calculate: The highest real root of the function
Answer to Problem 2P
Solution:
The highest real root of the function
Explanation of Solution
Given:
The function,
Formula used:
The simple fixed-point iteration formula for the function
And, formula for approximate error is,
Calculation:
Consider the function,
The function can be formulated as fixed-point iteration as,
Use initial guess
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Thus, all the iteration can be summarized as below,
| 0 | 3 | |
| 1 | 3.18079 | 5.683% |
| 2 | 3.333959 | 4.594% |
| 3 | 3.4425 | 3.153% |
Hence, the highest root is 3.4425.
(c)
To calculate: The highest real root of the function
Answer to Problem 2P
Solution:
The highest real root of the function
Explanation of Solution
Given:
The function,
Formula used:
The Newton-Raphson formula,
And, formula for approximate error is,
Calculation:
Consider the function,
Differentiate the above function with respect to x,
The initial guess is
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 3 | |
| 1 | 5.133 | 41.555% |
| 2 | 4.26955 | 20.223% |
| 3 | 3.792837 | 12.569% |
Hence, the highest root is 3.792837.
(d)
To calculate: The highest real root of the function
Answer to Problem 2P
Solution:
The highest real root of the function
Explanation of Solution
Given:
The function,
Formula used:
The iterative equation of secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
The initial guess is
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Use
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 4 | |
| 1 | 3.3265 | 20.25% |
| 2 | 3.4812 | 4.443% |
| 3 | 3.58629 | 2.93% |
Hence, the highest root is 3.58629.
(e)
To calculate: The highest real root of the function
Answer to Problem 2P
Solution:
The highest real root of the function
Explanation of Solution
Given:
The function,
Formula used:
The iteration formula for modified secant method is,
And, formula for approximate error is,
Calculation:
Consider the function,
Use initial guess of
Simplify furthermore,
Therefore, the approximate error is,
Use
Simplify furthermore,
Therefore, the approximate error is,
Use
Simplify furthermore,
Therefore, the approximate error is,
Similarly, all the iteration can be summarized as below,
| 0 | 3 | |
| 1 | 4.89259 | 38.68% |
| 2 | 4.14145 | 18.14% |
| 3 | 3.7429 | 10.65% |
Hence, the highest root is 3.7429.
Want to see more full solutions like this?
Chapter 6 Solutions
Connect 1-semester Access Card For Numerical Methods For Engineers
Additional Math Textbook Solutions
Fundamentals of Differential Equations (9th Edition)
Advanced Engineering Mathematics
Basic Technical Mathematics
The Heart of Mathematics: An Invitation to Effective Thinking
High School Math 2012 Common-core Algebra 1 Practice And Problem Solvingworkbook Grade 8/9
- Find the root of e^-x ( x^2 + 5x +2) +1 = 0, using the secant method with initial guess -2 and -1 to 5dp.arrow_forwardUsing [x1 x2 x3] = [1 3 5] as the initial guess, the value of [x1 x2 x3] after three iterations in Gauss-Seidel method for:arrow_forwardSolve the approximate root of f(x) = x^5 - 3 using at least 5 iterations on Bisection Method with range from a = 0 and b = 10.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning

