
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
Chapter 7.2, Problem 39E
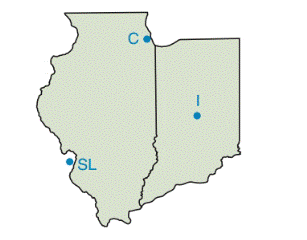
A distributing company plans an Illinois location that would be the same distance from each of its principal delivery sites at Chicago, ST. Louis, and Indianapolis. Use a construction method to locate the approximate position of the distributing company.
(Note: Trace the outline of the two states on your own paper.)
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Elementary Geometry for College Students
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 3ECh. 7.1 - In Exercises 3 to 8, use the drawing provided....Ch. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 12ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 44ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 46ECh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - What is the general name of the point of...Ch. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Which lines or line segments or rays must be drawn...Ch. 7.2 - Is it really necessary to construct all three...Ch. 7.2 - Prob. 9ECh. 7.2 - a To locate the orthocenter, is it necessary to...Ch. 7.2 - To locate the centroid of a triangle, is it...Ch. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Must the centroid of an isosceles triangle lie on...Ch. 7.2 - Draw a triangle and, by construction, find its...Ch. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Draw an obtuse triangle and, by construction, find...Ch. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Is the incenter always located in the interior of...Ch. 7.2 - Prob. 23ECh. 7.2 - Find the length of the radius of the inscribed...Ch. 7.2 - Find the distance from the circumcenter to each...Ch. 7.2 - A triangle has angles measuring 30, 30, and 120....Ch. 7.2 - Given: Isosceles RST RS=RT=17andST=16. Medians RZ,...Ch. 7.2 - Given: Isosceles RST RS=RT=10andST=16. Medians RZ,...Ch. 7.2 - In MNP, medians MB, NA and PC intersect at...Ch. 7.2 - In MNP for Exercise 29, medians MB, NA and PC...Ch. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Does a rectangle have a an incenter? b a...Ch. 7.2 - Does a square have a an incenter? b a...Ch. 7.2 - Prob. 36ECh. 7.2 - Does a rhombus have a an incenter? b a...Ch. 7.2 - Does a isosceles trapezoid have a an incenter?.b a...Ch. 7.2 - A distributing company plans an Illinois location...Ch. 7.2 - There are plans to locate a disaster response...Ch. 7.2 - A circle is inscribed in an isosceles triangle...Ch. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.3 - Describe, if possible, how you would inscribe a...Ch. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 3ECh. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 5ECh. 7.3 - In Exercises 5 to 8, perform constructions....Ch. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Find the perimeter of a regular octagon if the...Ch. 7.3 - In a regular polygon with each side of length 6.5...Ch. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Prob. 15ECh. 7.3 - Find the lengths of the side and the radius of a...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Prob. 23ECh. 7.3 - Find the measure of each exterior angle of a...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Is there a regular polygon for which each central...Ch. 7.3 - Given regular hexagon ABCDEF with each side of...Ch. 7.3 - Given regular octagon RSTUVWXY with each side of...Ch. 7.3 - Given that RSTVQ is a regular pentagon and PQR is...Ch. 7.3 - Given: Regular pentagon RSTVQ with equilateral ...Ch. 7.3 - Given: Regular pentagon JKLMN not shown with...Ch. 7.3 - Is there a regular polygon with 8 diagonals? If...Ch. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Find the measure of a central angle of a regular...Ch. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 2CRCh. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 4CRCh. 7.CR - Prob. 5CRCh. 7.CR - Prob. 6CRCh. 7.CR - Prob. 7CRCh. 7.CR - Prob. 8CRCh. 7.CR - Prob. 9CRCh. 7.CR - Prob. 10CRCh. 7.CR - Prob. 11CRCh. 7.CR - Prob. 12CRCh. 7.CR - Prob. 13CRCh. 7.CR - Prob. 14CRCh. 7.CR - Prob. 15CRCh. 7.CR - Prob. 16CRCh. 7.CR - Prob. 17CRCh. 7.CR - Prob. 18CRCh. 7.CR - Prob. 19CRCh. 7.CR - Prob. 20CRCh. 7.CR - Prob. 21CRCh. 7.CR - Prob. 22CRCh. 7.CR - Prob. 23CRCh. 7.CR - Prob. 24CRCh. 7.CR - Prob. 25CRCh. 7.CR - Prob. 26CRCh. 7.CR - Prob. 27CRCh. 7.CR - In a regular polygon, each central angle measures...Ch. 7.CR - Prob. 29CRCh. 7.CR - Prob. 30CRCh. 7.CR - Can a circle be inscribed in each of the following...Ch. 7.CR - The length of the radius of a circle inscribed in...Ch. 7.CR - Prob. 33CRCh. 7.CR - Prob. 34CRCh. 7.CT - Draw and describe the locus of points in the plane...Ch. 7.CT - Prob. 2CTCh. 7.CT - Prob. 3CTCh. 7.CT - Prob. 4CTCh. 7.CT - Describe the locus of points in space that are at...Ch. 7.CT - Prob. 6CTCh. 7.CT - For a given triangle such as ABC, what word...Ch. 7.CT - Prob. 8CTCh. 7.CT - Which of the following must be concurrent at an...Ch. 7.CT - Classify as true/false: aA circle can be inscribed...Ch. 7.CT - Prob. 11CTCh. 7.CT - Prob. 12CTCh. 7.CT - Prob. 13CTCh. 7.CT - For a regular octagon, the length of the apothem...Ch. 7.CT - For a regular hexagon ABCDEF, the length of side...Ch. 7.CT - For rectangle MNPQ, points A, B, C and D are the...Ch. 7.CT - Prob. 17CT
Additional Math Textbook Solutions
Find more solutions based on key concepts
The measure of third arc from the help of given information.
McDougal Littell Jurgensen Geometry: Student Edition Geometry
The possible names of the line containing the points.
Geometry For Enjoyment And Challenge
To identify the solid.
Geometry, Student Edition
153. A rain gutter is made from sheets of aluminum that are 20 inches wide. As shown in the figure, the edges ...
College Algebra
Use the following information to answer the next 14 exercises: The mean age for all Foothill College students f...
Introductory Statistics
Teacher Salaries
The following data from several years ago represent salaries (in dollars) from a school distri...
Elementary Statistics: A Step By Step Approach
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- There are plans to locate a disaster response agency in an area that is prone to tornadic activity. The agency is to be located at equal distances from Wichita, Tulsa and Oklahoma City. Use a construction method to locate the approximate position of the agency. Note: Trace the outline of the two states on your own paper.arrow_forwardA surveyor knows that a lot has the shape of an isosceles triangle. If the vertex angle measures 70 and each equal side is 160feet long, what measure does each of the base angles have?arrow_forwardFor coplanar points A,B, and C, suppose that you have used the Distance Formula to show that AB=5,BC=10, and AC=15. What can you conclude regarding points A,B, and C?arrow_forward
- What is the general name of the point of concurrence for the three altitudes of a triangle?arrow_forwardFor a given triangle such as ABC, what word describes the point of concurrency for athe three perpendicular bisectors of sides? bthe three altitudes?arrow_forwardWhen the bisectors of two consecutive angles of a parallelogram meet at a point on the remaining side, what type of triangle is: a DEC? b ADE? c BCE?arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell

Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Fundamental Trigonometric Identities: Reciprocal, Quotient, and Pythagorean Identities; Author: Mathispower4u;https://www.youtube.com/watch?v=OmJ5fxyXrfg;License: Standard YouTube License, CC-BY