Chapter 9, Problem 9.8P

Consider a Mach 4 airflow at a pressure of 1 atm. We wish to slow this flow to subsonic speed through a system of shock waves with as small a loss in total pressure as possible. Compare the loss in total pressure for the following three shock systems:

a. A single normal shock wave

b. An oblique shock with a deflection angle of $\text{25}.\text{3}°$, followed by a normal shock.

c. An oblique shock with a deflection angle of $\text{25}.\text{3}°$, followed by a second oblique shock of deflection angle of $\text{2}0°$, followed by a normal shock.

From the results of (a), (b), and (c), what can you induce about the efficiency of the various shock systems?

To determine

The comparison in total pressure loss for the single normal shock wave.

Answer to Problem 9.8P

The loss in pressure is $130.87\text{atm}$

Explanation of Solution

Given:

The Mach number is $M_1=4$ .

The pressure is $p_1=1\text{atm}$ .

Formula used:

The expression for $p_{0,1}$ is given as,

  $p_{0,1}=p_1{\left[1+\frac{\gamma -1}{2}{M}_1^2\right]}^{\frac{\gamma }{\gamma -1}}$

The expression for $p_{0,2}$ from normal shock table at $M_1=4$ is given as,

  $p_{0,2}=0.1388p_{0,1}$

The expression for loss in pressure is given as,

  $\text{loss}=p_{0,1}-p_{0,2}$

Calculation:

The pressure $p_{0,1}$ can be calculated as,

  $\begin{array}{l}{p}_{0,1}=p_1{\left[1+\frac{\gamma -1}{2}{M}_1^2\right]}^{\frac{\gamma }{\gamma -1}}\\ p_{0,1}=1\times {\left[1+\frac{1.4-1}{2}\times 4^2\right]}^{\frac{1.4}{1.4-1}}\\ p_{0,1}=151.83\text{atm}\end{array}$

The pressure $p_{0,2}$ can be calculated as,

  $\begin{array}{l}{p}_{0,2}=0.1388p_{0,1}\\ p_{0,2}=0.1388\times 151.83\text{atm}\\ p_{0,2}=20.953\text{atm}\end{array}$

The loss in pressure can be calculated as,

  $\begin{array}{l}\text{loss}=p_{0,1}-p_{0,2}\\ \text{loss}=151.83\text{atm}-20.953\text{atm}\\ \text{loss}=130.87\text{atm}\end{array}$

Conclusion:

Therefore, the loss in pressure is $130.87\text{atm}$ .

To determine

The comparison in pressure for an oblique shock with a deflection angle of $25.3°$ .

Answer to Problem 9.8P

The loss in pressure is $105.58\text{atm}$ .

Explanation of Solution

Given:

The Mach number is $M_1=4$ .

The pressure is $p_1=1\text{atm}$ .

The deflection angle of oblique shock wave is $\theta =25.3°$ .

Formula used:

The expression for $M_{n1}$ is given as,

  $M_{n1}=M_1\sin \beta$

The expression for $M_2$ is given as,

  $M_2=\frac{M_{n2}}{\sin \left(\beta -\theta \right)}$

The expression for $p_{0,3}$ is given as,

  $p_{0,3}=\frac{p_{0,3}}{p_{0,2}}\frac{p_{0,2}}{p_{0,1}}{p}_{0,1}$

The expression for loss in pressure is given as,

  $\text{loss}=p_{0,1}-p_{0,3}$

Calculation:

From $\theta -\beta -M$ diagram at $\theta =25.3°$ value of angle $\beta =38.5°$ .

  

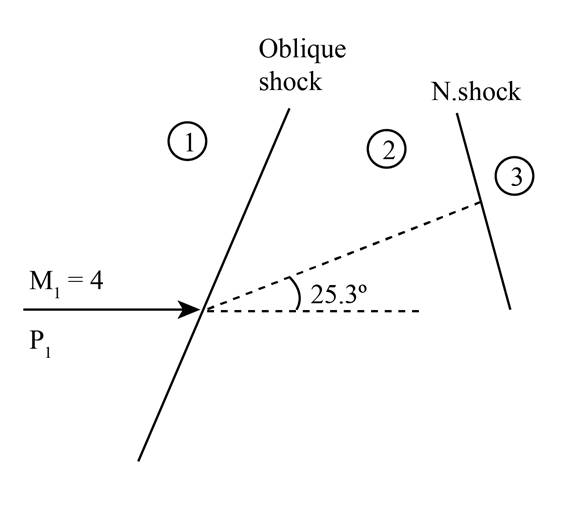
    Figure (1)

The Mach number $M_{n1}$ can be calculated as,

  $\begin{array}{l}{M}_{n1}=M_1\sin \beta \\ M_{n1}=4\times \sin \left(38.5\right)\\ M_{n1}=2.49\end{array}$

The pressure ratio for Mach number $M_{n1}=2.49$ from appendix B is given as,

  $\frac{p_{0,2}}{p_{0,1}}=0.5030$

From appendix B $M_{n2}=0.514$

The Mach number $M_2$ can be calculated as,

  $\begin{array}{l}{M}_2=\frac{M_{n2}}{\sin \left(\beta -\theta \right)}\\ M_2=\frac{0.514}{\sin \left(38.5-25.3\right)}\\ M_2=2.25\end{array}$

The pressure ratio for Mach number $M_2=2.25$ from appendix B is given as,

  $\frac{p_{0,3}}{p_{0,2}}=0.6055$

The pressure $p_{0,3}$ can be calculated as,

  $\begin{array}{l}{p}_{0,3}=\frac{p_{0,3}}{p_{0,2}}\frac{p_{0,2}}{p_{0,1}}{p}_{0,1}\\ p_{0,3}=0.5030\times 0.6055\times 151.83\text{atm}\\ p_{0,3}=46.242\text{atm}\end{array}$

The pressure loss can be calculated as,

  $\begin{array}{l}\text{loss}=p_{0,1}-p_{0,3}\\ \text{loss}=151.83\text{atm}-46.242\text{atm}\\ \text{loss}=105.58\text{}\text{atm}\end{array}$

Conclusion:

Therefore, the loss in pressure is $105.58\text{atm}$ .

To determine

The comparison in pressure for the an oblique shock with a deflection angle of $25.3°$ followed by a second oblique shock of deflection angle of $20°$ , followed by normal shock.

Answer to Problem 9.8P

The loss in pressure is $88.28\text{atm}$ .

Explanation of Solution

Given:

The Mach number is $M_1=4$ .

The pressure is $p_1=1\text{atm}$ .

The deflection angle of second oblique shock wave is $\theta =20°$ .

Formula used:

The expression for the Mach number $M_{n2}$ can be given as,

  $M_{n2}=M_2\sin {\beta }_2$

The expression for Mach number $M_3$ is given as,

  $M_3=\frac{M_{n,3}}{\sin \left({\beta }_2-\theta \right)}$

The expression for the pressure $p_{0,4}$ is given as,

  $p_{0,4}=\frac{p_{0,4}}{p_{0,3}}\frac{p_{0,3}}{p_{0,2}}\frac{p_{0,2}}{p_{0,1}}{p}_{0,1}$

The expression for loss in pressure is given as,

  $\text{loss}=p_{0,1}-p_{0,3}$

Calculation:

From $\theta -\beta -M$ diagram for $M_2=2.25$ and $\theta =20°$ the value of angle ${\beta }_2=47.3$ .

  

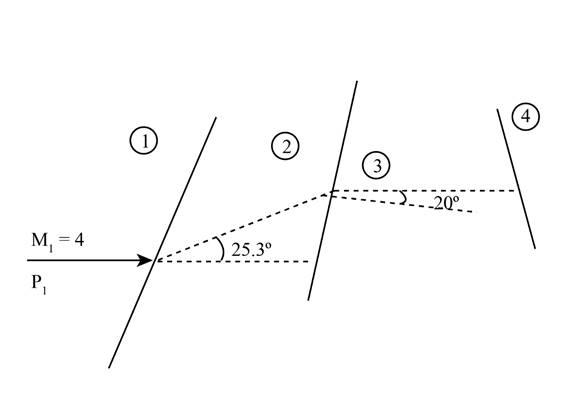
    Figure (2)

The Mach number $M_{n2}$ can be calculated as,

  $\begin{array}{l}{M}_{n2}=M_2\sin {\beta }_2\\ M_{n2}=2.25\times \sin 47.3°\\ M_{n2}=1.653\end{array}$

The pressure ratio for Mach number from appendix B is given as,

  $\frac{p_{0,3}}{p_{0,2}}=0.8740$

Refer to appendix B $M_{n3}=0.655$

The Mach number $M_3$ can be calculated as,

  $\begin{array}{l}{M}_3=\frac{M_{n,3}}{\sin \left({\beta }_2-\theta \right)}\\ M_3=\frac{0655}{\sin \left(47.3°-20°\right)}\\ M_3=1.428\end{array}$

The pressure ratio for Mach number $M_3=1.428$ from appendix B is given as,

  $\frac{p_{0,4}}{p_{0,3}}=0.9501$

The pressure $p_{0,4}$ can be calculated as,

  $\begin{array}{l}{p}_{0,4}=\frac{p_{0,4}}{p_{0,3}}\frac{p_{0,3}}{p_{0,2}}\frac{p_{0,2}}{p_{0,1}}{p}_{0,1}\\ p_{0,4}=0.9501\times 0.8740\times 0.5030\times 151.83\text{atm}\\ p_{0,4}=63.41\text{atm}\end{array}$

The pressure loss can be calculated as,

  $\begin{array}{l}\text{loss}=p_{0,1}-p_{0,4}\\ \text{loss}=151.83\text{atm}-63.41\text{atm}\\ \text{loss}=88.42\text{atm}\end{array}$

From a, b and c it is clear that the most efficient way to decrease supersonic flow to subsonic flow is through a combination of supersonic diffuser and then normal shock wave at the end.

Conclusion:

Therefore, the loss in pressure is $88.28\text{atm}$ .