
Mathematical Applications for the Management, Life, and Social Sciences
12th Edition
ISBN: 9781337625340
Author: Ronald J. Harshbarger, James J. Reynolds
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 9.3, Problem 32E
Because the derivative of a function represents both the slope of the tangent to the curve and the instantaneous rate of change of the function, it is possible to use information about one to gain information about the other. In Problems 31 and 32, use the graph of the function
given in Figure 9.26.
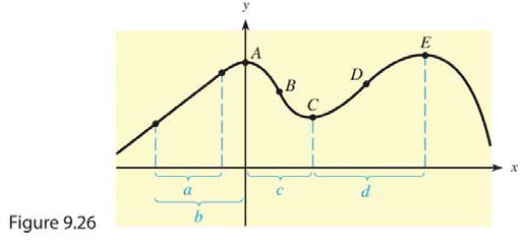
(a) At what point(s) A through E does the rate of change of f(x) change from positive to negative? (b) At what point(s) A through E does the rate of change of f(x) change from negative to positive?
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 9 Solutions
Mathematical Applications for the Management, Life, and Social Sciences
Ch. 9.1 - 1. Can exist if is undefined?
Ch. 9.1 - 2. Does exist if ?
Ch. 9.1 - 3. Does
Ch. 9.1 - 4. If , does exist?
Ch. 9.1 - 5. Let
(a) Does
(b) Find .
Ch. 9.1 - 6. Evaluate the following limits (if they...Ch. 9.1 - Prob. 7CPCh. 9.1 - Prob. 8CPCh. 9.1 - Prob. 9CPCh. 9.1 - Prob. 10CP
Ch. 9.1 - In Problems 1 -6, a graph of is shown and a...Ch. 9.1 - In Problems 1 -6, a graph of is shown and a...Ch. 9.1 - In Problems 1 -6, a graph of is shown and a...Ch. 9.1 - In Problems 1 -6, a graph of is shown and a...Ch. 9.1 - In Problems 1 -6, a graph of is shown and a...Ch. 9.1 - In Problems 1-6, a graph of y = f(x) is shown and...Ch. 9.1 - In Problems 7-10, use the graph of and the given...Ch. 9.1 - In Problems 7-10, use the graph of and the given...Ch. 9.1 - Prob. 9ECh. 9.1 - In Problems 7-10, use the graph of y = and the...Ch. 9.1 - In Problems 11-14, complete each table and predict...Ch. 9.1 - Prob. 12ECh. 9.1 - Prob. 13ECh. 9.1 - In Problems 11-14, complete each table and predict...Ch. 9.1 - Prob. 15ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 17ECh. 9.1 - Prob. 18ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 20ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 22ECh. 9.1 - Prob. 23ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 25ECh. 9.1 - Prob. 26ECh. 9.1 - Prob. 27ECh. 9.1 - Prob. 28ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 30ECh. 9.1 - Prob. 31ECh. 9.1 - Prob. 32ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 35ECh. 9.1 - In Problems 15-40, use properties of limits and...Ch. 9.1 - Prob. 37ECh. 9.1 - Prob. 38ECh. 9.1 - Prob. 39ECh. 9.1 - Prob. 40ECh. 9.1 - Prob. 41ECh. 9.1 - Prob. 42ECh. 9.1 - Prob. 43ECh. 9.1 - Prob. 44ECh. 9.1 - Prob. 45ECh. 9.1 - Prob. 46ECh. 9.1 - Prob. 47ECh. 9.1 - Prob. 48ECh. 9.1 - 49. Use values 0.1, 0.01, 0.001, 0.0001, and...Ch. 9.1 - 50. (a) If if it exists. Explain your...Ch. 9.1 - Prob. 51ECh. 9.1 - 52. If and find
(a)
(b)
(c)
(d)
Ch. 9.1 - Prob. 53ECh. 9.1 - Prob. 54ECh. 9.1 - 55. Revenue The total revenue for a product is...Ch. 9.1 - 56. Profit If the profit function for a product is...Ch. 9.1 - Prob. 57ECh. 9.1 - 58. Sales and training During the first 4 months...Ch. 9.1 - 59. Advertising and sales Suppose that the daily...Ch. 9.1 - Prob. 60ECh. 9.1 - 61. Productivity During an 8-hour shift, the rate...Ch. 9.1 - Prob. 62ECh. 9.1 - 63. Cost-benefit Suppose that the cost C of...Ch. 9.1 - 64. Cost-benefit Suppose that the cost C of...Ch. 9.1 - 65. Federal income tax The following table shows...Ch. 9.1 - Prob. 66ECh. 9.1 - Prob. 67ECh. 9.1 - 68. Airport parking The Hourly Parking Garage at...Ch. 9.1 - Dow Jones Industrial Average The graph in the...Ch. 9.1 - Dow Jones Industrial Average The graph in the...Ch. 9.1 - Prob. 71ECh. 9.1 - Prob. 72ECh. 9.2 - 1. Find any x-values where the following functions...Ch. 9.2 - Prob. 2CPCh. 9.2 - Prob. 3CPCh. 9.2 - In Problems 1 and 2, refer to the figure. For each...Ch. 9.2 - In Problems 1 and 2, refer to the figure. For each...Ch. 9.2 - In Problems 3-8, determine whether each function...Ch. 9.2 - In Problems 3-8, determine whether each function...Ch. 9.2 - In Problems 3-8, determine whether each function...Ch. 9.2 - In Problems 3-8, determine whether each function...Ch. 9.2 - In Problems 3-8, determine whether each function...Ch. 9.2 - In Problems 3-8, determine whether each function...Ch. 9.2 - Prob. 9ECh. 9.2 - Prob. 10ECh. 9.2 - In Problems 9-16, determine whether the given...Ch. 9.2 - Prob. 12ECh. 9.2 - In Problems 9-16, determine whether the given...Ch. 9.2 - Prob. 14ECh. 9.2 - Prob. 15ECh. 9.2 - In Problems 9-16, determine whether the given...Ch. 9.2 - Prob. 17ECh. 9.2 - Prob. 18ECh. 9.2 - Prob. 19ECh. 9.2 - Prob. 20ECh. 9.2 -
Each of Problems 21-24 contains a function and...Ch. 9.2 - Each of Problems 21-24 contains a function and its...Ch. 9.2 - Prob. 23ECh. 9.2 - Prob. 24ECh. 9.2 - Prob. 25ECh. 9.2 - Prob. 26ECh. 9.2 - Prob. 27ECh. 9.2 - Prob. 28ECh. 9.2 - Prob. 29ECh. 9.2 - Prob. 30ECh. 9.2 - Prob. 31ECh. 9.2 - Prob. 32ECh. 9.2 - Prob. 33ECh. 9.2 - Prob. 34ECh. 9.2 - Prob. 35ECh. 9.2 - In Problems 35 and 36, complete (a)-(c). Use...Ch. 9.2 - Prob. 37ECh. 9.2 - For Problems 37 and 38, let
be a rational...Ch. 9.2 - 39. Sales volume Suppose that the weekly sales...Ch. 9.2 - 40. Worker productivity Suppose that the average...Ch. 9.2 - 41. Demand Suppose that the demand for a product...Ch. 9.2 - 42. Advertising and sales The sales volume y (in...Ch. 9.2 - 43. Annuities If an annuity can make an unending...Ch. 9.2 - 44. Response to adrenalin Experimental evidence...Ch. 9.2 - 45. Cost-benefit Suppose that the cost C of...Ch. 9.2 - 46. Pollution Suppose that the cost C of removing...Ch. 9.2 - 47. Pollution The percent p of particulate...Ch. 9.2 - Prob. 48ECh. 9.2 - Prob. 49ECh. 9.2 - 50. Calories and temperature Suppose that the...Ch. 9.2 - Prob. 52ECh. 9.3 - 1. Find the average rate of change of over [1,...Ch. 9.3 - 2. For the function , find each of the...Ch. 9.3 - 3. Which of the following are given by ?
(a) The...Ch. 9.3 - 4. Must a graph that has no discontinuity, corner,...Ch. 9.3 - In Problems 1-4, for each given function, find the...Ch. 9.3 - In Problems 1-4, for each given function, find the...Ch. 9.3 - In Problems 1-4, for each given function, find the...Ch. 9.3 - In Problems 1-4, for each given function, find the...Ch. 9.3 - 5. Given , find the average rate of change of f(x)...Ch. 9.3 - 6. Given , find the average rate of change of f(x)...Ch. 9.3 - Prob. 7ECh. 9.3 - 8. In Example 6 in this section, we were given
....Ch. 9.3 - 9. Let .
(a) Use the definition of derivative and...Ch. 9.3 - 10. Let .
(a) Use the definition of derivative and...Ch. 9.3 - In Problems 11-14, the tangent line to the graph...Ch. 9.3 - Prob. 12ECh. 9.3 - In Problems 11-14, the tangent line to the graph...Ch. 9.3 - Prob. 14ECh. 9.3 - For each function in Problems 15-18, find
(a) the...Ch. 9.3 - For each function in Problems 15-18, find
(a) the...Ch. 9.3 - Prob. 17ECh. 9.3 - Prob. 18ECh. 9.3 - For each function in Problems 19-22, approximate...Ch. 9.3 - Prob. 20ECh. 9.3 - Prob. 21ECh. 9.3 - For each function in Problems 19-22, approximate...Ch. 9.3 - Prob. 23ECh. 9.3 - Prob. 24ECh. 9.3 - In the figures given in Problems 25 and 26, at...Ch. 9.3 - Prob. 26ECh. 9.3 - Prob. 27ECh. 9.3 - Prob. 28ECh. 9.3 - Prob. 29ECh. 9.3 - 30. If the instantaneous rate of change of g(x) at...Ch. 9.3 - Because the derivative of a function represents...Ch. 9.3 - Because the derivative of a function represents...Ch. 9.3 - 33. Given the graph of ) in Figure 9.27, determine...Ch. 9.3 - Prob. 34ECh. 9.3 - Prob. 35ECh. 9.3 - Prob. 36ECh. 9.3 - Prob. 37ECh. 9.3 - In Problems 35-38, (a) find the slope of the...Ch. 9.3 - 39. Total cost Suppose total cost in dollars from...Ch. 9.3 - 40. Average velocity If an object is thrown upward...Ch. 9.3 - 41. Demand If the demand for a product is given...Ch. 9.3 - 42. Revenue If the total revenue function for a...Ch. 9.3 - Prob. 43ECh. 9.3 - 44. b The figure shows the percent of the U.S....Ch. 9.3 - 45. Marginal revenue The revenue function for a...Ch. 9.3 - 46. Marginal revenue Suppose the total revenue...Ch. 9.3 - 47. Labor force and output The monthly output at...Ch. 9.3 - 48. Consumer expenditure Suppose that the demand...Ch. 9.3 - 49. Profit Suppose that the profit function for...Ch. 9.3 - 50. Profit It the total revenue function and the...Ch. 9.3 - 51. Heat index The highest recorded temperature in...Ch. 9.3 - 52. Receptivity In learning theory, receptivity is...Ch. 9.3 - Prob. 53ECh. 9.3 - Prob. 54ECh. 9.4 - 1. True or false: The derivative of a constant...Ch. 9.4 - 2. True or false: The derivative of the sum of two...Ch. 9.4 - 3. True or false: The derivative of the difference...Ch. 9.4 - 4. Does the Coefficient Rule apply to , where c is...Ch. 9.4 - Prob. 5CPCh. 9.4 - Prob. 6CPCh. 9.4 - Find the derivatives of the functions in Problems...Ch. 9.4 - Prob. 2ECh. 9.4 - Prob. 3ECh. 9.4 - Prob. 4ECh. 9.4 - Prob. 5ECh. 9.4 - Prob. 6ECh. 9.4 - Prob. 7ECh. 9.4 - Prob. 8ECh. 9.4 - Find the derivatives of the functions in Problems...Ch. 9.4 - Prob. 10ECh. 9.4 - Prob. 11ECh. 9.4 - Prob. 12ECh. 9.4 - Find the derivatives of the functions in Problems...Ch. 9.4 - Find the derivatives of the functions in Problems...Ch. 9.4 - In Problems 15-18, at the indicated points,...Ch. 9.4 - Prob. 16ECh. 9.4 - In Problems 15-18, at the indicated points,...Ch. 9.4 - Prob. 18ECh. 9.4 - In Problems 19-26, find the derivative of each...Ch. 9.4 - In Problems 19-26, find the derivative of each...Ch. 9.4 - In Problems 19-26, find the derivative of each...Ch. 9.4 - Prob. 22ECh. 9.4 - Prob. 23ECh. 9.4 - In Problems 19-26, find the derivative of each...Ch. 9.4 - In Problems 19-26, find the derivative of each...Ch. 9.4 - In Problems 19-26, find the derivative of each...Ch. 9.4 - In Problems 27-30, write the equation of the...Ch. 9.4 - In Problems 27-30, write the equation of the...Ch. 9.4 - In Problems 27-30, write the equation of the...Ch. 9.4 - In Problems 27-30, write the equation of the...Ch. 9.4 - In Problems 31-34, find the coordinates of points...Ch. 9.4 - Prob. 32ECh. 9.4 - In Problems 31-34, find the coordinates of points...Ch. 9.4 - Prob. 34ECh. 9.4 - Prob. 35ECh. 9.4 - Prob. 36ECh. 9.4 - Prob. 37ECh. 9.4 - Prob. 38ECh. 9.4 - Prob. 39ECh. 9.4 - Prob. 40ECh. 9.4 - Prob. 41ECh. 9.4 - Prob. 42ECh. 9.4 - Prob. 43ECh. 9.4 - Prob. 44ECh. 9.4 - Prob. 45ECh. 9.4 - For each function in Problems 43-46, do the...Ch. 9.4 - Prob. 47ECh. 9.4 - 48. Revenue The total revenue, in dollars, for a...Ch. 9.4 - Prob. 49ECh. 9.4 - 50. Capital investment and output The monthly...Ch. 9.4 - 51. Demand The demand for q units of a product...Ch. 9.4 - Prob. 52ECh. 9.4 - 53. Cost and average cost Suppose that the total...Ch. 9.4 - 54. Cost and average cost Suppose that the total...Ch. 9.4 - 55. Cost-benefit Suppose that tor a certain city,...Ch. 9.4 - Prob. 56ECh. 9.4 - 57. Wind chill One form of the formula that...Ch. 9.4 - Prob. 58ECh. 9.5 - 1. True or false: The derivative of the product of...Ch. 9.5 - 2. True or false: The derivative of the quotient...Ch. 9.5 - Prob. 3CPCh. 9.5 - Prob. 4CPCh. 9.5 - 5. If , where c is a constant, does finding y'...Ch. 9.5 - Prob. 1ECh. 9.5 - In Problems 1-4, find the derivative and...Ch. 9.5 - Prob. 3ECh. 9.5 - In Problems 1-4, find the derivative and...Ch. 9.5 - In Problems 5-8, find the derivative but do not...Ch. 9.5 - In Problems 5-8, find the derivative but do not...Ch. 9.5 - In Problems 5-8, find the derivative but do not...Ch. 9.5 - In Problems 5-8, find the derivative but do not...Ch. 9.5 - In Problems 9 and 10, at each indicated point,...Ch. 9.5 - In Problems 9 and 10, at each indicated point,...Ch. 9.5 - In Problems 11-20, find the indicated derivatives...Ch. 9.5 - In Problems 11-20, find the indicated derivatives...Ch. 9.5 - In Problems 11-20, find the indicated derivatives...Ch. 9.5 - Prob. 14ECh. 9.5 - Prob. 15ECh. 9.5 - Prob. 16ECh. 9.5 - In Problems 11-20, find the indicated derivatives...Ch. 9.5 - Prob. 18ECh. 9.5 - Prob. 19ECh. 9.5 - Prob. 20ECh. 9.5 - In Problems 21 and 22, at the indicated point for...Ch. 9.5 - In Problems 21 and 22, at the indicated point for...Ch. 9.5 - In Problems 23-26, write the equation of the...Ch. 9.5 - In Problems 23-26, write the equation of the...Ch. 9.5 - Prob. 25ECh. 9.5 - Prob. 26ECh. 9.5 - Prob. 27ECh. 9.5 - Prob. 28ECh. 9.5 - Prob. 29ECh. 9.5 - Prob. 30ECh. 9.5 - Prob. 35ECh. 9.5 - Prob. 36ECh. 9.5 - Prob. 37ECh. 9.5 - 38. Use the Quotient Rule to show that the Powers...Ch. 9.5 - Prob. 39ECh. 9.5 - 40. Cost-benefit If the cost C (in dollars) of...Ch. 9.5 - 41. Revenue Suppose the revenue (in dollars) from...Ch. 9.5 - 42. Revenue The revenue (in dollars) from the sale...Ch. 9.5 - Prob. 43ECh. 9.5 - Prob. 44ECh. 9.5 - 45. Response to a drug The reaction R to an...Ch. 9.5 - 46. Nerve response The number of action potentials...Ch. 9.5 - 47. Test reliability If a test having reliability...Ch. 9.5 - 48. Advertising and sales The sales of a product s...Ch. 9.5 - 49. Candidate recognition Suppose that the...Ch. 9.5 - Prob. 50ECh. 9.5 - 51. Wind chill Each winter the so-called “polar...Ch. 9.5 - 52. Response to injected adrenalin Experimental...Ch. 9.5 - Prob. 53ECh. 9.5 - 54. Emissions The table shows data for sulfur...Ch. 9.5 - Prob. 55ECh. 9.5 - Prob. 56ECh. 9.6 -
Ch. 9.6 - 2. (a) If , find f'(x) by using the Power Rule...Ch. 9.6 - Prob. 1ECh. 9.6 - Prob. 2ECh. 9.6 - Differentiate the functions in Problems 3-20.
3.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
4.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
5.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
6.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
7.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
8.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
9.
Ch. 9.6 - Differentiate the functions in Problems 3-20.
10....Ch. 9.6 - Differentiate the functions in Problems 3-20.
11....Ch. 9.6 - Differentiate the functions in Problems 3-20.
12....Ch. 9.6 - Differentiate the functions in Problems 3-20.
13....Ch. 9.6 - Differentiate the functions in Problems 3-20.
14....Ch. 9.6 - Differentiate the functions in Problems 3-20.
15....Ch. 9.6 - Differentiate the functions in Problems 3-20.
16....Ch. 9.6 - Differentiate the functions in Problems 3-20.
17....Ch. 9.6 - Differentiate the functions in Problems 3-20.
18....Ch. 9.6 - Differentiate the functions in Problems 3-20.
19....Ch. 9.6 - Differentiate the functions in Problems 3-20.
20....Ch. 9.6 - At the indicated point, for each function in...Ch. 9.6 - At the indicated point, for each function in...Ch. 9.6 - At the indicated point, for each function in...Ch. 9.6 - At the indicated point, for each function in...Ch. 9.6 - In Problems 25-28, write the equation of the line...Ch. 9.6 - In Problems 25-28, write the equation of the line...Ch. 9.6 - In Problems 25-28, write the equation of the line...Ch. 9.6 - In Problems 25-28, write the equation of the line...Ch. 9.6 - In Problems 29 and 30, complete the following for...Ch. 9.6 - In Problems 29 and 30, complete the following for...Ch. 9.6 - In Problems 31 and 32, do the following for each...Ch. 9.6 - In Problems 31 and 32, do the following for each...Ch. 9.6 - In Problems 33 and 34, find the derivative of each...Ch. 9.6 - In Problems 33 and 34, find the derivative of each...Ch. 9.6 - 35. Ballistics Ballistics experts are able to...Ch. 9.6 - 36. Population of microorganisms Suppose that the...Ch. 9.6 - 37. Revenue The revenue from the sale of a product...Ch. 9.6 - Prob. 38ECh. 9.6 - 39. Pricing and sales Suppose that the weekly...Ch. 9.6 - 40. Pricing and sales A chain of auto service...Ch. 9.6 - 41. Demand Suppose that the demand tor q units of...Ch. 9.6 - Prob. 42ECh. 9.6 - Stimulus-response The relation between the...Ch. 9.6 - Prob. 44ECh. 9.6 - 45. Demand If the demand for q units of a product...Ch. 9.6 - 46. Advertising and sales The daily sales S (in...Ch. 9.6 - Prob. 47ECh. 9.6 - 48. Data entry speed The data entry speed (in...Ch. 9.6 - 49. Investments If an IRA is a variable-rate...Ch. 9.6 - Prob. 50ECh. 9.6 - Prob. 51ECh. 9.6 - 52. Energy use Energy use per dollar of GDP...Ch. 9.6 - 53. Gross domestic product The table shows U.S....Ch. 9.6 - Prob. 54ECh. 9.7 - 1. If a function has the form , where n is a...Ch. 9.7 - Prob. 2CPCh. 9.7 - Prob. 3CPCh. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Prob. 12ECh. 9.7 - Prob. 13ECh. 9.7 - Prob. 14ECh. 9.7 - Prob. 15ECh. 9.7 - Prob. 16ECh. 9.7 - Prob. 17ECh. 9.7 - Prob. 18ECh. 9.7 - Prob. 19ECh. 9.7 - Prob. 20ECh. 9.7 - Prob. 21ECh. 9.7 - Prob. 22ECh. 9.7 - Prob. 23ECh. 9.7 - Prob. 24ECh. 9.7 - Prob. 25ECh. 9.7 - Find the derivatives of the functions in Problems...Ch. 9.7 - Prob. 27ECh. 9.7 - Prob. 28ECh. 9.7 - Prob. 29ECh. 9.7 - Prob. 30ECh. 9.7 - Prob. 31ECh. 9.7 - Prob. 32ECh. 9.7 - In Problems 33 and 34, find the derivative of each...Ch. 9.7 - Prob. 34ECh. 9.7 - Prob. 35ECh. 9.7 - 36. Revenue Suppose that the revenue function for...Ch. 9.7 - 37. Revenue Suppose that the revenue in dollars...Ch. 9.7 - Prob. 38ECh. 9.7 - Prob. 39ECh. 9.7 - 40. Demand Suppose that the demand function for q...Ch. 9.7 - Prob. 41ECh. 9.7 - 42. Advertising and sales Suppose that sales (in...Ch. 9.7 - 43. Advertising and sales An inferior product with...Ch. 9.7 - 44. Advertising and sales An excellent film with a...Ch. 9.7 - 45. Per capita expenditures for U.S. health care...Ch. 9.8 - Suppose that the distance a particle travels is...Ch. 9.8 - Prob. 2CPCh. 9.8 - Prob. 3CPCh. 9.8 - Prob. 4CPCh. 9.8 - Prob. 1ECh. 9.8 - Prob. 2ECh. 9.8 - In Problems 1-6, find the second derivative.
Ch. 9.8 - Prob. 4ECh. 9.8 - Prob. 5ECh. 9.8 - Prob. 6ECh. 9.8 - In Problems 7-12, find the third derivative.
Ch. 9.8 - In Problems 7-12, find the third derivative.
Ch. 9.8 - In Problems 7-12, find the third derivative.
Ch. 9.8 - In Problems 7-12, find the third derivative.
Ch. 9.8 - In Problems 7-12, find the third derivative.
Ch. 9.8 - In Problems 7-12, find the third derivative.
Ch. 9.8 - In Problems 13-24, find the indicated...Ch. 9.8 - In Problems 13-24, find the indicated...Ch. 9.8 - Prob. 15ECh. 9.8 - Prob. 16ECh. 9.8 - In Problems 13-24, find the indicated...Ch. 9.8 - Prob. 18ECh. 9.8 - In Problems 13-24, find the indicated...Ch. 9.8 - Prob. 20ECh. 9.8 - Prob. 21ECh. 9.8 - Prob. 22ECh. 9.8 - Prob. 23ECh. 9.8 - Prob. 24ECh. 9.8 - Prob. 25ECh. 9.8 - Prob. 26ECh. 9.8 - In Problems 27-30, use the numerical derivative...Ch. 9.8 - Prob. 28ECh. 9.8 - Prob. 29ECh. 9.8 - Prob. 30ECh. 9.8 - Prob. 31ECh. 9.8 - Prob. 32ECh. 9.8 - 33. Acceleration A particle travels as a function...Ch. 9.8 - 34. Acceleration If the formula describing the...Ch. 9.8 - 35. Revenue The revenue (in dollars) from the sale...Ch. 9.8 - 36. Revenue Suppose that the revenue (in dollars)...Ch. 9.8 - 37. Sensitivity When medicine is administered,...Ch. 9.8 - 38. Photosynthesis The amount of photosynthesis...Ch. 9.8 - 39. Revenue The revenue (in thousands of dollars)...Ch. 9.8 - Prob. 40ECh. 9.8 - 41. Advertising and sales The daily sales S (in...Ch. 9.8 - 42. Advertising and sales A product with a large...Ch. 9.8 - Prob. 43ECh. 9.8 - Prob. 44ECh. 9.8 - Prob. 47ECh. 9.9 - Suppose the total cost function for a commodity is...Ch. 9.9 - Suppose the total cost function for a commodity is...Ch. 9.9 - Suppose the total cost function for a commodity is...Ch. 9.9 - Suppose the total cost function for a commodity is...Ch. 9.9 - Suppose the total cost function for a commodity is...Ch. 9.9 - Prob. 6CPCh. 9.9 - If the total profit function for a product is ,...Ch. 9.9 - In Problems 1-8, total revenue is in dollars and x...Ch. 9.9 - In Problems 1-8, total revenue is in dollars and x...Ch. 9.9 - In Problems 1-8, total revenue is in dollars and x...Ch. 9.9 - In Problems 1-8, total revenue is in dollars and x...Ch. 9.9 - In Problems 1-8, total revenue is in dollars and x...Ch. 9.9 - In Problems 1-8, total revenue is in dollars and x...Ch. 9.9 - Prob. 7ECh. 9.9 - Prob. 8ECh. 9.9 - Prob. 9ECh. 9.9 - Prob. 10ECh. 9.9 - In Problems 9-16, cost is in dollars and x is the...Ch. 9.9 - Prob. 12ECh. 9.9 - Prob. 13ECh. 9.9 - Prob. 14ECh. 9.9 - In Problems 9-16, cost is in dollars and x is the...Ch. 9.9 - Prob. 16ECh. 9.9 - Prob. 17ECh. 9.9 - Prob. 18ECh. 9.9 - 19. If the cost function for a commodity is
...Ch. 9.9 - Prob. 20ECh. 9.9 - Prob. 21ECh. 9.9 - Prob. 22ECh. 9.9 - In each of Problems 23 and 24, the graph of a...Ch. 9.9 - Prob. 24ECh. 9.9 - Prob. 25ECh. 9.9 - Prob. 26ECh. 9.9 - In Problems 25-28, cost, revenue, and profit are...Ch. 9.9 - In Problems 25-28, cost, revenue, and profit are...Ch. 9.9 - In each of Problems 29 and 30, the graphs of a...Ch. 9.9 - In each of Problems 29 and 30, the graphs of a...Ch. 9.9 - Prob. 31ECh. 9.9 - Prob. 32ECh. 9.9 - Prob. 33ECh. 9.9 - Prob. 34ECh. 9.9 - 35. The price of a product in a competitive market...Ch. 9.9 - 36. The cost per unit of producing a product is ...Ch. 9.9 - 37. If the daily cost per unit of producing a...Ch. 9.9 - 38. The Mary Ellen Candy Company produces...Ch. 9 - In Problems 1-6, use the graph of in Figure 9.40...Ch. 9 - In Problems 1-6, use the graph of in Figure 9.40...Ch. 9 - Prob. 3RECh. 9 - Prob. 4RECh. 9 - In Problems 1-6, use the graph of in Figure 9.40...Ch. 9 - Prob. 6RECh. 9 - Prob. 7RECh. 9 - Prob. 8RECh. 9 - Prob. 9RECh. 9 - Prob. 10RECh. 9 - In Problems 7-20, find each limit, if it exists.
Ch. 9 - Prob. 12RECh. 9 - Prob. 13RECh. 9 - In Problems 7-20, find each limit, if it exists.
Ch. 9 - Prob. 15RECh. 9 - Prob. 16RECh. 9 - Prob. 17RECh. 9 - Prob. 18RECh. 9 - Prob. 19RECh. 9 - Prob. 20RECh. 9 - Prob. 21RECh. 9 - Prob. 22RECh. 9 - Use the graph of y = f(x) in Figure 9.40 to answer...Ch. 9 - Prob. 24RECh. 9 - Prob. 25RECh. 9 - Prob. 26RECh. 9 - Prob. 27RECh. 9 - Prob. 28RECh. 9 - Prob. 29RECh. 9 - Prob. 30RECh. 9 - Prob. 31RECh. 9 - Prob. 32RECh. 9 - Prob. 33RECh. 9 - Prob. 34RECh. 9 - Prob. 35RECh. 9 - Prob. 36RECh. 9 - Prob. 37RECh. 9 - Prob. 38RECh. 9 - Prob. 39RECh. 9 - Prob. 40RECh. 9 - In Problems 40 and 41, decide whether the...Ch. 9 - Prob. 42RECh. 9 - Prob. 43RECh. 9 - Prob. 44RECh. 9 - Prob. 45RECh. 9 - Prob. 46RECh. 9 - Prob. 47RECh. 9 - Prob. 48RECh. 9 - Prob. 49RECh. 9 - Prob. 50RECh. 9 - 51. If
Ch. 9 - Prob. 52RECh. 9 - Prob. 53RECh. 9 - Prob. 54RECh. 9 - Prob. 55RECh. 9 - 56. If
Ch. 9 - Prob. 57RECh. 9 - Prob. 58RECh. 9 - Prob. 59RECh. 9 - 60. Write the equation of the line tangent to the...Ch. 9 - Prob. 61RECh. 9 - Prob. 62RECh. 9 - 63. If
Ch. 9 -
Ch. 9 - Prob. 65RECh. 9 - Prob. 66RECh. 9 - Prob. 67RECh. 9 - Prob. 68RECh. 9 -
Ch. 9 - Prob. 70RECh. 9 - Prob. 71RECh. 9 - Prob. 72RECh. 9 - Prob. 73RECh. 9 - Prob. 74RECh. 9 - Prob. 75RECh. 9 - Prob. 76RECh. 9 - Prob. 77RECh. 9 - Prob. 78RECh. 9 - Prob. 79RECh. 9 - Prob. 80RECh. 9 - Prob. 81RECh. 9 - Prob. 82RECh. 9 - Prob. 83RECh. 9 - Prob. 84RECh. 9 - Prob. 85RECh. 9 - Prob. 86RECh. 9 - Prob. 87RECh. 9 - Prob. 88RECh. 9 - Prob. 89RECh. 9 - Prob. 90RECh. 9 - Prob. 91RECh. 9 - Prob. 92RECh. 9 - Prob. 93RECh. 9 - Prob. 94RECh. 9 - Prob. 95RECh. 9 - Prob. 96RECh. 9 - Prob. 97RECh. 9 - Prob. 98RECh. 9 - Prob. 99RECh. 9 - In Problems 100-107, cost, revenue, and profit are...Ch. 9 - Prob. 101RECh. 9 -
In Problems 100-107, cost, revenue, and profit...Ch. 9 - Prob. 103RECh. 9 - Prob. 104RECh. 9 - Prob. 105RECh. 9 - Prob. 106RECh. 9 - Prob. 107RECh. 9 - Prob. 108RECh. 9 - Prob. 1TCh. 9 - Prob. 2TCh. 9 - Prob. 3TCh. 9 - Prob. 4TCh. 9 - Prob. 5TCh. 9 - Prob. 6TCh. 9 - Prob. 7TCh. 9 - Prob. 8TCh. 9 - Prob. 9TCh. 9 - Prob. 10TCh. 9 - Prob. 11TCh. 9 - Prob. 12TCh. 9 - Prob. 13TCh. 9 - Prob. 14TCh. 9 - Prob. 15TCh. 9 - Prob. 16TCh. 9 - Prob. 18TCh. 9 - Prob. 19TCh. 9 - Prob. 20TCh. 9 - Prob. 21TCh. 9 - Prob. 22TCh. 9 - Prob. 23T
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Recommended textbooks for you
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education

Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education

Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON


Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON

Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,

Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Derivatives of Trigonometric Functions - Product Rule Quotient & Chain Rule - Calculus Tutorial; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=_niP0JaOgHY;License: Standard YouTube License, CC-BY