
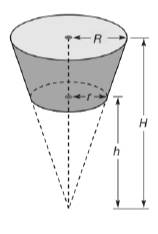
A frustum of a cone is the portion of the cone bounded between the circular base and a plane parallel to the base. With dimensions are indicated, show that the volume of the frustum of the cone is
 |
Want to see the full answer?
Check out a sample textbook solution
Chapter 9 Solutions
Elementary Geometry for College Students
Additional Math Textbook Solutions
Geometry, Student Edition
McDougal Littell Jurgensen Geometry: Student Edition Geometry
Geometry For Enjoyment And Challenge
Finite Mathematics with Applications In the Management, Natural, and Social Sciences (12th Edition)
Introduction to Statistical Quality Control
Elementary and Intermediate Algebra: Concepts and Applications (7th Edition)
- Find the exact volume of the solid that results when the region bounded in quadrant I by the axes and the lines x=9 and y=5 revolved about the a x-axis b y-axisarrow_forwardFind the volume of the oblique circular cylinder. The axis meets the plane of the base to form a 45 angle.arrow_forwardFind the exact lateral area of each solid in Exercise 40. Find the exact volume of the solid formed when the region bounded in Quadrant I by the axes and the lines x = 9 and y = 5 is revolved about the a) x-axis b) y-axisarrow_forward
- For the right triangular prism found in Exercise 16, suppose that the sides of the triangular base measures 3 ft, 4 ft, and 5 ft. The altitude is 6 ft in length. a Find the lateral area of the prism. b Find the total area of the prism. c Find the volume area of the prism.arrow_forwardFind the exact volume of the solid that results when the rectangular region with vertices at 0, 0, 6, 0, 6, 4 and 0, 4 is revolved about the a x-axis b y-axisarrow_forwardFor the right triangular prism, suppose that the sides of the triangular base measure 4 m, 5 m, and 6 m. The altitude is 7 m. a Find the lateral area of the prism. b Find the total area of the prism. c Find the volume of the prism.arrow_forward
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage, Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning



