
Edit the given Python Code (about Probability) so it can also output two Bar Graphs. Please see the attached pics to complete it.
Code that Needs to be Edited:
from collections import Counter
from scipy.stats import binom
# Part A: Find the 7 most common repetitive numbers
number_list = [25, 23, 17, 25, 48, 34, 29, 34, 38, 42, 30, 50, 58, 36, 39, 28, 27, 35, 30, 34, 46, 46, 39, 51, 46, 75,
66, 20, 45, 28, 35, 41, 43, 56, 37, 38, 50, 52, 33, 44, 37, 72, 47, 20, 80, 52, 38, 44, 39, 49, 50, 56,
62, 42, 54, 59, 35, 35, 32, 31, 37, 43, 48, 47, 38, 71, 56, 53, 51, 25, 36, 54, 47, 71, 53, 59, 41, 42,
57, 50, 38, 31, 27, 33, 26, 40, 42, 31, 25, 26, 47, 26, 37, 42, 15, 60, 40, 43, 48, 30, 25, 52, 28, 41,
40, 34, 28, 40, 38, 40, 30, 35, 27, 27, 32, 44, 31, 32, 29, 31, 25, 21, 23, 25, 39, 33, 21, 36, 21, 14,
23, 33, 27, 31, 16, 23, 21, 13, 20, 40, 13, 27, 33, 34, 31, 13, 40, 58, 24, 24, 17, 18, 18, 21, 18, 16,
24, 15, 18, 33, 21, 13, 24, 21, 29, 31, 26, 18, 23, 22, 21, 32, 33, 24, 30, 30, 21, 23, 29, 23, 25, 18,
10, 20, 13, 18, 28, 12, 17, 18, 20, 15, 16, 16, 25, 21, 18, 26, 17, 22, 16, 15, 15, 25, 14, 18, 19, 16,
14, 20, 28, 13, 28, 39, 40, 29, 25, 27, 26, 18, 17, 20, 25, 25, 22, 19, 14, 21, 22, 18, 10, 29, 24, 21,
21, 13, 15, 25, 20, 29, 22, 11, 14, 17, 17, 13, 21, 11, 19, 17, 18, 20, 8, 21, 18, 24, 21, 15, 27, 21]
number_count = Counter(number_list)
most_common = number_count.most_common(7)
print("Most Common Numbers in New Testament:")
for num, count in most_common:
print(f"Number {num} appears {count} times")
# Part B: Find the 7 most uncommon numbers
least_common = number_count.most_common()[:-8:-1]
print("\nLeast Common Numbers in New Testament:")
for num, count in least_common:
print(f"Number {num} appears {count} times")
# Part C: Use binomial distribution to find the probability of each of the 7 common repetitive numbers
print("\nProbabilities of 7 Most Common Numbers (Using Binomial Distribution):")
for num, count in most_common:
total_trials = len(number_list)
successes = count
probability = binom.pmf(successes, total_trials, successes/total_trials)
print(f"Probability of seeing {num} appear exactly {count} times: {probability:.4f}")
print("\nProbabilities of 7 Most Common Numbers from the New Testament Winning the Powerball:")
# The provided "how often" data from the table
how_often_data = {
1: 4, 2: 4, 3: 3, 4: 7, 5: 8, 6: 4, 7: 3, 8: 4, 9: 6, 10: 3,
11: 2, 12: 3, 13: 3, 14: 5, 15: 2, 16: 5, 17: 2, 18: 4, 19: 3,
20: 4, 21: 8, 22: 1, 23: 5, 24: 1, 25: 2, 26: 4
}
# The total count of all occurrences
total_count = sum(how_often_data.values())
# The specific numbers we need to find the probabilities for
requested_numbers = [17, 18, 20, 21, 25, 27, 31]
# Calculate the probabilities
probabilities = {number: how_often_data.get(number, 0) / total_count for number in requested_numbers}
def print_probability(number, probability):
if number in how_often_data:
print(f"Probability of Number {number} being a winning number for Powerball: {probability:.4f}")
else:
print(f"Probability of Number {number} being a winning number is 0 because it is not a Powerball number.")
for number in requested_numbers:
print_probability(number, probabilities[number])
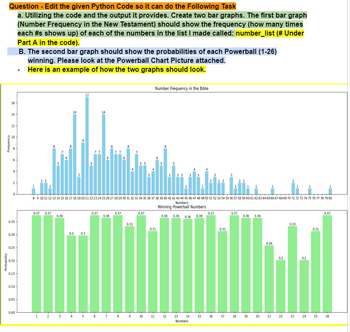
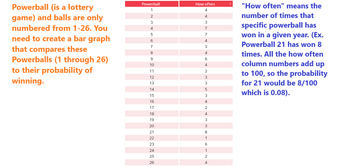
Step by stepSolved in 2 steps with 2 images

 EBK JAVA PROGRAMMINGComputer ScienceISBN:9781337671385Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK JAVA PROGRAMMINGComputer ScienceISBN:9781337671385Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage Learning EBK JAVA PROGRAMMINGComputer ScienceISBN:9781305480537Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT
EBK JAVA PROGRAMMINGComputer ScienceISBN:9781305480537Author:FARRELLPublisher:CENGAGE LEARNING - CONSIGNMENT- Np Ms Office 365/Excel 2016 I NtermedComputer ScienceISBN:9781337508841Author:CareyPublisher:Cengage
 Microsoft Visual C#Computer ScienceISBN:9781337102100Author:Joyce, Farrell.Publisher:Cengage Learning,
Microsoft Visual C#Computer ScienceISBN:9781337102100Author:Joyce, Farrell.Publisher:Cengage Learning, Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning





