Steel Design (Activate Learning with these NEW titles from Engineering!)
6th Edition
ISBN: 9781337094740
Author: Segui, William T.
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 1, Problem 1.5.6P
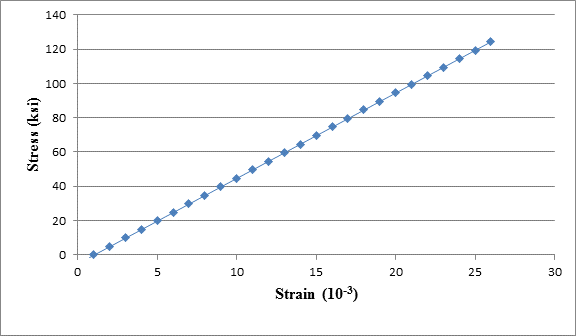
The data in Table 1.5.3 were obtained from a tensile test of a metal specimen with a rectangular cross section of
a. Generate a table of stress and strain values.
b. Plot these values and draw a best-fit line to obtain a stress-strain curve.
c. Determine the modulus of elasticity from the slope of the linear portion of the curve.
d. Estimate the value of the proportional limit.
e. Use the
Expert Solution & Answer
Trending nowThis is a popular solution!
Students have asked these similar questions
During a tension test, measurements for the applied load and the corresponding elongation are taken at frequent intervals. These data points are then used to:
a. calculate the stress caused by the applied load at each data point.
b. calculate the strain in the specimen induced by the applied load at each data point.
c. plot a stress-strain diagram.
d. all of the above
1.5-6
The data shown in the table were obtained from a tensile test of a metal specimen with
a diameter of 0.500 inch and a gage length (the length over which the elongation is
measured) of 2.00 inches. The specimen was not loaded to failure.
a. Generate a table of stress and strain values.
b. Plot these values and draw a best-fit line to obtain a stress-strain curve.
c. Use the slope of the best-fit line to estimate the modulus of elasticity.
Load (kips)
PI223 SIN
0
2.5
3.5
10
11.5
12
Elongation (in.)
0
0.0010
0.0014
0.0020
0.0024
0.0036
0.0044
0.0050
0.0060
0.0070
0.0080
0.0120
0.0180
1.5-7
The data shown in the table were obtained from a tensile test of a metal specimen with
a rectangular cross section of 0.2 in.² in area and a gage length (the length over which
the elongation is measured) of 2.000 inches.
a. Generate a table of stress and strain values.
b. Plot these values and draw a best-fit line to obtain a stress-strain curve.
c. Determine the modulus of elasticity from the slope of the linear portion of the curve.
Load
(kips)
0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
5.5
50
6.0
6.5
Elongation × 10³
(in.)
0
0.160
0.352
0.706
1.012
1.434
1.712
1.986
2.286
2.612
2.938
3.274
3.632
3.976
Load
(kips)
7.0
7.5
8.0
8.5
9.0
9.5
10.0
10.5
11.0
11.5
12.0
12.5
13
Elongation × 10³
(in.)
4.386
4.640
4.988
5.432
5.862
6.362
7.304
8.072
9.044
11.310
14.120
20.044
29.106
Chapter 1 Solutions
Steel Design (Activate Learning with these NEW titles from Engineering!)
Ch. 1 - Prob. 1.5.1PCh. 1 - A tensile test was performed on a metal specimen...Ch. 1 - A tensile test was performed on a metal specimen...Ch. 1 - A tensile test was performed on a metal specimen...Ch. 1 - The results of a tensile test are shown in Table...Ch. 1 - The data in Table 1.5.3 were obtained from a...
Additional Engineering Textbook Solutions
Find more solutions based on key concepts
11-1. Determine the moments at A,B, and C, then draw
the moment diagram for the beam. The moment of ine...
Structural Analysis (10th Edition)
5.11 What error results on a 200-ft sight with a level if the rod reading is 6.307 ft but the top of the
7-ft r...
Elementary Surveying: An Introduction To Geomatics (15th Edition)
A 3 ft square footing carries a sustained load of 10 k. It is placed on the surface of a 30 ft thick saturated ...
Foundation Design: Principles and Practices (3rd Edition)
1.2 Explain the difference between geodetic and plane
surveys,
Elementary Surveying (14th Edition)
What production method for steel shapes is specified by the following organizations? AISI (American Iron and St...
Structural Steel Design (6th Edition)
State three examples of a static load application and three examples of a dynamic load application.
Materials for Civil and Construction Engineers (4th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, civil-engineering and related others by exploring similar questions and additional content below.Similar questions
- The data shown in the table were obtained from a tensile test of a metal specimen with a rectangular cross-section of 0.2 in.? in area and a gage length (the length over which the elongation is measured) of 2.000 inches. a. Generate a table of stress and strain values. b. Plot these values and draw a best-fit line to obtain a stress-strain curve. c. Determine the modulus of elasticity from the slope of the linear portion of the curve. d. Estimate the value of the proportional limit. e. Use the 0.2% offset method to determine the yield stress.arrow_forwardThe tensile test was conducted on a specimen with a diameter of 0.5 inch. A strain gage was bonded to the specimen so that the strain could be obtained directly. The following data were obtained. a) create a table of stress and strain values. Plot this data points and draw the best fit straight line through them. b) what is the slope of this line? What does this value represent?arrow_forwardsniparrow_forward
- 1.5-7 The data shown in the table were obtained from a tensile test of a metal specimen with a rectangular cross section of 0.2 in.² in area and a gage length (the length over which the elongation is measured) of 2.000 inches. d. Estimate the value of the proportional limit. e. Use the 0.2% offset method to determine the yield stress. Load (kips) 0 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0 4.5 5.0 ܩܙ ܘ 5.5 6.0 6.5 Elongation × 10³ (in.) 0 0.160 0.352 0.706 1.012 1.434 1.712 1.986 2.286 2.612 2.938 3.274 3.632 3.976 Load (kips) 7.0 7.5 8.0 8.5 9.0 9.5 10.0 10.5 11.0 11.5 12.0 12.5 13 Elongation × 10³ (in.) 4.386 4.640 4.988 5.432 5.862 6.362 7.304 8.072 9.044 11.310 14.120 20.044 29.106arrow_forwardThe (G-E) diagram obtained in the tensile test performed on a metal sample with a diameter of 16 mm is as follows. The loads at points A, B and C and the elongation measured on l. 16 cm gauge length were determined as follows: B A B C Load (kgf) 4800 8400 7200 Elongation (mm) 0.192 28.8 38.4 c) Calculate the fracture work and the maximum elastic energy the metal rod can store. d) Find the cross-sectional area of a 6 m long rod made of this metal such that it can carry 12 tons of load with 2 times the safety of yield strength. How long does the rod extend under this load?arrow_forwardAn aluminium specimen with an initial gauge diameter d, = 10 mm and gauge length, 1, = 100 mm is %3D subjected to tension test. A tensile force P= 50 kN is applied at the ends of the specimen as shown, resulting in an elongation of 1 mm in gauge length. The Poisson's ratio (µ) of the specimen is Take shear modulus of material, G = 25 GPa. Consider engineering stress-strain conditions. Parrow_forward
- a. Calculate the ductility of the sample as a percentage (%) b. Calculate the stress required to create a neck in the sample, in MPa.arrow_forwardShow steps, final answer is suppose to be -1.877x10^6 Nmmarrow_forwardIn a standard tensile test, an aluminum rod of 20-mm diameter is subjected to a tension force of P = 30 kN. Knowing that E = 70 GPa, and the change in diameter of the rod= 0.00955 mm, determine the poissons' ratio v. -20-mm diameter gage length=150 mmarrow_forward
- 1.16 The stress-strain relationship shown in Figure P1.16 was obtained during the tensile test of an aluminum alloy specimen. 60,000 H Stress, psi 40,000 20,000 0 Figure P1.16 0.002 0.004 0.006 0.008 Strain, in./in. Determine the following: a. Young's modulus within the linear portion. b. Tangent modulus at a stress of 45,000 psi c. Yield stress using an offset of 0.002 strain d. If the yield stress in part c is considered failure stress, what is the maximum working stress to be applied to this material if a factor of safety of 1.5 is used? 4arrow_forwardThe results of a tensile test are shown in Table 1.5.2. The test was performed on a metal specimen with a circular cross section. The diameter was 3⁄8 inch and the gage length (the length over which the elongation is measured) was 2 inches. a. Use the data in Table 1.5.2 to produce a table of stress and strain values. b. Plot the stress–strain data and draw a best-fit curve. c. Compute the modulus of elasticity from the initial slope of the curve. d. Estimate the yield stressarrow_forward2.31 A uniaxial test was performed on a bone specimen having a central (gauge) region initially 6 mm long and 2 mm in diameter. Five data points were recorded: Axial force (N) 94 190 284 376 440 Change in length (mm) 0.009 0.018 0.027 0.050 0.094 Plot the associated stress-strain relation, calculate a Young's modulus, and show that the yield stress is ~118 MPa. Recall that the yield stress reveals the transition from elastic to plastic (cf. Fig. 2.25). Data from Özkaya and Nordin (1999).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Steel Design (Activate Learning with these NEW ti...Civil EngineeringISBN:9781337094740Author:Segui, William T.Publisher:Cengage Learning
Materials Science And Engineering PropertiesCivil EngineeringISBN:9781111988609Author:Charles GilmorePublisher:Cengage Learning
Steel Design (Activate Learning with these NEW ti...
Civil Engineering
ISBN:9781337094740
Author:Segui, William T.
Publisher:Cengage Learning
Materials Science And Engineering Properties
Civil Engineering
ISBN:9781111988609
Author:Charles Gilmore
Publisher:Cengage Learning
Material Properties 101; Author: Real Engineering;https://www.youtube.com/watch?v=BHZALtqAjeM;License: Standard YouTube License, CC-BY