
Multivariable Calculus
8th Edition
ISBN: 9781305266643
Author: James Stewart
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Textbook Question
Chapter 10, Problem 57RE
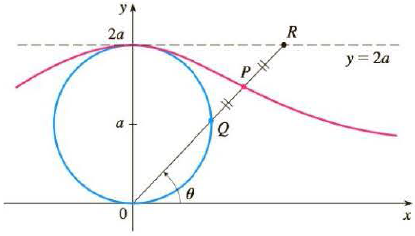
In the figure the circle of radius a is stationary, and for every θ, the point P is the midpoint of the segment QR. The curve traced out by P for 0 < θ < π is called the long-bow curve. Find parametric equations for this curve.
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 10 Solutions
Multivariable Calculus
Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Prob. 3ECh. 10.1 - Prob. 4ECh. 10.1 - Prob. 5ECh. 10.1 - Prob. 6ECh. 10.1 - Prob. 7ECh. 10.1 - Prob. 8ECh. 10.1 - Prob. 9ECh. 10.1 - Prob. 10E
Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Prob. 14ECh. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Prob. 16ECh. 10.1 - Prob. 17ECh. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Suppose a curve is given by the parametric...Ch. 10.1 - Prob. 24ECh. 10.1 - Prob. 25ECh. 10.1 - Prob. 26ECh. 10.1 - Prob. 27ECh. 10.1 - Match the parametric equations with the graphs...Ch. 10.1 - Graph the curve x = y 2 sin y.Ch. 10.1 - Graph the curves y = x3 4x and x = y3 4y and...Ch. 10.1 - (a) Show that the parametric equations...Ch. 10.1 - Use a graphing device and the result of Exercise...Ch. 10.1 - Find parametric equations for the path of a...Ch. 10.1 - (a) Find parametric equations for the ellipse...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Compare the curves represented by the parametric...Ch. 10.1 - Prob. 38ECh. 10.1 - Derive Equations 1 for the case /2 .Ch. 10.1 - Let P be a point at a distance d from the center...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - Prob. 43ECh. 10.1 - (a) Find parametric equations for the set of all...Ch. 10.1 - Suppose that the position of one particle at time...Ch. 10.1 - Prob. 46ECh. 10.1 - Investigate the family of curves defined by the...Ch. 10.1 - Prob. 48ECh. 10.1 - Prob. 49ECh. 10.1 - Graph several members of the family of curves x =...Ch. 10.1 - The curves with equations x = a sin nt, y = b cos...Ch. 10.1 - Prob. 52ECh. 10.2 - Find dy/dx. 1. x=t1+t,y=1+tCh. 10.2 - Find dy/dx. 2. x = tet, y = t + sin tCh. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Prob. 8ECh. 10.2 - Prob. 9ECh. 10.2 - Prob. 10ECh. 10.2 - Prob. 11ECh. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Prob. 14ECh. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Prob. 18ECh. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Prob. 20ECh. 10.2 - Prob. 21ECh. 10.2 - Use a graph to estimate the coordinates of the...Ch. 10.2 - Prob. 23ECh. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Prob. 25ECh. 10.2 - Graph the curve x = 2 cos t, y = sin t + sin 2t to...Ch. 10.2 - (a) Find the slope of the tangent line to the...Ch. 10.2 - (a) Find the slope of the tangent to the astroid x...Ch. 10.2 - At what point(s) on the curve x = 3t2 + 1, y = t3 ...Ch. 10.2 - Find equations of the tangents to the curve x =...Ch. 10.2 - Use the parametric equations of an ellipse, x = a...Ch. 10.2 - Find the area enclosed by the curve x = t2 2t,...Ch. 10.2 - Find the area enclosed by the x-axis and the curve...Ch. 10.2 - Find the area of the region enclosed by the...Ch. 10.2 - Find the area under one arch of the trochoid of...Ch. 10.2 - Let R be the region enclosed by the loop of the...Ch. 10.2 - Prob. 37ECh. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Prob. 39ECh. 10.2 - Prob. 40ECh. 10.2 - Find the exact length of the curve. 41. x = 1 +...Ch. 10.2 - Find the exact length of the curve. 42. x = et t,...Ch. 10.2 - Prob. 43ECh. 10.2 - Prob. 44ECh. 10.2 - Prob. 45ECh. 10.2 - Prob. 46ECh. 10.2 - Prob. 47ECh. 10.2 - Find the length of the loop of the curve x = 3t ...Ch. 10.2 - Use Simpsons Rule with n = 6 to estimate the...Ch. 10.2 - In Exercise 10.1.43 you were asked to derive the...Ch. 10.2 - Find the distance traveled by a particle with...Ch. 10.2 - Find the distance traveled by a particle with...Ch. 10.2 - Prob. 53ECh. 10.2 - Find the total length of the astroid x = a cos3, y...Ch. 10.2 - (a) Graph the epitrochoid with equations...Ch. 10.2 - Prob. 57ECh. 10.2 - Prob. 58ECh. 10.2 - Prob. 59ECh. 10.2 - Prob. 60ECh. 10.2 - Prob. 61ECh. 10.2 - Prob. 62ECh. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Prob. 64ECh. 10.2 - Find the surface area generated by rotating the...Ch. 10.2 - Find the surface area generated by rotating the...Ch. 10.2 - If f is continuous and f(t) 0 for a t b, show...Ch. 10.2 - Prob. 68ECh. 10.2 - The curvature at a point P of a curve is defined...Ch. 10.2 - (a) Use the formula in Exercise 69(b) to find the...Ch. 10.2 - Use the formula in Exercise 69(a) to find the...Ch. 10.2 - (a) Show that the curvature at each point of a...Ch. 10.2 - A string is wound around a circle and then unwound...Ch. 10.2 - A cow is tied to a silo with radius r by a rope...Ch. 10.3 - Prob. 1ECh. 10.3 - Prob. 2ECh. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Prob. 5ECh. 10.3 - Prob. 6ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 8ECh. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Prob. 10ECh. 10.3 - Prob. 11ECh. 10.3 - Prob. 12ECh. 10.3 - Prob. 13ECh. 10.3 - Prob. 14ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 16ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 18ECh. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Prob. 20ECh. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Prob. 22ECh. 10.3 - Prob. 23ECh. 10.3 - Prob. 24ECh. 10.3 - Prob. 25ECh. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Prob. 27ECh. 10.3 - Prob. 28ECh. 10.3 - Prob. 29ECh. 10.3 - Prob. 30ECh. 10.3 - Prob. 31ECh. 10.3 - Prob. 32ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 34ECh. 10.3 - Prob. 35ECh. 10.3 - Prob. 36ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 40ECh. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Prob. 42ECh. 10.3 - Prob. 43ECh. 10.3 - Prob. 44ECh. 10.3 - Prob. 45ECh. 10.3 - Prob. 46ECh. 10.3 - Prob. 47ECh. 10.3 - Prob. 48ECh. 10.3 - Prob. 49ECh. 10.3 - Prob. 50ECh. 10.3 - Show that the curve r = sin tan (called a...Ch. 10.3 - Prob. 52ECh. 10.3 - (a) In Example 11 the graphs suggest that the...Ch. 10.3 - Prob. 54ECh. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Prob. 60ECh. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Prob. 63ECh. 10.3 - Prob. 64ECh. 10.3 - Prob. 65ECh. 10.3 - Prob. 66ECh. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Prob. 68ECh. 10.3 - Prob. 69ECh. 10.3 - Prob. 70ECh. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Prob. 72ECh. 10.3 - Prob. 73ECh. 10.3 - Use a graph to estimate the y-coordinate of the...Ch. 10.3 - Prob. 75ECh. 10.3 - Prob. 76ECh. 10.3 - Let P be any point (except the origin) on the...Ch. 10.3 - Prob. 78ECh. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Prob. 4ECh. 10.4 - Find the area of the shaded region. 5.Ch. 10.4 - Find the area of the shaded region. 6.Ch. 10.4 - Prob. 7ECh. 10.4 - Prob. 8ECh. 10.4 - Prob. 9ECh. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Prob. 11ECh. 10.4 - Prob. 12ECh. 10.4 - Prob. 13ECh. 10.4 - Prob. 14ECh. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Prob. 16ECh. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Prob. 18ECh. 10.4 - Prob. 19ECh. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Prob. 21ECh. 10.4 - Prob. 22ECh. 10.4 - Prob. 23ECh. 10.4 - Prob. 24ECh. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Prob. 28ECh. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Prob. 30ECh. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Prob. 32ECh. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Prob. 34ECh. 10.4 - Find the area inside the larger loop and outside...Ch. 10.4 - Prob. 36ECh. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Prob. 38ECh. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Prob. 40ECh. 10.4 - Prob. 41ECh. 10.4 - Prob. 42ECh. 10.4 - The points of intersection of the cardioid r = 1 +...Ch. 10.4 - When recording live performances, sound engineers...Ch. 10.4 - Prob. 45ECh. 10.4 - Prob. 46ECh. 10.4 - Find the exact length of the polar curve. 47. r =...Ch. 10.4 - Prob. 48ECh. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Prob. 50ECh. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - Prob. 52ECh. 10.4 - Prob. 53ECh. 10.4 - Prob. 54ECh. 10.4 - Prob. 55ECh. 10.4 - Prob. 56ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Prob. 2ECh. 10.5 - Prob. 3ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Prob. 5ECh. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Prob. 8ECh. 10.5 - Prob. 9ECh. 10.5 - Prob. 10ECh. 10.5 - Prob. 11ECh. 10.5 - Prob. 12ECh. 10.5 - Prob. 13ECh. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Prob. 15ECh. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Prob. 17ECh. 10.5 - Prob. 18ECh. 10.5 - Prob. 19ECh. 10.5 - Prob. 20ECh. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Prob. 22ECh. 10.5 - Prob. 23ECh. 10.5 - Prob. 24ECh. 10.5 - Prob. 25ECh. 10.5 - Prob. 26ECh. 10.5 - Prob. 27ECh. 10.5 - Prob. 28ECh. 10.5 - Prob. 29ECh. 10.5 - Prob. 30ECh. 10.5 - Prob. 31ECh. 10.5 - Prob. 32ECh. 10.5 - Prob. 33ECh. 10.5 - Prob. 34ECh. 10.5 - Prob. 35ECh. 10.5 - Prob. 36ECh. 10.5 - Prob. 37ECh. 10.5 - Prob. 38ECh. 10.5 - Prob. 39ECh. 10.5 - Prob. 40ECh. 10.5 - Prob. 41ECh. 10.5 - Prob. 42ECh. 10.5 - Prob. 43ECh. 10.5 - Prob. 44ECh. 10.5 - Prob. 45ECh. 10.5 - Prob. 46ECh. 10.5 - Prob. 47ECh. 10.5 - Prob. 48ECh. 10.5 - Prob. 49ECh. 10.5 - A cross-section of a parabolic reflector is shown...Ch. 10.5 - Prob. 51ECh. 10.5 - Prob. 52ECh. 10.5 - Prob. 53ECh. 10.5 - Prob. 54ECh. 10.5 - Determine the type of curve represented by the...Ch. 10.5 - (a) Show that the equation of the tangent line to...Ch. 10.5 - Prob. 57ECh. 10.5 - Show that if an ellipse and a hyperbola have the...Ch. 10.5 - Use parametric equations and Simpsons Rule with n...Ch. 10.5 - Prob. 60ECh. 10.5 - Prob. 61ECh. 10.5 - Prob. 62ECh. 10.5 - Find the centroid of the region enclosed by the...Ch. 10.5 - (a) Calculate the surface area of the ellipsoid...Ch. 10.5 - Let P(x1, y1) be a point on the ellipse x2/a2 +...Ch. 10.5 - Prob. 66ECh. 10.6 - Prob. 1ECh. 10.6 - Prob. 2ECh. 10.6 - Prob. 3ECh. 10.6 - Prob. 4ECh. 10.6 - Prob. 5ECh. 10.6 - Prob. 6ECh. 10.6 - Prob. 7ECh. 10.6 - Prob. 8ECh. 10.6 - Prob. 9ECh. 10.6 - Prob. 10ECh. 10.6 - Prob. 11ECh. 10.6 - Prob. 12ECh. 10.6 - Prob. 13ECh. 10.6 - Prob. 14ECh. 10.6 - Prob. 15ECh. 10.6 - Prob. 16ECh. 10.6 - Prob. 17ECh. 10.6 - Prob. 18ECh. 10.6 - Prob. 19ECh. 10.6 - Prob. 20ECh. 10.6 - Prob. 21ECh. 10.6 - Prob. 22ECh. 10.6 - Prob. 23ECh. 10.6 - Prob. 24ECh. 10.6 - Prob. 25ECh. 10.6 - Prob. 26ECh. 10.6 - Prob. 27ECh. 10.6 - Prob. 28ECh. 10.6 - Prob. 29ECh. 10.6 - Prob. 30ECh. 10.6 - Prob. 31ECh. 10 - (a) What is a parametric curve? (b) How do you...Ch. 10 - (a) How do you find the slope of a tangent to a...Ch. 10 - Prob. 3RCCCh. 10 - (a) Use a diagram to explain the meaning of the...Ch. 10 - Prob. 5RCCCh. 10 - Prob. 6RCCCh. 10 - Prob. 7RCCCh. 10 - Prob. 8RCCCh. 10 - Prob. 9RCCCh. 10 - Prob. 1RQCh. 10 - Prob. 2RQCh. 10 - Prob. 3RQCh. 10 - Prob. 4RQCh. 10 - Prob. 5RQCh. 10 - Prob. 6RQCh. 10 - Prob. 7RQCh. 10 - Prob. 8RQCh. 10 - Prob. 9RQCh. 10 - Prob. 10RQCh. 10 - Prob. 1RECh. 10 - Prob. 2RECh. 10 - Prob. 3RECh. 10 - Prob. 4RECh. 10 - Prob. 5RECh. 10 - Prob. 6RECh. 10 - Prob. 7RECh. 10 - Prob. 8RECh. 10 - Prob. 9RECh. 10 - Prob. 10RECh. 10 - Prob. 11RECh. 10 - Prob. 12RECh. 10 - Prob. 13RECh. 10 - Sketch the polar curve. 14. r = 2 cos(/2)Ch. 10 - Prob. 15RECh. 10 - Prob. 16RECh. 10 - Prob. 17RECh. 10 - Prob. 18RECh. 10 - Prob. 19RECh. 10 - Prob. 20RECh. 10 - Find the slope of the tangent line to the given...Ch. 10 - Find the slope of the tangent line to the given...Ch. 10 - Prob. 23RECh. 10 - Prob. 24RECh. 10 - Prob. 25RECh. 10 - Find dy/dx and d2y/dx2. 26. x = 1 + t2, y = t t3Ch. 10 - Prob. 27RECh. 10 - Prob. 28RECh. 10 - Prob. 29RECh. 10 - Prob. 30RECh. 10 - Prob. 31RECh. 10 - Find the area enclosed by the inner loop of the...Ch. 10 - Find the points of intersection of the curves r =...Ch. 10 - Prob. 34RECh. 10 - Find the area of the region that lies inside both...Ch. 10 - Find the area of the region that lies inside the...Ch. 10 - Prob. 37RECh. 10 - Prob. 38RECh. 10 - Prob. 39RECh. 10 - Prob. 40RECh. 10 - Prob. 41RECh. 10 - Prob. 42RECh. 10 - Prob. 43RECh. 10 - Prob. 44RECh. 10 - Prob. 45RECh. 10 - Prob. 46RECh. 10 - Prob. 47RECh. 10 - Prob. 48RECh. 10 - Prob. 49RECh. 10 - Prob. 50RECh. 10 - Find an equation of the hyperbola with foci (0, 4)...Ch. 10 - Find an equation of the ellipse with foci (3, 2)...Ch. 10 - Prob. 53RECh. 10 - Prob. 54RECh. 10 - Prob. 55RECh. 10 - Prob. 56RECh. 10 - In the figure the circle of radius a is...Ch. 10 - A curve called the folium of Descartes is defined...Ch. 10 - Prob. 1PCh. 10 - (a) Find the highest and lowest points on the...Ch. 10 - Prob. 3PCh. 10 - Four bugs are placed at the four comers of a...Ch. 10 - Show that any tangent line to a hyperbola touches...Ch. 10 - A circle C of radius 2r has its center at the...
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Sketch the curve represented by each set of equations by eliminating the parameter. a. x=5cos and y=3sin,02 b. x=1+tan and y=2+2sec,/23/2arrow_forwardLongbow CurveIn the following figure, the circle of radius a is stationary, and for every , the point P is the midpoint of the segment QR. The curve traced out by P for 0<< is called the longbow curve. Find the parametric equations for this curve.arrow_forward
Recommended textbooks for you
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Implicit Differentiation Explained - Product Rule, Quotient & Chain Rule - Calculus; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=LGY-DjFsALc;License: Standard YouTube License, CC-BY