Math
CalculusMultivariable CalculusLet P ( x 1 , y 1 ) be a point on the ellipse x 2 / a 2 + y 2 / b 2 = 1 with foci F 1 and F 2 and let α and β be the angles between the lines PF 1 , PF 2 and the ellipse as shown in the figure. Prove that α = β . This explains how whispering galleries and lithotripsy work. Sound coming from one focus is reflected and passes through the other focus. [ Hint: Use the formula in Problem 17 on page 201 to show that tan α = tan β .]

Let P ( x 1 , y 1 ) be a point on the ellipse x 2 / a 2 + y 2 / b 2 = 1 with foci F 1 and F 2 and let α and β be the angles between the lines PF 1 , PF 2 and the ellipse as shown in the figure. Prove that α = β . This explains how whispering galleries and lithotripsy work. Sound coming from one focus is reflected and passes through the other focus. [ Hint: Use the formula in Problem 17 on page 201 to show that tan α = tan β .]

BuyFind

Multivariable Calculus

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781305266643
BuyFind

Multivariable Calculus

8th Edition
James Stewart
Publisher: Cengage Learning
ISBN: 9781305266643

Solutions

Chapter
Section
Problem 1E
Problem 2E
Problem 3E
Problem 4E
Problem 5E
Problem 6E
Problem 7E
Problem 8E
Problem 9E
Problem 10E
Problem 11E
Problem 12E
Problem 13E
Problem 14E
Problem 15E
Problem 16E
Problem 17E
Problem 18E
Problem 19E
Problem 20E
Problem 21E
Problem 22E
Problem 23E
Problem 24E
Problem 25E
Problem 26E
Problem 27E
Problem 28E
Problem 29E
Problem 30E
Problem 31E
Problem 32E
Problem 33E
Problem 34E
Problem 35E
Problem 36E
Problem 37E
Problem 38E
Problem 39E
Problem 40E
Problem 41E
Problem 42E
Problem 43E
Problem 44E
Problem 45E
Problem 46E
Problem 47E
Problem 48E
Problem 49E
Problem 50E
Problem 51E
Problem 52E
Problem 53E
Problem 54E
Problem 55E
Problem 56E
Problem 57E
Problem 58E
Problem 59E
Problem 60E
Problem 61E
Problem 62E
Problem 63E
Problem 64E
Problem 65E
Problem 66E
Chapter 10.5, Problem 65E
Textbook Problem

Let P(x1, y1) be a point on the ellipse x2/a2 + y2/b2 = 1 with foci F1 and F2 and let α and β be the angles between the lines PF1, PF2 and the ellipse as shown in the figure. Prove that α = β. This explains how whispering galleries and lithotripsy work. Sound coming from one focus is reflected and passes through the other focus. [Hint: Use the formula in Problem 17 on page 201 to show that tan α = tan β.]

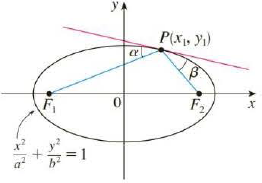
Chapter 10.5, Problem 65E, Let P(x1, y1) be a point on the ellipse x2/a2 + y2/b2 = 1 with foci F1 and F2 and let and be the

Expert Solution

Want to see the full answer?

Check out a sample textbook solution.
Chapter 10.5,
Problem 64E
Chapter 10.5,
Problem 66E

Want to see this answer and more?

Experts are waiting 24/7 to provide step-by-step solutions in as fast as 30 minutes!*

*Response times vary by subject and question complexity. Median response time is 34 minutes and may be longer for new subjects.

Chapter 10 Solutions

Multivariable Calculus
Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - Sketch the curve by using the parametric equations...Ch. 10.1 - (a) Sketch the curve by using the parametric...Ch. 10.1 - (a) Sketch the curve by using the parametric...Ch. 10.1 - (a) Sketch the curve by using the parametric...Ch. 10.1 - (a) Sketch the curve by using the parametric...Ch. 10.1 - (a) Sketch the curve by using the parametric...Ch. 10.1 - (a) Sketch the curve by using the parametric...
Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - (a) Eliminate the parameter to find a Cartesian...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Describe the motion of a particle with position...Ch. 10.1 - Suppose a curve is given by the parametric...Ch. 10.1 - Match the graphs of the parametric equations x =...Ch. 10.1 - Use the graphs of x = f(t) and y = g(t) to sketch...Ch. 10.1 - Use the graphs of x = f(t) and y = g(t) to sketch...Ch. 10.1 - Use the graphs of x = f(t) and y = g(t) to sketch...Ch. 10.1 - Match the parametric equations with the graphs...Ch. 10.1 - Graph the curve x = y 2 sin y.Ch. 10.1 - Graph the curves y = x3 4x and x = y3 4y and...Ch. 10.1 - (a) Show that the parametric equations...Ch. 10.1 - Use a graphing device and the result of Exercise...Ch. 10.1 - Find parametric equations for the path of a...Ch. 10.1 - (a) Find parametric equations for the ellipse...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Use a graphing calculator or computer to reproduce...Ch. 10.1 - Compare the curves represented by the parametric...Ch. 10.1 - Compare the curves represented by the parametric...Ch. 10.1 - Derive Equations 1 for the case /2 .Ch. 10.1 - Let P be a point at a distance d from the center...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - If a and b are fixed numbers, find parametric...Ch. 10.1 - A curve, called a witch of Maria Agnesi, consists...Ch. 10.1 - (a) Find parametric equations for the set of all...Ch. 10.1 - Suppose that the position of one particle at time...Ch. 10.1 - If a projectile is fired with an initial velocity...Ch. 10.1 - Investigate the family of curves defined by the...Ch. 10.1 - The swallowtail catastrophe curves ate defined by...Ch. 10.1 - Graph several members of the family of curves with...Ch. 10.1 - Graph several members of the family of curves x =...Ch. 10.1 - The curves with equations x = a sin nt, y = b cos...Ch. 10.1 - Investigate the family of curves defined by the...Ch. 10.2 - Find dy/dx. 1. x=t1+t,y=1+tCh. 10.2 - Find dy/dx. 2. x = tet, y = t + sin tCh. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find an equation of the tangent to the curve at...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find dy/dx and d2y/dx2. For which values of t is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Find the points on the curve where the tangent is...Ch. 10.2 - Use a graph to estimate the coordinates of the...Ch. 10.2 - Use a graph to estimate the coordinates of the...Ch. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Graph the curve in a viewing rectangle that...Ch. 10.2 - Show that the curve x = cos t, y = sin t cos t has...Ch. 10.2 - Graph the curve x = 2 cos t, y = sin t + sin 2t to...Ch. 10.2 - (a) Find the slope of the tangent line to the...Ch. 10.2 - (a) Find the slope of the tangent to the astroid x...Ch. 10.2 - At what point(s) on the curve x = 3t2 + 1, y = t3 ...Ch. 10.2 - Find equations of the tangents to the curve x =...Ch. 10.2 - Use the parametric equations of an ellipse, x = a...Ch. 10.2 - Find the area enclosed by the curve x = t2 2t,...Ch. 10.2 - Find the area enclosed by the x-axis and the curve...Ch. 10.2 - Find the area of the region enclosed by the...Ch. 10.2 - Find the area under one arch of the trochoid of...Ch. 10.2 - Let R be the region enclosed by the loop of the...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Set up an integral that represents the length of...Ch. 10.2 - Find the exact length of the curve. 41. x = 1 +...Ch. 10.2 - Find the exact length of the curve. 42. x = et t,...Ch. 10.2 - Find the exact length of the curve. 43. x = t sin...Ch. 10.2 - Find the exact length of the curve. 44. x = 3 cos...Ch. 10.2 - Graph the curve and find its exact length. 45. x =...Ch. 10.2 - Graph the curve and find its exact length. 46....Ch. 10.2 - Graph the curve x = sin t + sin 1.5t, y = cos t...Ch. 10.2 - Find the length of the loop of the curve x = 3t ...Ch. 10.2 - Use Simpsons Rule with n = 6 to estimate the...Ch. 10.2 - In Exercise 10.1.43 you were asked to derive the...Ch. 10.2 - Find the distance traveled by a particle with...Ch. 10.2 - Find the distance traveled by a particle with...Ch. 10.2 - Show that the total length of the ellipse x = a...Ch. 10.2 - Find the total length of the astroid x = a cos3, y...Ch. 10.2 - (a) Graph the epitrochoid with equations...Ch. 10.2 - Set up an integral that represents the area of the...Ch. 10.2 - Set up an integral that represents the area of the...Ch. 10.2 - Set up an integral that represents the area of the...Ch. 10.2 - Set up an integral that represents the area of the...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Find the exact area of the surface obtained by...Ch. 10.2 - Graph the curve x=2coscos2y=2sinsin2 If this curve...Ch. 10.2 - Find the surface area generated by rotating the...Ch. 10.2 - Find the surface area generated by rotating the...Ch. 10.2 - If f is continuous and f(t) 0 for a t b, show...Ch. 10.2 - Use Formula 1 to derive Formula 6 from Formula...Ch. 10.2 - The curvature at a point P of a curve is defined...Ch. 10.2 - (a) Use the formula in Exercise 69(b) to find the...Ch. 10.2 - Use the formula in Exercise 69(a) to find the...Ch. 10.2 - (a) Show that the curvature at each point of a...Ch. 10.2 - A string is wound around a circle and then unwound...Ch. 10.2 - A cow is tied to a silo with radius r by a rope...Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - Plot the point whose polar coordinates are given....Ch. 10.3 - The Cartesian coordinates of a point are given....Ch. 10.3 - The Cartesian coordinates of a point are given....Ch. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Sketch the region in the plane consisting of...Ch. 10.3 - Find the distance between the points with polar...Ch. 10.3 - Find a formula for the distance between the points...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Identify the curve by finding a Cartesian equation...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - Find a polar equation for the curve represented by...Ch. 10.3 - For each of the described curves, decide if the...Ch. 10.3 - For each of the described curves, decide if the...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - Sketch the curve with the given polar equation by...Ch. 10.3 - The figure shows a graph of r as a function of in...Ch. 10.3 - The figure shows a graph of r as a function of in...Ch. 10.3 - Show that the polar curve r = 4 + 2 sec (called a...Ch. 10.3 - Show that the curve r = 2 csc (also a conchoid)...Ch. 10.3 - Show that the curve r = sin tan (called a...Ch. 10.3 - Sketch the curve (x2 + y2)3 = 4x2y2.Ch. 10.3 - (a) In Example 11 the graphs suggest that the...Ch. 10.3 - Match the polar equations with the graphs labeled...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the slope of the tangent line to the given...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Find the points on the given curve where the...Ch. 10.3 - Show that the polar equation r = a sin + b cos ,...Ch. 10.3 - Show that the curves r = a sin and r = a cos ...Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - Use a graphing device to graph the polar curve....Ch. 10.3 - How are the graphs of r = 1 + sin( /6) and r = 1...Ch. 10.3 - Use a graph to estimate the y-coordinate of the...Ch. 10.3 - Investigate the family of curves with polar...Ch. 10.3 - Investigate the family of polar curves r=1+cosn...Ch. 10.3 - Let P be any point (except the origin) on the...Ch. 10.3 - (a) Use Exercise 77 to show that the angle between...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the region that is bounded by the...Ch. 10.4 - Find the area of the shaded region. 5.Ch. 10.4 - Find the area of the shaded region. 6.Ch. 10.4 - Find the area of the shaded region. 7.Ch. 10.4 - Find the area of the shaded region. 8.Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Sketch the curve and find the area that it...Ch. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Graph the curve and find the area that it...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area of the region enclosed by one loop...Ch. 10.4 - Find the area enclosed by the loop of the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside the...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area of the region that lies inside both...Ch. 10.4 - Find the area inside the larger loop and outside...Ch. 10.4 - Find the area between a large loop and the...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - Find all points of intersection of the given...Ch. 10.4 - The points of intersection of the cardioid r = 1 +...Ch. 10.4 - When recording live performances, sound engineers...Ch. 10.4 - Find the exact length of the polar curve. 45. r =...Ch. 10.4 - Find the exact length of the polar curve. 46. r =...Ch. 10.4 - Find the exact length of the polar curve. 47. r =...Ch. 10.4 - Find the exact length of the polar curve. 48. r =...Ch. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Find the exact length of the curve. Use a graph to...Ch. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - Use a calculator to find the length of the curve...Ch. 10.4 - (a) Use Formula 10.2.6 to show that the area of...Ch. 10.4 - (a) Find a formula for the area of the surface...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find the vertex, focus, and directrix of the...Ch. 10.5 - Find an equation of the parabola. Then find the...Ch. 10.5 - Find an equation of the parabola. Then find the...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find the vertices and foci of the ellipse and...Ch. 10.5 - Find an equation of the ellipse. Then find its...Ch. 10.5 - Find an equation of the ellipse. Then find its...Ch. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Find the vertices, foci, and asymptotes of the...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Identify the type of conic section whose equation...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - Find an equation for the conic that satisfies the...Ch. 10.5 - The point in a lunar orbit nearest the surface of...Ch. 10.5 - A cross-section of a parabolic reflector is shown...Ch. 10.5 - The LORAN (LOng RAnge Navigation) radio navigation...Ch. 10.5 - Use the definition of a hyperbola to derive...Ch. 10.5 - Show that the function defined by the upper branch...Ch. 10.5 - Find an equation for the ellipse with foci (1, 1)...Ch. 10.5 - Determine the type of curve represented by the...Ch. 10.5 - (a) Show that the equation of the tangent line to...Ch. 10.5 - Show that the tangent lines to the parabola x2 =...Ch. 10.5 - Show that if an ellipse and a hyperbola have the...Ch. 10.5 - Use parametric equations and Simpsons Rule with n...Ch. 10.5 - The dwarf planet Pluto travels in an elliptical...Ch. 10.5 - Find the area of the region enclosed by the...Ch. 10.5 - (a) If an ellipse is rotated about its major axis,...Ch. 10.5 - Find the centroid of the region enclosed by the...Ch. 10.5 - (a) Calculate the surface area of the ellipsoid...Ch. 10.5 - Let P(x1, y1) be a point on the ellipse x2/a2 +...Ch. 10.5 - Let P(x1, y1) be a point on the hyperbola x2/a2 ...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - Write a polar equation of a conic with the focus...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity, (b) identify the conic,...Ch. 10.6 - (a) Find the eccentricity and directrix of the...Ch. 10.6 - Graph the conic r = 4/(5 + 6 cos ) and its...Ch. 10.6 - Graph the conics r = e/(1 e cos ) with e = 0.4,...Ch. 10.6 - (a) Graph the conics r = ed/(1 + e sin ) for e = 1...Ch. 10.6 - Show that a conic with focus at the origin,...Ch. 10.6 - Show that a conic with focus at the origin,...Ch. 10.6 - Show that a conic with focus at the origin,...Ch. 10.6 - Show that the parabolas r = c/(1 + cos ) and r =...Ch. 10.6 - The orbit of Mars around the sun is an ellipse...Ch. 10.6 - Jupiters orbit has eccentricity 0.048 and the...Ch. 10.6 - The orbit of Halleys comet, last seen in 1986 and...Ch. 10.6 - Comet Hale-Bopp, discovered in 1995, has an...Ch. 10.6 - The planet Mercury travels in an elliptical orbit...Ch. 10.6 - The distance from the dwarf planet Pluto to the...Ch. 10.6 - Using the data from Exercise 29, find the distance...Ch. 10 - (a) What is a parametric curve? (b) How do you...Ch. 10 - (a) How do you find the slope of a tangent to a...Ch. 10 - Write an expression for each of the following: (a)...Ch. 10 - (a) Use a diagram to explain the meaning of the...Ch. 10 - (a) How do you find the slope of a tangent line to...Ch. 10 - (a) Give a geometric definition of a parabola. (b)...Ch. 10 - (a) Give a definition of an ellipse in terms of...Ch. 10 - (a) Give a definition of a hyperbola in terms of...Ch. 10 - (a) What is the eccentricity of a conic section?...Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Determine whether the statement is true or false....Ch. 10 - Sketch the parametric curve and eliminate the...Ch. 10 - Sketch the parametric curve and eliminate the...Ch. 10 - Sketch the parametric curve and eliminate the...Ch. 10 - Sketch the parametric curve and eliminate the...Ch. 10 - Write three different sets of parametric equations...Ch. 10 - Use the graphs of x = f(t) and y = g(t) to sketch...Ch. 10 - (a) Plot the point with polar coordinates (4,...Ch. 10 - Sketch the region consisting of points whose polar...Ch. 10 - Sketch the polar curve. 9. r = 1 + sinCh. 10 - Sketch the polar curve. 10. r = sin 4Ch. 10 - Sketch the polar curve. 11. r = cos 3Ch. 10 - Sketch the polar curve. 12. r = 3 + cos 3Ch. 10 - Sketch the polar curve. 13. r = 1 + cos 2Ch. 10 - Sketch the polar curve. 14. r = 2 cos(/2)Ch. 10 - Sketch the polar curve. 15. r=31+2sinCh. 10 - Sketch the polar curve. 16. r=322cosCh. 10 - Find a polar equation for the curve represented by...Ch. 10 - Find a polar equation for the curve represented by...Ch. 10 - The curve with polar equation r = (sin )/ is...Ch. 10 - Graph the ellipse r = 2/(4 3 cos ) and its...Ch. 10 - Find the slope of the tangent line to the given...Ch. 10 - Find the slope of the tangent line to the given...Ch. 10 - Find the slope of the tangent line to the given...Ch. 10 - Find the slope of the tangent line to the given...Ch. 10 - Find dy/dx and d2y/dx2. 25. x = t + sin t, y = t ...Ch. 10 - Find dy/dx and d2y/dx2. 26. x = 1 + t2, y = t t3Ch. 10 - Use a graph to estimate the coordinates of the...Ch. 10 - Find the area enclosed by the loop of the curve in...Ch. 10 - At what points does the curve...Ch. 10 - Find the area enclosed by the curve in Exercise...Ch. 10 - Find the area enclosed by the curve r2 = 9 cos 5.Ch. 10 - Find the area enclosed by the inner loop of the...Ch. 10 - Find the points of intersection of the curves r =...Ch. 10 - Find the points of intersection of the curves r =...Ch. 10 - Find the area of the region that lies inside both...Ch. 10 - Find the area of the region that lies inside the...Ch. 10 - Find the length of the curve. 37. x = 3t2, y =...Ch. 10 - Find the length of the curve. 38. x = 2 + 3t, y =...Ch. 10 - Find the length of the curve. 39. r = 1/, 2Ch. 10 - Find the length of the curve. 40. r = sin3(/3), 0Ch. 10 - Find the area of the surface obtained by rotating...Ch. 10 - Find the area of the surface obtained by rotating...Ch. 10 - The curves defined by the parametric equations...Ch. 10 - A family of curves has polar equations ra = |sin...Ch. 10 - Find the foci and vertices and sketch the graph....Ch. 10 - Find the foci and vertices and sketch the graph....Ch. 10 - Find the foci and vertices and sketch the graph....Ch. 10 - Find the foci and vertices and sketch the graph....Ch. 10 - Find an equation of the ellipse with foci (4, 0)...Ch. 10 - Find an equation of the parabola with focus (2, 1)...Ch. 10 - Find an equation of the hyperbola with foci (0, 4)...Ch. 10 - Find an equation of the ellipse with foci (3, 2)...Ch. 10 - Find an equation for the ellipse that shares a...Ch. 10 - Show that if m is any real number, then there are...Ch. 10 - Find a polar equation for the ellipse with focus...Ch. 10 - Show that the angles between the polar axis and...Ch. 10 - In the figure the circle of radius a is...Ch. 10 - A curve called the folium of Descartes is defined...Ch. 10 - The outer circle in the figure has radius 1 and...Ch. 10 - (a) Find the highest and lowest points on the...Ch. 10 - What is the smallest viewing rectangle that...Ch. 10 - Four bugs are placed at the four comers of a...Ch. 10 - Show that any tangent line to a hyperbola touches...Ch. 10 - A circle C of radius 2r has its center at the...

Additional Math Textbook Solutions

Find more solutions based on key concepts
Finding x- and y-Intercepts In Exercises 2332, find the x- and y-intercepts of the graph of the equation. See E...

Calculus: An Applied Approach (MindTap Course List)

Logarithmic Properties What is the value of n? ln4+ln(n1)=ln4ln7

Calculus: Early Transcendental Functions

A poster is to have an area of 180 in2 with 1-inch margins at the bottom and sides and a 2-inch margin at the t...

Single Variable Calculus: Early Transcendentals, Volume I

In Exercises 9-14, decide whether the specified values come from a linear, quadratic, exponential, or absolute ...

Finite Mathematics and Applied Calculus (MindTap Course List)

Find the lengths of the medians of the triangle with vertices A(1, 0), B(3, 6), and C(8, 2). (A median is a lin...

Precalculus: Mathematics for Calculus (Standalone Book)

Convert the expressions in Exercises 8596 radical form. 0.2x2/3+37x1/2

Applied Calculus

Graph the function by hand, not by plotting points, but by starting with the graph of one of the standard funct...

Calculus: Early Transcendentals

There is some evidence that people with a visible tattoo are considered to be less attractive than are people w...

Essentials of Statistics for The Behavioral Sciences (MindTap Course List)

Distinguish between descriptive and inferential statistics. Describe a research situation that would use each t...

Essentials Of Statistics

Show that the polar equation r=asin+bcos, where ab0, represents a circle, and find its center and radius.

Calculus (MindTap Course List)

Oishi and Schimmk (2010) report that people who move from home to home frequently as children tend to have lowe...

Statistics for The Behavioral Sciences (MindTap Course List)

In Exercises 13-20, sketch a set of coordinate axes and plot each point. 16. (3, 4)

Applied Calculus for the Managerial, Life, and Social Sciences: A Brief Approach

For the function f whose graph is given, state the value of each quantity, if it exists. If it does not exist, ...

Single Variable Calculus

Evaluate expressions in Exercises 3756, rounding your answer to four significant digits where necessary. 14(1+1...

Finite Mathematics

Please provide the following information for Problems 11-22. part (a): (i) What is the level of significance? S...

Understanding Basic Statistics

For Problems 14-20, evaluate each algebraic expression for the given values of the variables. 2xyx+4y for x=3 a...

Intermediate Algebra

Let X be the number of packages being mailed by a randomly selected customer at a certain shipping facility. Su...

Probability and Statistics for Engineering and the Sciences

88 is what percent of 284? (to the nearest tenth)

Elementary Technical Mathematics

Difference of Sets Another operation that can be defined on sets A and B is the difference of the sets, denoted...

Mathematical Excursions (MindTap Course List)

Solve the following exercises by using tables. 17. Mary Evans plans to buy a used car when she starts college t...

Contemporary Mathematics for Business & Consumers

The perimeter of a triangle cannot have a measure that is twice the length of its longest side. HINT: Where a, ...

Elementary Geometry For College Students, 7e

Find the derivatives of the functions in Problems 1-34. 13.

Mathematical Applications for the Management, Life, and Social Sciences

Volume All edges of a cube are expanding at a rate of 6 centimeters per second. How fast is the volume changing...

Calculus: Early Transcendental Functions (MindTap Course List)

Find all values of a such that f is continuo us on : f(x)={x+1ifxax2ifxa

Single Variable Calculus: Early Transcendentals

Finding Values In Exercises 87-92, find the values of x for which the series converges. n=03(x4)n

Calculus of a Single Variable

In Exercise, Solve the systems of equations in. 12.

Elements Of Modern Algebra

Use a calculator to approximate csc(304o). a. 1.7883 b. 1.2062 c. 0.8290 d. 1.4826

Trigonometry (MindTap Course List)

f(x)=x+2x(x5) is continuous for all x except: a) x = 2 b) x = 2, 0, 5 c) x = 0, 5 d) f is continuous for all x.

Study Guide for Stewart's Single Variable Calculus: Early Transcendentals, 8th

For , f′(x) =

Study Guide for Stewart's Multivariable Calculus, 8th

In the Numbers Game, a state lottery, four numbers are drawn with replacement from an urn containing balls numb...

Finite Mathematics for the Managerial, Life, and Social Sciences

According to Reproductive Biology of the Aquatic Salamander Amphluma tridactylum in Louisiana (Journal of Herpe...

Introduction To Statistics And Data Analysis

In Exercises 9 to 28, use the drawings as needed to answer the following questions. Explain the difference, if ...

Elementary Geometry for College Students

Finding a Limit Graphically In Exercises 21-28, use the graph to find the limit (if it exists). If the limit do...

Calculus (MindTap Course List)

Finding a Limit In Exercises 83-90, find limx0f(x+x)f(x)x f(x)=3x2

Calculus

Finding a Magnitude of a VectorIn Exercises 1924, find the magnitude of v. v=24,7

Multivariable Calculus

Express each volume as indicated. Round each answer to the same number of significant digits as in the original...

Mathematics For Machine Technology

Describe how time, event, or individual sampling is done during behavioral observation, and explain why samplin...

Research Methods for the Behavioral Sciences (MindTap Course List)

To study the effect of temperature on yield in a chemical process, five batches were produced at each of three ...

Statistics for Business & Economics, Revised (MindTap Course List)

In working further with the problem of exercise 4, statisticians suggested the use of the following curvilinear...

STATISTICS F/BUSINESS+ECONOMICS-TEXT

Exercises 1-7 involve the information in Figure 9.113 on painting a room. What is the completion time? Task Len...

Mathematics: A Practical Odyssey

Explain how using college students as participants in a study may limit the external validity of a studys resea...

Research Methods for the Behavioral Sciences (MindTap Course List)

Evaluate each expression. k=1106

College Algebra (MindTap Course List)

Which of the following are second-order linear homogeneous recurrence relations with constant coefficients? a. ...

Discrete Mathematics With Applications

17. A national real estate company just acquired a smaller firm with 150 offices and 6000 agents in Los Angeles...

Modern Business Statistics with Microsoft Office Excel (with XLSTAT Education Edition Printed Access Card) (MindTap Course List)

In Problems 4548 without solving, match a solution curve of y + y = f(x) shown in the figure with one of the fo...

A First Course in Differential Equations with Modeling Applications (MindTap Course List)

For the following exercises, write the equation in equivalent logarithmic form. 263. 43/2=0.125

Calculus Volume 1

Using Quadratic Regression In Exercises S-13 through S-20, use regression to find a quadratic model for the giv...

Functions and Change: A Modeling Approach to College Algebra (MindTap Course List)

Athletic Shoe Sales. Skechers U.S.A., Inc., is a performance footwear company headquartered in Manhattan Beach,...

Essentials Of Statistics For Business & Economics

Use the following information to answer the next eleven exercises. The age of cars in the staff parking lot of ...

Introductory Statistics

Let Ln denote the left-endpoint sum using n subintervals and let Rn denote the corresponding right—endpoint sum...

Calculus Volume 2

Fill in the blanks. Radical expressions can be combined (added or subtracted) when they are .

College Algebra

bartleby
  • Contact Research (Essays)
  • High School Textbooks
  • Literature Guides
  • Essay Help
  • Mobile App
    • © 2021 bartleby. All Rights Reserved.