
Elementary Geometry for College Students
6th Edition
ISBN: 9781285195698
Author: Daniel C. Alexander, Geralyn M. Koeberlein
Publisher: Cengage Learning
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 11.2, Problem 41E
To determine
To find:
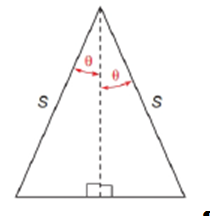
To show that the area of the isosceles
Expert Solution & Answer
Trending nowThis is a popular solution!

Chapter 11 Solutions
Elementary Geometry for College Students
Ch. 11.1 - In Exercises 1 to 6, find sin and sin for the...Ch. 11.1 - In Exercises 1 to 6, find sin and sin for the...Ch. 11.1 - In Exercises 1 to 6, find sin and sin for the...Ch. 11.1 - In Exercises 1 to 6, find sin and sin for the...Ch. 11.1 - In Exercises 1 to 6, find sin and sin for the...Ch. 11.1 - In Exercises 1 to 6, find sin and sin for the...Ch. 11.1 - In Exercises 7 to 14, use either Table 11.2 or a...Ch. 11.1 - In Exercises 7 to 14, use either Table 11.2 or a...Ch. 11.1 - Prob. 9ECh. 11.1 - Prob. 10E
Ch. 11.1 - In Exercises 7 to 14, use either Table 11.2 or a...Ch. 11.1 - Prob. 12ECh. 11.1 - Prob. 13ECh. 11.1 - Prob. 14ECh. 11.1 - In Exercises 15 to 20, find the lengths of the...Ch. 11.1 - In Exercises 15 to 20, find the lengths of the...Ch. 11.1 - Prob. 17ECh. 11.1 - In Exercises 15 to 20, find the lengths of the...Ch. 11.1 - In Exercises 15 to 20, find the lengths of the...Ch. 11.1 - Prob. 20ECh. 11.1 - In Exercises 21 to 26, find the measures of the...Ch. 11.1 - Prob. 22ECh. 11.1 - In Exercises 21 to 26, find the measures of the...Ch. 11.1 - Prob. 24ECh. 11.1 - In Exercises 21 to 26, find the measures of the...Ch. 11.1 - Prob. 26ECh. 11.1 - In Exercises 27 to 34, use the drawings, where...Ch. 11.1 - In Exercises 27 to 34, use the drawings, where...Ch. 11.1 - Prob. 29ECh. 11.1 - Prob. 30ECh. 11.1 - Prob. 31ECh. 11.1 - In Exercises 27 to 34, use the drawings, where...Ch. 11.1 - Prob. 33ECh. 11.1 - In Exercises 27 to 34, use the drawings, where...Ch. 11.1 - Prob. 35ECh. 11.1 - Prob. 36ECh. 11.1 - For Exercises 35 to 38, make drawings as needed....Ch. 11.1 - Prob. 38ECh. 11.1 - Prob. 39ECh. 11.2 - In Exercises 1 to 6, find cos and cos.Ch. 11.2 - In Exercises 1 to 6, find cos and cos.Ch. 11.2 - Prob. 3ECh. 11.2 - Prob. 4ECh. 11.2 - In Exercises 1 to 6, find cos and cos.Ch. 11.2 - Prob. 6ECh. 11.2 - Prob. 7ECh. 11.2 - Prob. 8ECh. 11.2 - Prob. 9ECh. 11.2 - Prob. 10ECh. 11.2 - Prob. 11ECh. 11.2 - Prob. 12ECh. 11.2 - Prob. 13ECh. 11.2 - Prob. 14ECh. 11.2 - Prob. 15ECh. 11.2 - Prob. 16ECh. 11.2 - In Exercise 17 to 22, use either the sine ratio or...Ch. 11.2 - In Exercise 17 to 22, use either the sine ratio or...Ch. 11.2 - Prob. 19ECh. 11.2 - Prob. 20ECh. 11.2 - Prob. 21ECh. 11.2 - In Exercise 17 to 22, use either the sine ratio or...Ch. 11.2 - In Exercise 23 to 28, use either the sine ratio or...Ch. 11.2 - In Exercise 23 to 28, use either the sine ratio or...Ch. 11.2 - Prob. 25ECh. 11.2 - Prob. 26ECh. 11.2 - Prob. 27ECh. 11.2 - Prob. 28ECh. 11.2 - Prob. 29ECh. 11.2 - Prob. 30ECh. 11.2 - Prob. 31ECh. 11.2 - Prob. 32ECh. 11.2 - In Exercise 29 to 37, angle measures should be...Ch. 11.2 - Prob. 34ECh. 11.2 - Prob. 35ECh. 11.2 - In Exercise 29 to 37, angle measures should be...Ch. 11.2 - Prob. 37ECh. 11.2 - Prob. 38ECh. 11.2 - Prob. 39ECh. 11.2 - Prob. 40ECh. 11.2 - Prob. 41ECh. 11.2 - For Exercise 42 and 43, use the drawing and the...Ch. 11.2 - Prob. 43ECh. 11.2 - Prob. 44ECh. 11.2 - Prob. 45ECh. 11.3 - In Exercises 1 to 4, find tan and tan for each...Ch. 11.3 - In Exercises 1 to 4, find tan and tan for each...Ch. 11.3 - In Exercises 1 to 4, find tan and tan for each...Ch. 11.3 - Prob. 4ECh. 11.3 - In Exercises 5 to 10, find the value or expression...Ch. 11.3 - In Exercises 5 to 10, find the value or expression...Ch. 11.3 - In Exercises 5 to 10, find the value or expression...Ch. 11.3 - Prob. 8ECh. 11.3 - Prob. 9ECh. 11.3 - Prob. 10ECh. 11.3 - Prob. 11ECh. 11.3 - Prob. 12ECh. 11.3 - Prob. 13ECh. 11.3 - Prob. 14ECh. 11.3 - Prob. 15ECh. 11.3 - Prob. 16ECh. 11.3 - Prob. 17ECh. 11.3 - Prob. 18ECh. 11.3 - In Exercises 15 to 20, use the sine, cosine, or...Ch. 11.3 - In Exercises 15 to 20, use the sine, cosine, or...Ch. 11.3 - Prob. 21ECh. 11.3 - In Exercises 21 to 26, use the sine, cosine, or...Ch. 11.3 - In Exercises 21 to 26, use the sine, cosine, or...Ch. 11.3 - Prob. 24ECh. 11.3 - In Exercises 21 to 26, use the sine, cosine, or...Ch. 11.3 - Prob. 26ECh. 11.3 - Prob. 27ECh. 11.3 - Prob. 28ECh. 11.3 - In Exercises 27 to 32, use a calculator and...Ch. 11.3 - Prob. 30ECh. 11.3 - Prob. 31ECh. 11.3 - Prob. 32ECh. 11.3 - Prob. 33ECh. 11.3 - Prob. 34ECh. 11.3 - Prob. 35ECh. 11.3 - Prob. 36ECh. 11.3 - Prob. 37ECh. 11.3 - Prob. 38ECh. 11.3 - Prob. 39ECh. 11.3 - Prob. 40ECh. 11.3 - Prob. 41ECh. 11.3 - In Exercises 37 to 43, angle measures should be...Ch. 11.3 - In Exercises 37 to 43, angle measures should be...Ch. 11.3 - Prob. 44ECh. 11.3 - Prob. 45ECh. 11.3 - Prob. 46ECh. 11.3 - Prob. 47ECh. 11.4 - In Exercises 1 and 2, use the given information to...Ch. 11.4 - Prob. 2ECh. 11.4 - Prob. 3ECh. 11.4 - In Exercises 3 and 4, state the form of the Law of...Ch. 11.4 - Prob. 5ECh. 11.4 - Prob. 6ECh. 11.4 - Prob. 7ECh. 11.4 - Prob. 8ECh. 11.4 - Prob. 9ECh. 11.4 - Prob. 10ECh. 11.4 - Prob. 11ECh. 11.4 - Prob. 12ECh. 11.4 - Prob. 13ECh. 11.4 - Prob. 14ECh. 11.4 - Prob. 15ECh. 11.4 - In Exercises 15 and 16, find the area of the given...Ch. 11.4 - Prob. 17ECh. 11.4 - Prob. 18ECh. 11.4 - Prob. 19ECh. 11.4 - Prob. 20ECh. 11.4 - Prob. 21ECh. 11.4 - Prob. 22ECh. 11.4 - Prob. 23ECh. 11.4 - Prob. 24ECh. 11.4 - Prob. 25ECh. 11.4 - Prob. 26ECh. 11.4 - Prob. 27ECh. 11.4 - Prob. 28ECh. 11.4 - Prob. 29ECh. 11.4 - Prob. 30ECh. 11.4 - In Exercises 29 to 34, use the Law of Sines or the...Ch. 11.4 - Prob. 32ECh. 11.4 - Prob. 33ECh. 11.4 - Prob. 34ECh. 11.4 - Prob. 35ECh. 11.4 - Prob. 36ECh. 11.4 - Prob. 37ECh. 11.4 - Show that the form of the Law of Cosines written...Ch. 11.4 - Explain why the area of the parallelogram shown is...Ch. 11.4 - Prob. 40ECh. 11.4 - Prob. 41ECh. 11.4 - Prob. 42ECh. 11.4 - Prob. 43ECh. 11.4 - Prob. 44ECh. 11.CR - In Exercises 1 to 4, state the ratio needed, and...Ch. 11.CR - In Exercises 1 to 4, state the ratio needed, and...Ch. 11.CR - In Exercises 1 to 4, state the ratio needed, and...Ch. 11.CR - Prob. 4CRCh. 11.CR - In Exercises 5 to 8, state the ratio needed, and...Ch. 11.CR - In Exercises 5 to 8, state the ratio needed, and...Ch. 11.CR - In Exercises 5 to 8, state the ratio needed, and...Ch. 11.CR - In Exercises 5 to 8, state the ratio needed, and...Ch. 11.CR - In Exercises 9 to 12, use the Law of Sines or the...Ch. 11.CR - Prob. 10CRCh. 11.CR - In Exercises 9 to 12, use the Law of Sines or the...Ch. 11.CR - Prob. 12CRCh. 11.CR - Prob. 13CRCh. 11.CR - Prob. 14CRCh. 11.CR - Prob. 15CRCh. 11.CR - Prob. 16CRCh. 11.CR - Prob. 17CRCh. 11.CR - Prob. 18CRCh. 11.CR - Prob. 19CRCh. 11.CR - Prob. 20CRCh. 11.CR - In exercises 21 to 30. Use the drawings. Where...Ch. 11.CR - In exercises 21 to 30. Use the drawings. Where...Ch. 11.CR - In exercises 21 to 30. Use the drawings. Where...Ch. 11.CR - In Exercises 21 to 30, use the drawings, where...Ch. 11.CR - Prob. 25CRCh. 11.CR - Prob. 26CRCh. 11.CR - Prob. 27CRCh. 11.CR - Prob. 28CRCh. 11.CR - Prob. 29CRCh. 11.CR - In Exercises 21 to 30, use the drawings, where...Ch. 11.CR - Prob. 31CRCh. 11.CR - Prob. 32CRCh. 11.CR - Prob. 33CRCh. 11.CR - Prob. 34CRCh. 11.CT - Prob. 1CTCh. 11.CT - Prob. 2CTCh. 11.CT - Prob. 3CTCh. 11.CT - Prob. 4CTCh. 11.CT - Using your calculator, find to the nearest degree...Ch. 11.CT - Without the calculator, determine which number is...Ch. 11.CT - Prob. 7CTCh. 11.CT - Prob. 8CTCh. 11.CT - Prob. 9CTCh. 11.CT - Prob. 10CTCh. 11.CT - Prob. 11CTCh. 11.CT - Prob. 12CTCh. 11.CT - Prob. 13CTCh. 11.CT - Prob. 14CTCh. 11.CT - Prob. 15CTCh. 11.CT - Prob. 16CTCh. 11.CT - Prob. 17CTCh. 11.CT - Prob. 18CTCh. 11.CT - Prob. 19CTCh. 11.CT - Prob. 20CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- A central angle is drawn in a circle of radius r, as in the figure below. a The length of the arc subtended by is s = ________. b The area of the sector with central angle is A =________.arrow_forwardLet Px,y be the terminal points on the unit circle determined by t. Then sin t =____, cos t =_____ and tan t =________.arrow_forwardA point that moves on a coordinate line is in simple when its distance d from the origin at time t is given by either d=asintord=acost.arrow_forward
arrow_back_ios
arrow_forward_ios
Recommended textbooks for you
 Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary Geometry For College Students, 7eGeometryISBN:9781337614085Author:Alexander, Daniel C.; Koeberlein, Geralyn M.Publisher:Cengage,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning

Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,

Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage

Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning

Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Trigonometric Ratios; Author: The Organic Chemistry Tutor;https://www.youtube.com/watch?v=9-eHMMpQC2k;License: Standard YouTube License, CC-BY