
Concept explainers
Suppose that a scientist has reason to believe that two quantities x and y are related linearly, that is, y = mx + b, at least approximately, for some values of m and b. The scientist performs an experiment and collects data in the form of points (x1, x2), (x2, y2) ,…, (xn, yn) and then plots these points. The points don’t lie exactly on a straight line, so the scientist wants to find constants m and b so that the line y = mx + b “fits” the points as well as possible (see the figure).
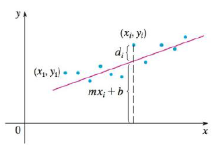
Let di = yi − (mxi, + b) be the vertical deviation of the point (xi, yi) from the line. The method of least squares determines m and b so as to minimize
and
Trending nowThis is a popular solution!

Chapter 14 Solutions
Multivariable Calculus
- For which values of t is each set linearly independent? a S={(t,0,0),(0,1,0),(0,0,1)} b S={(t,t,t),(t,1,0),(t,0,1)}arrow_forwardShow that the three points (x1,y1)(x2,y2) and (x3,y3) in the a plane are collinear if and only if the matrix [x1y11x2y21x3y31] has rank less than 3.arrow_forwardUse a software program or a graphing utility to write v as a linear combination of u1, u2, u3, u4, u5 and u6. Then verify your solution. v=(10,30,13,14,7,27) u1=(1,2,3,4,1,2) u2=(1,2,1,1,2,1) u3=(0,2,1,2,1,1) u4=(1,0,3,4,1,2) u5=(1,2,1,1,2,3) u6=(3,2,1,2,3,0)arrow_forward
 Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage LearningAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning


