
An analysis of a circuit shown in Fig. P2.1 yields the
(a) Rewrite the above equation in the form
(b) Solve the equation in part (a) by each of the following methods: factoring, compacting the square, and the quadratic formula.
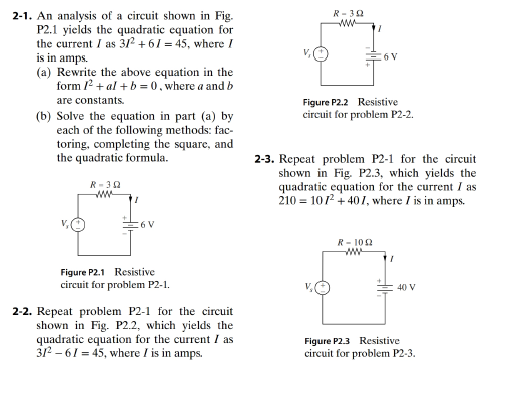
(a)
To rewrite the given current relation in the form of
Answer to Problem 1P
The required equation of current in the form of
Explanation of Solution
Given:
The current relation is given as
Calculation:
Divide by
Rearrange above equation.
The required equation of current in the form of
Conclusion:
Thus, the required equation of current in the form of
(b)
Solve the equation
Answer to Problem 1P
The equation is solved by factoring, completing the square, and the quadratic and the roots of the equation are
Explanation of Solution
Concept Used:
The roots of the quadratic equation can be determined by the quadratic formula given as-
Calculation:
Substitute
This equation gives two values of current
For completing square method,
Rearrange equation (1)
Add
Rearrange the above equation.
The value of current
For factoring method,
Rearrange equation (1)
The value of current
Want to see more full solutions like this?
Chapter 2 Solutions
Introductory Mathematics for Engineering Applications
Additional Math Textbook Solutions
Basic Technical Mathematics
Advanced Engineering Mathematics
Fundamentals of Differential Equations (9th Edition)
Finite Mathematics for Business, Economics, Life Sciences and Social Sciences
Basic Business Statistics, Student Value Edition (13th Edition)
Probability and Statistics for Engineering and the Sciences
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
